Quaternary antiferromagnetic Ba2BiFeS5 with isolated FeS4 tetrahedra

Shaohua Wang(王少华), Xiao Zhang(张晓), and Hechang Lei(雷和畅),†

1Department of Physics and Beijing Key Laboratory of Opto-electronic Functional Materials&Micro-nano Devices,Renmin University of China,Beijing 100872,China

2State Key Laboratory of Information Photonics and Optical Communications&School of Science,Beijing University of Posts and Telecommunications,Beijing 100876,China

Keywords: isolated FeS4 tetrahedra,antiferromagnetic transition,short-range antiferromagnetic fluctuation

1. Introduction

The discovery of iron-based superconductors promotes the development of studies on iron-based materials.[1-6]In the past decade, different kinds of iron-based compounds are reported and they can be classified according to the dimensionality of structural unit formed by the FeX4(X =pnictogens and chalcogens) tetrahedra. Most of ironbased superconductors, such as LaOFeAs, BaFe2As2, FeSe,(Li1-xFex)OHFeSe,and Lix(NH3)yFe2Se2,[1,2,6-9]share common two-dimensional (2D) FeX layers built up with edgesharing FeX4tetrahedra.[10]When FeX4tetrahedra connect each other along one crystallographic axis via edge sharing,they can form quasi-one-dimensional (quasi-1D) compounds such as KFeS2with single 1D FeS4chain along the c axis,[11]BaFe2S3and BaFe2Se3with double 1D FeS4or FeSe4chains(spin-ladder structure)along the b axis.[12-14]The latter compounds exhibit Mott insulating behaviors with antiferromagnetic (AFM) orders at ambient pressure.[12-14]Interestingly,both of BaFe2S3and BaFe2Se3show superconductivity under pressure.[15-17]Moreover, the connected edge-sharing FeX4tetrahedra can also form three-dimensional (3D) compounds like CaFe4As3.[18]It displays non-Fermi-liquid behavior at zero field with enhanced electron-electron correlations.[18]Thus, exploration of iron-based compounds with various dimensionality of FeX4units would provide a comprehensive understanding of the relation between electronic correlation and dimensionality in the iron-based materials.

When compared to the extensively studied ternary compounds, the studies on quaternary iron-based compounds are still rare so far. Recently, the quaternary compounds Ba2PnFeCh5(Pn = Sb, Bi, and Ch = S, Se) containing isolated (zero-dimensional, 0D) FeCh4tetrahedra are reported.[19-21]Previous studies indicate that they exhibit AFM order at low temperature in general.[19-21]In this work,we have grown the single crystal of Ba2BiFeS5and carried out a detailed study on physical properties. It shows a long-range AFM order with Neel temperature TN∼30 K,and there may be an AFM fluctuation before the formation of longe-range antiferromagnetism.

2. Experiment

Single crystals of Ba2BiFeS5were grown by solid state reaction method. Ba pieces (99.9%), Bi shots (99.99%), Fe lumps (99.98%), and S granules (99.999%) were mixed with a stoichiometric molar ratio Ba:Bi:Fe:S=2:1:1:5. The mixture was loaded in an alumina crucible which was put into a quartz tube. These operations were handled in the glovebox with the O2and H2O contents under 0.1 ppm. Then the quartz tube was sealed with Ar gas under the pressure of 0.2 atmospheres. The sealed tube was heated up to 1273 K for 24 h and kept at 1273 K for 48 h. Then it was cooled down to 673 K with 3 K/h before finally switching off the furnace. The crystals can be extracted from the matrix mechanically. X-ray diffraction (XRD) patterns were collected using a Bruker D8 X-ray Diffractometer with Cu Kαradiation (λ =1.5418 ˚A) at room temperature. The lattice pa-rameters were obtained by fitting the powder XRD pattern using the TOPAS4 software.[22]The elemental analysis was performed using an energy-dispersive x-ray spectroscopy(EDX)in a JEOL JSM-6500 scanning electron microscope. Magnetization measurements were performed in a Quantum Design Magnetic Property Measurement System(MPMS3).Heat capacity measurements were performed in Quantum Design PPMS-14.

3. Results and discussion

Figure 1(a) shows the structure of Ba2BiFeS5. The structure is formed by alternatively stacking Fe-Bi-S layers and Ba2+cations along the a axis. The main building blocks of a Fe-Bi-S layer in the bc plane are FeS4tetrahedra and BiS5quadrangular pyramids. As shown in Fig. 1(b), the 1D connected chain of BiS5along the b axis consists of edge-sharing BiS5quadrangular pyramids. Via edge sharing, FeS4tetrahedra connect on both sides of this chain along the c axis alternatively with the atomic distance dFe-Bi= 3.264 ˚A. On the other hand, the shortest atomic distance between two Fe ions in the neighboring Fe-Bi-S chains is very large (∼5.8 ˚A), comparable with the interchain distance of Fe ions in BaFe2S3(∼5.86 ˚A).[12]Thus,FeS4tetrahedron in Ba2BiFeS5can be viewed as a 0D unit.Figure 1(c) shows the powder x-ray diffraction pattern of the ground crystals and it is found that this pattern can be well fitted by the Rietveld method using the reported structure of Ba2BiFeS5(space group Pnma) with minor second phase BaBi2S4(∼6.9(1) wt%). It is hard to eliminate the minority phase of BaBi2S4because it is very stable and its formation temperature overlaps with Ba2BiFeS5.[23]The refined lattice parameters are a=12.1378(7) ˚A, b=8.9419(4) ˚A, and c=8.8294(5) ˚A.These values are close to previous results[19]but slightly smaller than those in Ba2BiFeSe5,[20,21]which can be ascribed to the smaller ionic size of S than Se. The analysis of EDX result shown in Fig. 1(d) confirms the existence of Ba, Bi, Fe, and S. The obtained ratio of Ba:Bi:Fe:S is 2.17(3):0.99(6):1:5.34(3)when setting the content of Fe as 1, consistent with the chemical formula of Ba2BiFeS5. The inset of Fig. 1(d) displays the photograph of typical crystals of Ba2BiFeS5. They have a sub-millimeter size with black color. The subquadrate shape is in agreement with the crystallographic symmetry of Ba2BiFeS5.

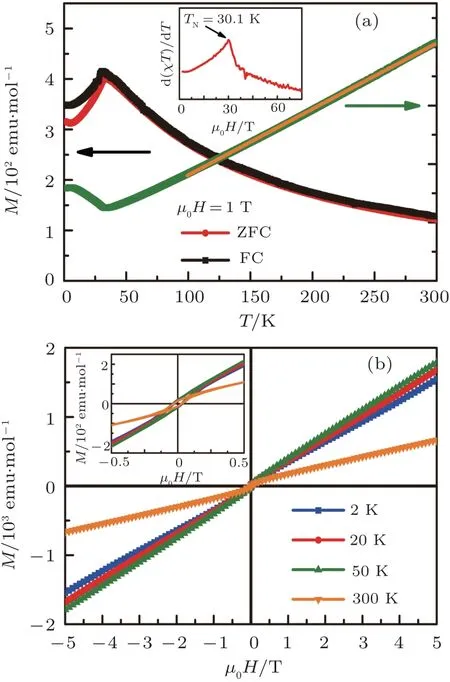
Fig.2. (a) Temperature dependence of magnetization M(T)from 1.8 K to 300 K with the zero-field cooling (ZFC) and the field cooling (FC) modes and the Curie-Weiss fitting of temperature dependence of inverse magnetic susceptibility 1/χ(T) (orange solid line). Inset: d(χT)/dT as a function of T. (b) Isothermal magnetization hysteresis loops M(µ0H) in the field range from-5 T to 5 T at various temperatures. Inset: the enlarged part of M(µ0H)curves at low-field region.

Temperature dependence of magnetization M(T)for several pieces of Ba2BiFeS5crystals at µ0H =1 T is shown in Fig. 2(a). It can be seen that the M(T) increases as the temperature decreases from 300 K to 35 K.There is a sudden drop when lowering temperature further,suggesting that there is an AFM transition in Ba2BiFeS5. The determined AFM transition temperature TNfrom the peak of d(χT)/dT curve with zero-field cooling mode is 30.1 K (the inset of Fig. 2(a)),[24]which is consistent with the pervious report.[19]When T ＜TN,there is a similar drop in the field-cooling (FC) M(T) curve,implying the absence of magnetic glassy state.When T ＜6 K,there are upturns appearing in both ZFC and FC M(T)curves,possibly due to the contribution of minor impurities in the sample. For T ＞TN, the inverse of magnetic susceptibility 1/χ(T) exhibits the nearly linear behavior up to 300 K(Fig.2(a)).It can be fitted very well using the Curie-Weiss law χ(T)=C/(T-θ),where C is the Curie constant and θ is the Weiss temperature. The linear fit of 1/χ(T) between 100 K and 300 K with ZFC mode(orange solid line in Fig.2(a))gives C=4.42(5)emu·g-1·Oe-1·K and θ =-60.27(6)K,indicating the dominant AFM interaction in this material.It is also in agreement with the AFM ordering below TN. The value of C corresponds to the effective moment µeff=5.94(3)µB/Fe,close to the expected local moment of high-spin Fe3+ion(S=5/2,spin-onlyµeff=5.92µB/Fe).Compared to isostructural Ba2BiFeSe5with larger TN∼79 K, the shortest Fe-Fe distance in Ba2BiFeS5(5.864 ˚A) is shorter than that in Ba2BiFeSe5(6.0 ˚A),[21]indicating the direct magnetic interactions may not be dominant. Meanwhile,band structure calculations show that Ba2BiFeS5is an insulator with no conduction electron,[19]so that the RKKY interaction is excluded.Thus one of the possible magnetic interacting mechanisms is superexchanging interaction,i.e.,Fe atoms interact with each other via Bi and/or S atoms.[21]Figure 2(b) shows the field dependence of magnetization M(H) at various temperatures.The M(H) loops exhibit the almost linear behaviors without the trend of saturation,irrespective of temperatures,consistent with the feature of AFM transition in Ba2BiFeS5. It has to be noted that there is a small hysteresis at low-field region for all of curves, even when T ＞TN. This could originate from the minor ferromagnetic impurities in the sample.

The specific heat capacity Cp(T)measurement from 2 K to 150 K is presented in Fig. 3(a). An anomalous behavior can be obviously observed at 31.3 K, corresponding to the long-range AFM transition. The TNobtained from the peak in Cp(T) curve is close to that derived from the d(χT)/dT curve in the inset of Fig. 2(a). Because of the AFM insulator feature of Ba2BiFeS5,[19]the total specific heat capacity can be divided into lattice(Cph)and magnetic(Cm)parts. The Cphcan be fitted using the 5th polynomial between temperature range of 2 K-10 K and 70 K-100 K (red solid line in Fig.3(a)). This method has been adopted in previous reports to estimate the heat capacity of lattice vibration.[25-27]After subtracting the lattice contribution,the obtained Cm(T)is presented in Fig. 3(b) (green symbols). There is a peak shown in Cm(T) curve, corresponding to the paramagnetic (PM) to AFM transition.

Magnetic entropy Sm(T)can be calculated by integrating the Cm/T. The derived temperature dependence of Sm(T) is shown in Fig. 3(b)(orange solid line). It can be seen that the Sm(T)is small when T is far below TN. However,it increases dramatically when T is approaching TNbecause of the significant release of magnetic entropy at PM-AFM traction. Finally,it becomes saturated at higher temperature. The value of Smat 100 K is 6.6 J·mol-1·K-1,which is much smaller than theoretical value Rln(2S+1)=14.9 J·mol-1·K-1for highspin Fe3+ion with S =5/2 (brown dashed line, Fig. 3(b)).One of the possible reasons is the existing of short range magnetic fluctuation above TN, partially reflecting from the difference between the θ and TN. The overestimation of Cphwould be another reason causing the smaller values of Cmand corresponding Smthan actual ones. On the other hand, assuming the neglible contribution of Cm(T)at low temperature(T ＜10 K), the Cp(T) can be well fitted using the formula Cp/T =βT2(inset of Fig.3(a)). The value of coefficient related to the phonon contribution β is 4.85(9)mJ·mol-1·K-4and the calculated Debye temperature is ΘD=153(3)K using the formula ΘD=(12π4NR/5β)1/3, where N is the atomic number in the chemical formula(N=9)and R is the gas constant (R=8.314 J·mol-1K-1). It should be noted that the derived ΘDfrom fitted β has some uncertainty because the temperature dependence of heat capacity for antiferromagnetic magnons excitation also follow the T3behavior.

Fig.3. (a)Temperature dependence of heat capacity Cp(T)for Ba2BiFeS5 single crystal at zero field. The red solid curve represents the lattice contribution, fitted by a polynomial. Inset: enlarged part at low temperature region. The red solid line is the fit using the formula Cp(T)/T =βT2. (b)Temperature dependence of Cm(T) (left label, green symbols) and Sm(T)curves(right label,orange solid line). The brown dashed line represents the theoretical value of Sm (Rln6 for S=5/2 system).

4. Conclusion

In summary, we grew single crystal of Ba2BiFeS5containing 0D structural unit of FeS4tetrahedra. The fti of hightemperature M(T)curve using the Curie-Weiss law gives theµeff=5.94(3)µB/Fe,indicating that the Fe3+ions in this compound are at the high-spin state(S=5/2). Moreover,the negative value of θ (∼-60 K) suggests the dominant AFM interaction. The long-range AFM order forms at TN∼30 K,confirmed by both magnetization and heat capacity measurements. By analyzing the Cm(T), we find that the Smat TN(4.79 J·mol-1K-1)is much smaller than the theoretical value for high-spin state Fe3+ions(14.9 J·mol-1·K-1). It might be ascribed to the short-range antiferromagnetic fluctuation above TNor the overestimated phonon contribution to heat capacity.