某人行天桥计算模型对比分析

马 悦 杨海平 谢圣纲

（重庆市设计院，重庆 400039 ）

1 工程概况

本工程位于江北观音桥商圈环道银鑫菜市场的T字型交叉路口段，设计范围为该路段的人行过街系统设计，经分析研究后确定为人行天桥。天桥长63.5 m，宽4 m，为钢箱梁结构人行天桥，桥梁平面布置如图1所示。

图1 桥梁平面布置图

现因景观改造，该人行天桥拟铲除原有面层后，采用花岗岩面层重铺桥面，拆除两侧栏杆后在两侧重新设置玻璃栏杆，并在人行天桥一侧安装路灯，在天桥两侧安装种植花草装饰。主要变更的荷载情况为花岗石面层恒载标准值1.55 kN/m2，种植花草装饰恒载标准值2.31 kN/m2，路灯恒载0.8 kN/个。改造前的人行天桥现状情况如图2所示。

图2 改造前人行天桥现状示意图

2 人行天桥的计算结果分析

钢箱梁桥体和钢筋混凝土柱是一种成熟的人行天桥设计方案，相关人员对此提供了充足的理论支持和实践研究[1-5]。但是，桥梁博士V4.0作为一种较新的计算软件，在过往常用的桥梁博士V3.0的基础上有较大变化，其建模过程中各参数的取值和计算结果的可靠性仍需要大量实例的验证。同时，如果在建模过程中对梯道梁等部件采用了简化处理，将对计算结果产生未知的影响。有鉴于此，本文分别在桥梁博士中建立了无梯道模型、梯道转换为荷载模型和含梯道模型，在Midas Civil中建立了含梯道模型，对比了不同计算软件中计算结果的差异，分析了模型简化程度对计算结果的影响。

2.1 模型简化对人行天桥计算结果影响的对比分析

典型的无梯道模型和含梯道模型的运营阶段标准组合竖弯矩My内力组合包络图如图3所示。

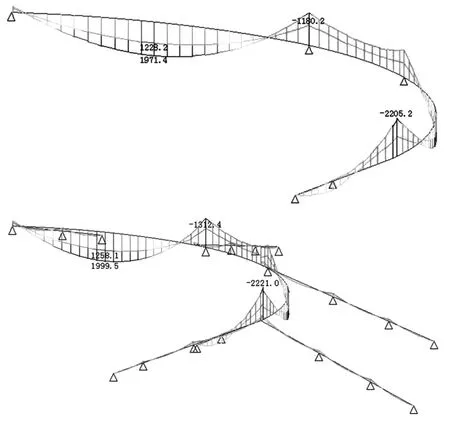
图3 无梯道模型和含梯道模型运营阶段标准组合竖弯矩My内力组合包络图

将三种人行天桥模型的标准组合节点位移包络值汇总，可以得到无梯道模型、梯道转换为荷载模型和含梯道模型的运营阶段标准组合竖弯矩My内力组合包络值对比表如表1所示。

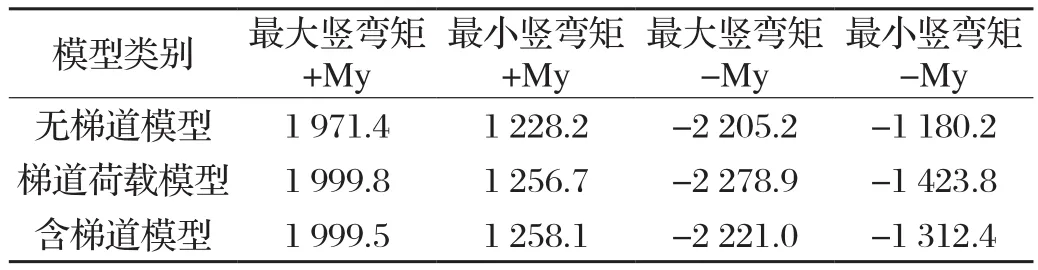
表1 运营阶段标准组合竖弯矩My内力组合包络值对比表

同时，在钢箱梁上取三个应力点，得到三种模型中不同应力点的最大应力值和最小应力值对比表如表2所示。

表2 运营阶段标准组合应力包络值对比表

从上述数据可以看到，无梯道模型的内力包络值计算结果最大偏差达到了11.2%，梯道转换为荷载模型的应力值计算结果最大偏差达到了15.9%，说明如果对梯道梁等部件采用了简化处理，将对计算结果产生明显影响。

典型的无梯道模型和含梯道模型的标准组合节点位移包络图如图4所示。

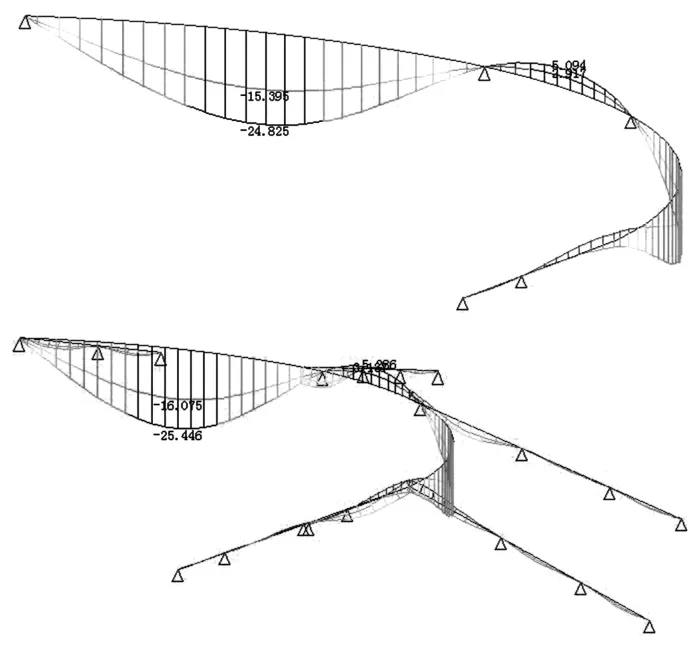
图4 无梯道模型和含梯道模型标准组合节点位移包络图

将三种人行天桥模型的标准组合节点位移包络值汇总，可以得到无梯道模型、梯道转换为荷载模型和含梯道模型的标准组合节点位移包络值对比表如表3所示。

将两种人行天桥模型的竖向主振型模态和频率值汇总，可以得到无梯道模型和含梯道模型的竖向主振型模态和频率值对比表如表4所示。

从上述结果可以看出，当将梯道梁简化为荷载加载在主梁上时，人行天桥的周期和频率计算结果有较大变化，而频率是人行天桥设计时的重要指标之一，因此，应在模型中考虑人行天桥梯道梁的影响。

2.2 不同计算软件的对比分析

为判断有限元计算模型计算的准确性，采用Midas Civil和桥梁博士4.0分别建立有限元模型，并对计算结果进行了对比，两种有限元软件所建立的有限元模型对比图如图5所示。

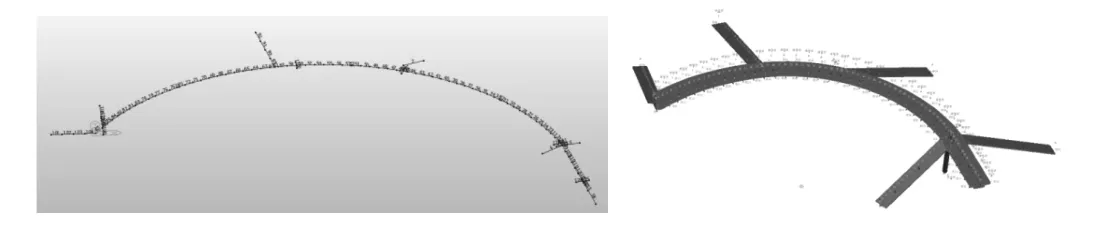
图5 Midas Civil和桥梁博士V4.0的有限元模型对比图

两种有限元模型的自重内力计算结果对比图如图6所示。

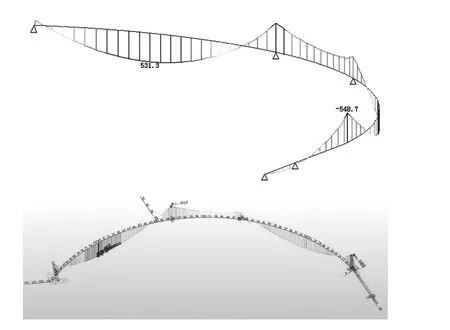
图6 Midas和桥梁博士的自重内力计算结果对比图

上述计算结果表明，两种有限元模型在自重影响下的内力情况具有足够的相似性，可以作为后续分析的依据。

两种有限元模型的运营阶段内力计算结果如表5所示。

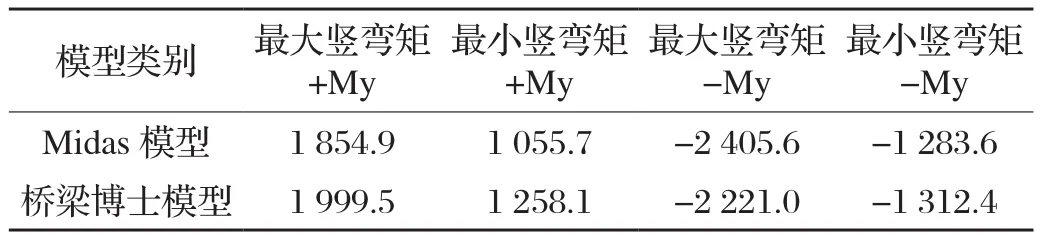
表5 运营阶段标准组合竖弯矩My内力组合包络值对比表

上述计算结果表明，因为模型建立、荷载添加等方面的差异，导致Midas Civil和桥梁博士V4.0在计算结果上存在一定的不同。

3 结语

（1） 桥梁博士V4.0与Midas Civil的计算结果对比表明，该软件对钢箱梁人行天桥的计算结果比较可靠。

（2） 桥梁博士V4.0与以前常用的桥梁博士V3.0在模型建立、荷载添加等方面均具有较大的差异，为保证建模过程的准确性，建议在前期适应阶段采用Midas Civil等软件进行计算结果的对比验证。

（3） 在建模时是否考虑梯道梁或者等效荷载，对人行天桥的计算结果具有明显的影响。