云计算调度粒子群改进算法①

罗 云,唐丽晴

(武警海警学院 计算机教研室,宁波 315801)

引言

云计算环境中存在着诸多不同类型的计算资源,各种类型的资源之间存在着一定的差异.云计算资源调度问题正是将云环境中的各类资源进行合理调度,以达到缩短计算时间且提高资源利用率等目的的复杂调度问题.随着“互联网+”和“自媒体”概念的日益升温,长期以来被应用的调度效率较低的云计算资源调度算法不再能够满足人们的现实需求[1].

云计算资源调度算法研究已成为云计算领域的研究热点之一.云计算资源调度需要同时兼顾计算效率和负载均衡,这依赖于具有强大搜索能力的智能优化算法.目前,已经有诸多的智能优化算法应用于云计算资源调度中.针对云计算服务集群资源调度和负载平衡的优化问题,刘万军[2]等提出了一种适用于云计算资源调度的粒子群改进算法.针对目前静态的网络资源调度算法不能满足动态的云计算资源调度要求的问题,周文俊[3]等提出了一种基于预测及蚁群算法的云计算资源调度策略.为了提高云计算资源的利用率,以保持负载平衡,孟令玺[4]等提出一种适用于云计算资源调度的文化粒子群算法.为了提高云计算资源的调度效率,袁浩[5]等提出了一种适合于云计算资源调度的社会力群智能优化算法.针对传统资源调度算法中存在资源利用率低等缺陷,卓涛[6]等提出一种基于改进人工蜂群算法的云计算资源调度模型(Improved Artificial Bee Colony,IABC).尽管上述的改进算法在一定程度上能够提升云计算资源调度的效率和精度,但仍有一些不足之处.

云计算调度问题极难求得令人满意的解.这一方面是因为云计算资源问题具有大规模、非线性、逻辑复杂的特点,另一方面则是由于现有的智能优化算法及其改进策略都存在着对模型参数敏感、迭代后期容易陷入局部收敛等缺陷.为有效弥合智能优化算法的缺陷以改善其优化性能,本文提出了一种云计算调度粒子群改进算法.基于云资源调度优化模型,本文将混沌随机数扰动引入现有的惯性权重线性递减(LDW)粒子群算法中,且结合了蚁群算法的寻优策略.基于2 种测试函数和1 个云计算资源调度实际算例对3 种不一样的优化算法进行比对试验,其对比试验结果表明,本文提出的粒子群改进算法的算法性能更佳.

1 云计算资源调度问题的优化模型

云计算资源调度问题的核心是节约其执行任务的时间.因此,云计算资源调度问题中最重要的优化目标即是其最大任务的执行时间,记为Tmax.此外,云计算资源调度的重要优化目标是负载不平衡程度,记为Bdegree.具体的以花费时间和负载平衡作为优化目标的优化模型为[7]:

式(2)中,M={1,2,3,···,m}为 任务集合,含m个不同的任务；N={1,2,3,···,n}为 节点集合,含n个不同的节点；tij为第i个任务在第j个计算节点上的估算执行时间；eij是决策变量,为第j个计算节点上执行第i个任务,若是,则eij=1,否则,eij=0.

最大任务的执行时间Tmax采用下述公式计算得到:

负载不平衡程度Bdegree采用下述公式计算得到:

式(3) 中,enum={e1num,e2num,···,ennum,} 为n个不同节点的执行次数的集合,E(X) 为 集合X的方差.

上述优化模型求得最优需使得任务完成时间最短,也即:

式中,cost为最短的任务完成时间.

由上述云计算资源调度问题的优化模型可知,采用传统的梯度下降算法等常规算法是不易求得满意的优化解的,因此,一般会采用粒子群算法等智能优化算法进行求解.

2 改进的粒子群算法

2.1 粒子群算法

美国心理学家Kennedy 和电气工程师Eberhart 于1995年共同提出了粒子群算法(PSO)[8].假设群体规模为N,目标空间维度为D,第i个粒子的坐标位置向为=(xi1,xi2,···,xiD)T、 速度向量为=(vi1,vi2,···,viD)T,个体极值和全局极值分别为=(pi1,pi2,···,piD)T、=(pg1,pg2,···,pgD)T.具体的粒子群算法的更新迭代计算公式如式(5)所述.

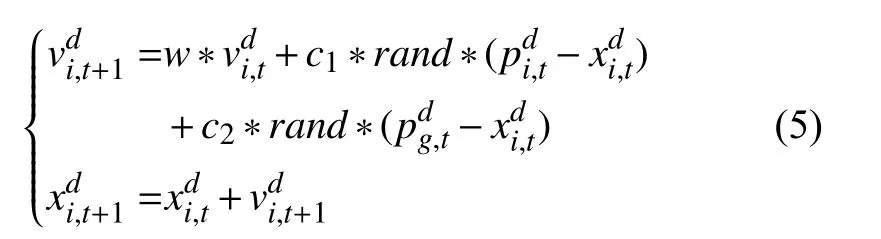
式中,i=1,2,···,N为粒子序号,t为 粒子维度,d为迭代次数,w为权重因子,c1,c2为加速随机数,一般来说,c1,c2∈[0,2],rand∈[0,1],也为随机数.

2.2 惯性权重线性递减的粒子群算法

为改善粒子群算法极易陷入局部收敛的缺陷,众多学者考虑了一种惯性权重系数 ω 线性递减的改进策略.具体的惯性权重线性递减的粒子群算法更新迭代计算公式如式(6)所述.

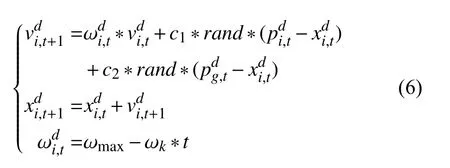
式中,ωmax为惯性权重最大值,ωk为惯性权重递减斜率.

惯性权重ω 是一个粒子群算法的重要参数.其能够使粒子保持运动惯性,从而有能力对新区域进行搜索.惯性权重的增大对全局搜索有帮助,有助于加快其收敛速度,但不利于寻到精确解；惯性权重的减小对局部搜索有帮助,从而可以获得到更精确的解,但代价却是降低了算法的收敛速度和增加了算法局部收敛的概率.因此,惯性权重的取值需要同时兼顾收敛速度和寻优精度.由上述分析可知,对于粒子群算法而言,其迭代前期,收敛速度的重要性较大；随着迭代次数的增加,寻优精度的重要性越来越大.

惯性权重线性递减(Linear Decreasing inertia Weight,LDW)的具体策略如下所述:在LDW 粒子群算法的整个过程中,以进化代数为标准,惯性权重以ωk的递减斜率线性递减.其惯性权重 ω和进化代数t的关系曲线如图1所述.

图1 惯性权重线性递减下的惯性权重ω 和进化代数t的关系曲线

2.3 增加混沌随机数扰动的惯性权重线性递减粒子群算法

惯性权重线性递减(LDW)粒子群算法较基本粒子群算法而言,具有更好的寻优性能.然而,由于粒子群算法实际搜索过程具有非线性的特点,于是惯性权重 ω线性递减不能体现实际搜索过程的非线性的特点,因而导致得不到足够理想的优化效果[9].因此,粒子群算法实际计算过程中,若算法通过长时间的计算都无法获得更理想的全局极值,即迅速加入合理范围内的混沌随机数扰动,以使得惯性权重 ω突然增大,从而起到抑制粒子群算法局部收敛的作用[10].其增加混沌随机数扰动的惯性权重线性递减的粒子群算法更新迭代计算公式如式(7)所述.

式中,At为惯性权重的混沌扰动随机数,在一定的扰动概率下,At∈{0,0.1},其余,At=0.混沌现象是非线性系统中一种普遍的现象,它的变化过程看似混乱,实际上其内在具有规律性,能够在一定范围之内,按照自身规律不重复地遍历所有状态.具体的惯性权重的混沌扰动随机数At的随机公式如下所示:

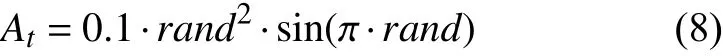
其增加混沌随机数扰动的惯性权重 ω和进化代数t的关系曲线如图1所述.

图2 增加混沌随机数扰动的惯性权重线性递减下的惯性权重ω 和进化代数t 的关系曲线

2.4 蚁群算法

1992年,意大利学者Dorigo 提出了蚁群算法[11].在蚁群算法中,每只蚂蚁均在进行路径搜索后独立的产生一个可行解,并产生信息素.假设当前共有m个节点等待蚂蚁访问及选择,在t时 刻,第k只蚂蚁正处于节点i处,即将选择下一节点j进行移动,其移动规则如下:

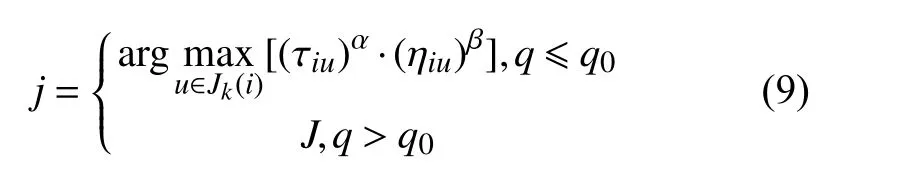
每只蚂蚁在构建可行解的同时分泌信息素,局部信息素更新方式如下式所示:

当一次循环中的所有蚂蚁均构建了可行解后,对该次循环产生的最优解与已知的最优解进行比较,判断是否产生了新的当前的最优解,若产生,则对该解上的弧信息素进行更新,如下式所示:

式(8)-(10)中,蚁群算法主要变量如下:τij为 弧(i,j)上的蚂蚁信息素密度,初始值为 τ0；dij为弧(i,j)上的欧式长度；ηij为弧(i,j)上 的启发函数值,通常ηij=1/dij；α为蚂蚁信息素密度的相对重要性,α ≥0；β为启发函数的相对重要性,β≥0；ρ为蚂蚁信息素的衰减参数,0＜ρ＜1；Lbest为当前最优解的路径长度；Vbest为当前最优解.

2.5 混合优化算法改进策略

粒子群算法和蚁群算法的寻优模式相对单一,总是全部个体向最优个体进行学习,其最优解对种群的进化方向的影响是很大的.为了克服采用单一的有相对固定寻优指引方向的寻优模式导致的算法容易陷入局部最优的缺点,本文提出了一种同时混入蚁群优化策略的改进LDW 粒子群优化策略的混合优化算法,记为Improved PSO.目的在于在保持原有粒子群算法和蚁群算法搜索性能的同时,防止算法因为寻优模式单一而导致的陷入局部收敛的缺点.具体的计算步骤如下所述:

Step1.初始化混合优化算法的各项参数:种群规模m+N、粒子群规模(粒子数量)N、迭代次数d、最大惯性权重ωmax、惯性权重系数的递减斜率 ωk、学习因子c1,c2、蚁群规模(蚂蚁数量)m、蚂蚁信息素密度的相对重要性 α、启发函数的相对重要性 β、蚂蚁信息素的衰减参数 ρ等,其中的粒子群规模与蚁群规模相同m=N；

Step2.随机生成m+N种不同的解,也即生成初始种群,初始种群包含初始粒子群和初始蚁群；

Step3.计算N种解的适应度函数值,并基于此对当前粒子群进行排序,以得到个体极值和全局极值；

Step4.采用增加混沌随机数扰动的惯性权重的线性递减(LDW)粒子群算法的更新规则对所有粒子进行更新；

Step5.将这m只 “蚂蚁”置于起始结点0 上,采用蚁群算法的信息素更新规则对所有蚂蚁进行更新；

Step6.粒子群和蚁群交换一定数目k的个体,其交换数目要小于粒子群规模和蚁群规模k＜min(m,N)；

Step7.查看是否达到最大迭代次数,如果是则转步骤Step5,否则转步骤Step2；

Step8.输出计算得到的最优解的适应度函数值.

本文中,粒子群算法和蚁群算法的主要参数如下:粒子群规模N为30、迭代次数d为50、最大惯性权重ωmax为0.85、惯性权重系数的递减斜率 ωk为0.001、学习因子c1,c2均为0.5、蚂蚁信息素密度的相对重要性 α为1、启发函数的相对重要性 β为0.9、蚂蚁信息素的衰减参数ρ 为0.2.

3 仿真实验

基于2 种不同的测试函数,采用粒子群改进算法(IPSO)、增加混沌随机数扰动的惯性权重线性递减(LDW) 的粒子群算法[12](linear decreasing inertia weight PSO with chaotic constant disturbance,CLDWPSO)和普通的惯性权重线性递减粒子群算法[13](Linear Decreasing inertia Weight PSO,LDWPSO)求极小值.具体的仿真结果如下所述.

(1) De jong 函数,最优解为0.0.其De jong 函数的解析式为F(x1,x2)=100∗(x1-x2)2+(1-x1)2.

具体的De jong 函数的仿真测试结果如图3和表1所 述.

图3 采用De jong 函数的仿真测试收敛曲线

由图3和表1可知,相比于其它算法,粒子群改进算法(IPSO) 最优,寻优得到的最优解为:(x1,x2)=(0.9928,0.9984)；最优解函数值F(x1,x2)=0.0032.与此同时,粒子群改进算法(IPSO) 的收敛时间最短,为2 0.21 秒.

表1 采用De jong 函数的仿真测试结果

(2) Schaffer 函数,最优解0.0.其Schaffer 函数的解析式为

具体的Schaffer 函数的仿真测试结果如图4和表2所述.

表2 采用Schaffer 函数的仿真测试结果

由图4和表2可知,粒子群改进算法(IPSO)同样最优,寻优得到的最优解为:(x1,x2)=(2.8×10-4,2.2×10-4) ；最优解函数值F(x1,x2)=3.62×10-4.与此同时,粒子群改进算法(IPSO) 的收敛时间最短,为43.86 秒.

4 实际算例测试

为了验证算法的改进效果,本文采用粒子群改进算法(IPSO)、增加混沌随机数扰动的惯性权重线性递减的粒子群算法(CLDWPSO)和普通的惯性权重线性递减粒子群算法(LDWPSO)求解了一个云资源调度实际算例的最短任务完成时间及其不平衡程度.实际算例有10 个计算节点和100 个任务.具体的云资源调度问题的估算执行时间表如表3所述[14].

表3 云资源调度问题的估算执行时间表

具体的云资源调度问题的实测收敛曲线如图5和图6所述.

图5 云资源调度问题任务完成时间的实测收敛曲线

图6 云资源调度问题负载不平衡程度的实测收敛曲线

由图5和图6可知,相比于其它算法,粒子群改进算法(IPSO) 最优,求解得到的任务执行节点序列为e=[7 4 1 7 5 7 10 ···9],估算的任务完成时间为194.4568.与此同时,粒子群改进算法(IPSO)寻到的调度方案的负载不平衡程度最小,为0.4444,其调度方案的计算节点的执行次数的集合为enum=[10 10 9 ···9].

5 结论

本文基于云资源调度问题的优化模型,提出了一种粒子群改进算法(IPSO).首先,基于惯性权重线性递减粒子群算法,引入适当的混沌随机数扰动；其次,将蚁群算法寻优策略引入粒子群算法中以改善其全局优化性能.本文采用了2 种测试函数(De jong、Schaffer)和1 个云计算资源调度实际算例来验证优化算法的性能.其验证结果表明,相比于其他两种优化算法,本文提出的改进算法(IPSO)更佳.