基于L1图的联合稀疏鲁棒判别回归*
牛 强, 陈秀宏
(江南大学 数字媒体学院,江苏 无锡 214122)
0 引 言
近年来,人脸识别在计算机视觉等领域成为学者们的研究热点[1~3],最小二乘回归已在计算机视觉领域得到了广泛运用。回归算法以及延伸算法主要分为稀疏回归、子空间回归和鲁棒回归等三类。稀疏回归[4]方法是在最小二乘回归中加入不同的正则化项,因在回归模型中使用了标签指示矩阵而最多只能得到c个投影(c为样本类的个数)。子空间回归方法是将许多线性降维算法表示为最小二乘回归模型,例如,文献[5]给出了许多成分分析方法的最小二乘统一框架。子空间回归的算法因在回归模型中未使用标签指示矩阵,从而可获得更多的投影方向(数量大于c个)。然而,以上两种回归方法均使用L2范数或Frobenius范数作为距离度量,因此对含有异常值的数据较敏感。鲁棒回归是在回归模型中采用L2,1范数表示损失函数,文献[6]利用L2,1范数表示损失函数而提出了鲁棒判别回归(robust discriminant regression,RDR)方法,并取得了较好的性能。由于L2,1范数正则化项能够联合地获得稀疏性,Gu Q等人[7]提出了基于局部保留投影(locality preserving projection,LPP)的联合特征选择和子空间学习算法(joint feature selection and subspace learning,FSSL)。由于L2,1范数在特征选择和特征提取时能获得联合稀疏的特性,因此,被广泛应用于稀疏回归和子空间学习的研究中[8]。以上回归方法忽略了数据的局部几何特性,通过图矩阵来表示数据的局部几何结构信息,从而可得到有鉴别能力的低维特征。传统的构造图方法通常采用k近邻法和ε近邻法,参数k或ε的选择直接影响到算法的性能,另外权值对数据噪声也非常敏感。Cheng B等人[9]提出了L1图构造方法,具有抗噪声能力强、良好的稀疏性以及数据自适应的邻域关系等特性,通过这种方式,图的邻接关系和权值能够同时自动获得。
为了充分利用子空间回归以及鲁棒回归方法的优点(即在模型中不使用标签指示矩阵同时使用L2,1模表示损失函数),这样可获得更多的投影方向,使得算法对含有异常值的数据具有鲁棒性,同时为了能揭示数据的局部几何结构,本文提出一种基于L1图的联合稀疏鲁棒判别回归算法(joint sparse robust discriminant regression based on L1 graph,L1-JSRDR)。首先利用稀疏表示构造L1图,然后将图权值矩阵融入到基于L2,1模的损失函数中,最后通过交替迭代方法求出模型的最优解。该回归模型增强了学习的鲁棒性,并在多个人脸库上进行实验,验证了新算法的有效性。
1 相关工作
设给定一组样本X=[x1,x2,…,xN|∈RN×m,其中行向量xi∈R1×m为样本,m为样本的维数,N为样本的个数。
1.1 基于稀疏表示的L1图
在常用k近邻法构造图方法中,其图权值矩阵定义为
式中xi∈Nk(xj)为样本xi位于xj的k邻域Nk(xj)内。但该方法对数据噪声非常敏感且严重依赖于参数k的选择,很难有效地反映数据分布的复杂性。
基于稀疏表示的L1图构造原理是:任一样本均可以由其他样本线性地重构,通过求解一个L1范数优化问题得到样本的稀疏重构系数;将重构系数作为两个样本之间的权值,从而得到L1图。该方法能自适应地调整样本之间的关系,使得表示样本间局部关系的稀疏图能包含更有用的结构信息和样本之间的相似度。构造L1图的过程如下:
1)输入训练样本集X,并进行归一化处理。
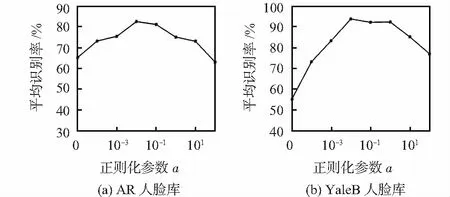
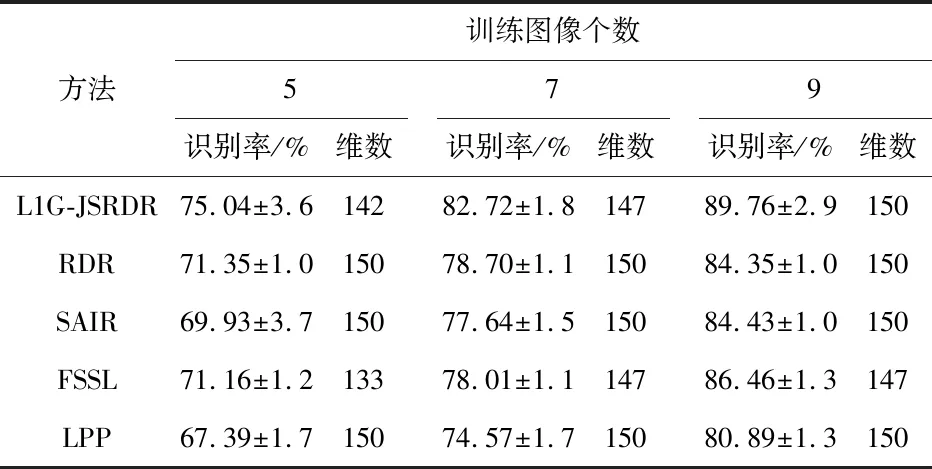
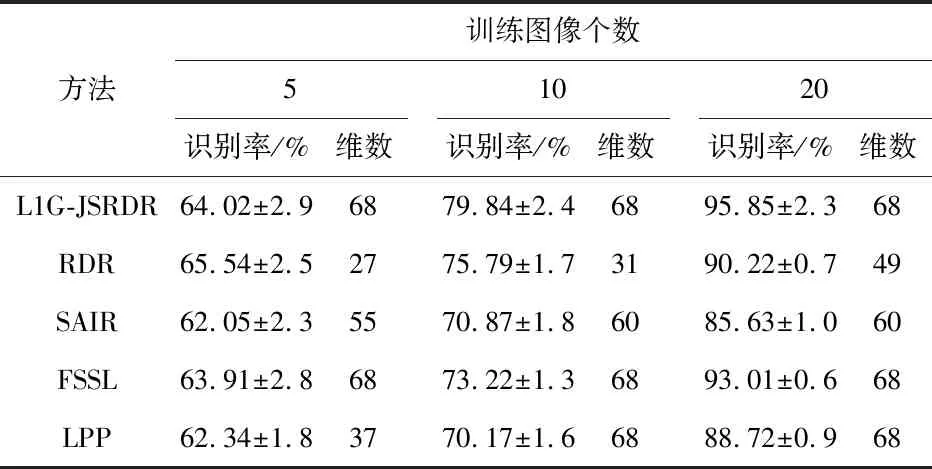
2)求解重构系数:对每一个样本xi(1 式中Bi=[x1,…xi-1,xi+1,…,xN,I]∈Rm×(m+N-1)为一个超完备的字典,重构系数列向量ai∈Rm+N-1为样本xi与其余样本之间的相似关系,I为单位阵。 上述所构造L1图的方法避免了传统构造图方法中对参数的人工干预,同时该图对噪声具有鲁棒性。求解L1范数稀疏问题有很多优化工具包,本文采用SPAMS(http://spams-devel.gforge.inria.fr/index.html)优化工具包来进行求解。 式中 loss(·)为损失函数,yi为样本xi的标签,R(f)为正则化项,α为正则化参数。然而,该回归模型只能获得c个投影,影响了回归的性能。为此,考虑以下优化回归模型 式中g(·)为定义在数据集上的函数,为了进一步提高特征提取的鲁棒性,将数据的局部几何信息融入到回归模型中,其中wi,j为图的边权值,表示数据的局部流形结构。该模型放弃了标签信息从而可获得更多的投影,有效地提高了回归方法的性能。 如将L1图的权融入损失函数之中并对投影矩阵加上L2,1模约束,那么应能获得行稀疏的投影矩阵,同时还能保持数据的局部几何结构,从而可提取更具有判别能力的特征,进一步提高算法的性能。考虑回归模型(4)的以下形式,称之为基于L1图的联合稀疏鲁棒判别回归模型 式中 矩阵Q∈Rm×d为投影矩阵,矩阵P∈Rd×m表示重构矩阵,α为正则化参数。目标函数中的第一项表示在L1图下样本xi与样本xj经过投影和重构后所得xjQP之间的误差,这样如果样本xi和xj彼此接近,则xi与xj在矩阵QP的映射下的xjQP也应该彼此接近,从而保持了数据的相似性或几何结构;模型的第二项使得投影矩阵Q∈Rm×d的行是稀疏的,这样就能提取更多有用的特征。式(5)的目标函数可表示为 式中 矩阵U中的元素和对角阵G的对角元素分别为 tr(XTDX-2PTQTXTFX+PTQTXTDXQP)+αtr(QTGQ) (8) 从而,优化模型(5)转化为 αtr(QTGQ),s.t.QTQ=I (9) 采用交替迭代优化方法求解上述模型,即先固定Q求矩阵P,再固定P求Q。因为每次迭代中由已知的矩阵Q和P计算矩阵D,所以tr(XTDX)在交替迭代计算时为一个常数,模型(9)可转变为 s.t.QTQ=I (10) 固定Q求矩阵P,式(10)中目标函数关于矩阵P求偏导并令结果为0可得 P=(QTXTDXQ)-1QTXTFX (11) 其次,固定P求Q,对于求最优矩阵Q通过对式(10)关于矩阵Q构造拉格朗日函数,可得 L(Q,λ)=tr(-2PTQTXTFX+PTQTXTDXQP)+ αtr(QTFQ)-λ(QTQ-I) (12) 式中λ为拉格朗日乘子,通过对式(12)关于矩阵Q求偏导并令结果为0可得 XTDXQPPT+αGQ-λQ=XTFXPT (13) 可将式(13)表示为分块矩阵形式可得 (14) Q=E(HHT)-1H (15) 由于矩阵W的秩rank(W)=c(c表示样本的类别数),矩阵U通常为满秩矩阵,rank(XTFXPT)=rank(F)=rank(U⊙W),而rank(U⊙W)≥rank(W)=c,同时rank(U⊙W)≤rank(U)=N,可知本文模型可以获得的投影至少有c个,进一步表明了算法具有较好的特征提取能力。 由以上讨论,给出本文的L1G-JSRDR算法流程如下: 1)输入样本集X,维数d,正则化参数α,参数λ; 2)初始化G=I,U=I,随机初始化矩阵Q∈Rm×d,P∈Rd×m; 3)通过稀疏表示构造L1图权重矩阵W; 4)Repeat a.计算矩阵XTDX和XTFXPT b.通过式(15)求解矩阵Q c.通过式(11)求解矩阵P d.更新矩阵U,G,F,D Until目标函数收敛 End 5)得到投影矩阵Q 本文在AR和YaleB含有异常值的人脸库进行了仿真实验,对LIG-JSRDR、RDR[6]、FSSL[7]、LPP[7]和SAIR[8]进行比较。RDR、FSSL和LPP算法利用式(1)计算图权值矩阵,因本文算法获得投影至少有c个,实验中维数d的值设置为c+20;本文算法的微调参数λ的取值范围的[0.001,0.01,0.1,1,5,10]。所有实验均独立随机进行了20次,采用最近欧氏距离最近分类器进行分类。 AR人脸库使用了其中的120人的图像,每人26张,共3 120张图像。实验在YaleB人脸库上随机加入5像素×5像素和10像素×10像素大小的黑色方块遮挡,用于验证本文算法对遮挡图像的鲁棒性。 为了研究正则化参数α对L1G-JSRDR算法识别率的影响,其中在AR人脸库和5×5的黑色遮挡的YaleB人脸库上每人选择7幅和20幅图像作为训练,其余图像作为测试。平均识别率和正则化参数α的关系如图1所示。 图1 平均识别率与正则化参数的关系 由上图可知,算法在α=0时由于未加入L2,1范数的惩罚项,识别效果较差,随着α值的不断增大,算法达到最佳效果,之后识别效果又开始降低,这表明了本文算法的正则化项在特征提取时可以提高判别性能和模型的泛化能力。当α的取值在一个范围内算法仍保持较高识别率,为了更好的比较算法的性能,以下实验在AR人脸库的实验中a的取值范围为[0.01,0.1];在YaleB人脸库的实验,α的取值范围为[0.01,0.1,1]。 3.3.1 特征维数对实验的影响 在AR人脸库和10×10遮挡的YaleB人脸库上,每人随机选取7幅和20幅像进行训练,其余的图像作为测试样本。图3为不同人脸库上提取的特征向量维数与平均识别率的关系。 图2 平均识别率与特征维数的关系 由图2可知,本文算法在2个人脸库上在取最高维时识别性能最优。FSSL算法在AR和YaleB人脸库上的识别率随着特征维数的增加达到峰值后又下降,其余算法的识别率均随着特征维数的增加而增加。由YaleB人脸库结果可知,L1G-JSRDR算法在较低维时并不能达到很好的识别性能,当随着维数增大时,算法的识别性能开始增加,可能是由于在图像上增加噪声和遮挡等异常数据使得本文算法在较低维时的识别性能受到影响。由AR人脸库上可知,L1G-JSRDR算法在绝大多数维度下,算法的识别率都高于其他算法。在2个人脸库上能够取得较好的识别效果,这是因为本文算法采用了基于L2,1范数的表示损失函数,使得算法对含有异常值的图像具有鲁棒性,同时能够获得更多的投影方向,同时加入了L2,1范数的惩罚项后可以使得投影矩阵稀疏,能够防止过拟合问题,算法能自动的选取特征,从而提高了识别性能。 3.3.2 样本数对实验的影响 在AR人脸库上,每人随机选择5,7,9幅图像进行训练,在含有5×5遮挡的YaleB人脸库上,每人随机选取5,10,20幅像进行训练,其余的图像作为测试样本。表1,表2列出了算法取得的最佳平均识别率、标准差及其对应的特征维数。 表1 AR人脸库上各算法的平均识别率、标准差和维数 表2 YaleB人脸库上各算法的平均识别率、标准差和维数 如表1、表2所示,L1G-JSRDR算法的识别率最高且整体上相对稳定。因为L1图具有较强的抗噪声能力和数据自适应的邻域关系的特性,实验结果表明L1G-JSRDR算法比传统手工设置近邻参数的构图算法(如RDR,FSSL和LPP)的识别率都要高。L1G-JSRDR的识别率比RDR算法高,这是因为算法利用L1图构造权值矩阵,更好地保留了样本的局部几何结构,且加入了L2,1范数的正则化项,使得投影矩阵行稀疏,自动抛弃了一些对分类没用的特征,有利于特征的选取,提升了模型的泛化能力。与RDR和L1G-JSRDR等基于L2,1范数的回归方法相比,SAIR算法的识别率并不高,原因是SAIR算法在模型中没有利用图矩阵保持数据的局部几何结构,同时回归步骤使用了标签矩阵,使得算法只能获得c个投影,一定程度上限制了识别性能。 在含有异常值的人脸库上进行实验表明:本文算法具有较好的鲁棒性,取得了较优异的识别性能。相对于传统近邻构图,文中提出的基于稀疏构图方法复杂度相对较高,且计算成本相对较大,如何降低复杂度值得进一步研究。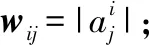
1.2 回归模型
2 基于L1图的联合稀疏鲁棒判别回归



3 实验结果与分析
3.1 实验环境
3.2 正则化参数α对实验的影响
3.3 识别性能分析

4 结 论

