灰色凸关联的进一步拓广

金梦迪，张辉，刘基伟

(中国传媒大学 数据科学与智能媒体学院，北京 100024)

1 引言

灰色关联分析是灰色系统理论的重要内容之一，是灰色关联评估与决策、灰关联控制的基础，由于它对样本量要求低、分布规律无需典型、计算量小且定量定性可以结合的特点，近年来在理论与应用方面的研究得到了广泛重视。然而，自从1982年以来灰色系统理论创立以来，关于灰色关联度模型的研究都是以各个时刻点灰色关联系数的简单算术平均数作为灰色关联度，这样就会造成信息的损失和局部点关联测度值控制整个灰色关联度的倾向，针对这个问题，为确保新信息优先性，因此本文又提出一中基于时间加权的灰色凸关联度。

2 灰色凸关联度

对于定义在集合S上的函数，任意的x1，x2∈S有

则称函数f是集合S上的凸函数，所以对离散的点集，有以下的定义：

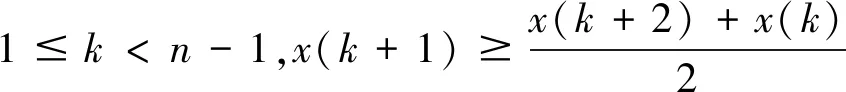
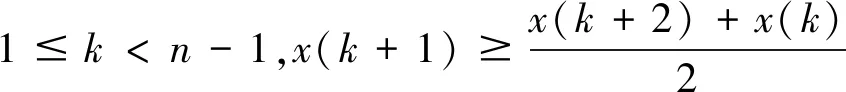
定义2对正离散系统行为序列称

为X在点t=k+1处的相对凸度。

显然，当X为正凸序列时，相对凸出为正数，数值越大，相对凸程度就越大；当X为正凹序列式，相对凸度为负数，数值越大，相对凹的程度越小。

命题1对正离散系统行为序列X=(x(1)，x(2)，…，x(n))，依次作数乘变换、平移变换得：

X1=(x1(1)，x1(2)，…，x1(n))，

x1(i)=cx(i)，i=1，2，…，n，c>0，

X2=(x2(1)，x2(2)，…，x2(n))，

则对任意i∈{2，3，…，n-1}，X与X1在i处的相对凸度相同；X在X2处i的相对凸度一般不同。

定义3对正离散系统行为序列

X0=(x0(1)，x0(2)，…，x0(n))，X1=(x1(1)，x1(2)，…，x1(n))，…，Xm=(xm(1)，xm(2)，…，xm(n))，

称

为X0，X1的灰色凸关联系数，其中di(k)是序列Xi在t=k处的相对凸度，i=0，1，2，…m，k=2，3，…n-1。称

为X0，Xi的灰色凸关联度。若对相关因素行为序列Xi，Xj有γ0i>γ0j，则称X0，Xi的关联优于因素的关联X0，Xj记为X0≻Xi，称为≻由灰色凸关联度导出的灰色凸关联序。

3 加权灰色凸关联度

定义4对正离散系统行为序列

X0=(x0(1)，x0(2)，…，x0(n))，X1=(x1(1)，x1(2)，…，x1(n))，…，Xm=(xm(1)，xm(2)，…，xm(n))，

称

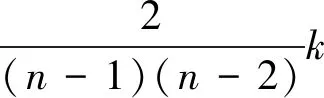
定理1灰色加权凸关联度具有以下性质：

(1)规范性，0<γ0i≤1；

(2)对称性，即γ0i=γi0；

(3)新信息优先性

(4)接近性，即相对凹凸程度越接近，关联度越大；

(5)可比性，唯一性；

(6)数乘变换一致性；

(7)数乘变换保序性；

(8)灰色关联序干扰独立性。

定理2加权灰色凸关联度满足新信息优先性

对正离散系统行为序列X0=(x0(1)，x0(2)，…，x0(n))，Xi=(xi(1)，xi(2)，…，xi(n))之间的灰色凸关联系数γ0i(k)，如果最后一个数据发生扰动即γ0i(n)*=γ0i(n)+ε则X0，Xi的灰色关联度

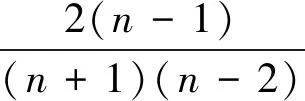
记灰色关联度扰动值为δγ0i则

类似的，当扰动发生在其他位置时，即γ0i(k)=γ0i(k)+ε，我们可以获得扰动

当n固定时，随着k的增大，扰动值δγ0i递增，即越新的数据发生扰动，灰色关联度的扰动范围越大，满足新信息优先性。

算例分析

已知X0为主行为序列，X1，X2，X3为比较序列，具体数据如下

X0=(1.0，2.0，2.5，2.5，3.0，5.0，8.0)

X1=(1.0，1.8，2.3，2.4，2.8，4.8，1.2)

X2=(3.0，1.8，2.3，2.2，3.0，4.1，6.0)

X3=(2.6，2.1，2.5，2.1，3.0，4.1，5.7)

得到的灰色关联系数如下

综上所述，三维步态分析结合三维测力台及无线表面肌电图在评价人体步行过程中下肢关节的运动学、动力学、地面反作用力，及表面肌电信号时具有良好的重复性，这将有助于对不同患者步行功能进行精确的量化评估，也可用于检测患者在步行过程中下肢各个关节在矢状面、冠状面、水平面上所承受的应力，及相应肌肉的收缩时序等。使用三维步态分析技术除了可用于临床诊断外也可为疗效评估以及相关治疗的机理研究提供更精确可靠的数据和理论基础，因此值得进一步推广。

γ01(k)=(0.960，0.987，0.963，0.965，0.594)

γ02(k)=(0.626，0.931，0.816，0.810，0.997)

γ03(k)=(0.746，0.943，0.826，0.821，0.962)

按原灰色凸关联度公式计算得

γ(X0，X1)=0.894，γ(X0，X2)=0.836，γ(X0，X3)=0.860，

因此灰色关联序为

γ(X0，X1)≻γ(X0，X2)=γ(X0，X3)

然而按照灰色加权凸关联度计算得

因此灰色关联序为

γ(X0，X3)≻γ(X0，X2)=γ(X0，X1)

由此可见，灰色加权凸关联度充分体现新信息的作用，解决了旧信息扰动控制整个灰色关联序的问题。

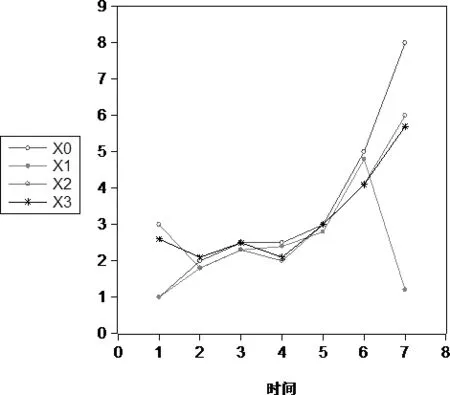
图1

图1可见，序列x2，x3更接近x1的发展态势，然而按原先的灰色凸关联模型却得到相反的结果。

4 实例研究

研究2010-2016年中国城镇居民消费价格指数相关指标的主次关系，数据来源：《中国统计年鉴》，数据序列为：

城镇居民消费价格指数X0=(676.5，662.6，652.8，639.4，623.2，606.8，576.3)

城镇居民人均可支配收入X1=(33616，31195，28844，26467，24564，21809，19109)

城镇居民人均消费支出X2=(23079，21392，19968，18488，16674，15160，13471)

城镇单位平均工资X3=(67569，62029，56360，51483，46769，41799，36539)

由未加权模型计算得到灰色关联度如下

γ01=0.99102，γ02=0.99478，γ03=0.99435

因此灰色关联序为：

γ02≻γ03≻γ01

而由本文加权模型计算得到灰色关联度如下

γ01=0.98921，γ02=0.99412，γ03=0.99431

因此灰色关联序为：

γ03≻γ03≻γ01

两种方法都表明城镇单位平均工资对城镇居民消费价格指数的影响要高于城镇居民人均可支配收入；与未加权模型相比，近年来，城镇单位平均工资对城镇居民消费价格指数的影响越来越大。

5 结论

本文灰色加权凸关联度模型适用于注重时间因素的关联分析问题，且序列的意义、量纲不影响关联度的大小。结果表明，该方法能够反映不同时间点的重要性，优化了新信息作用，对灰色关联系数的波动同时得到了有效控制，解决了旧信息扰动控制整个灰色关联序的问题。