包含乘性噪声自适应修正的非合作目标相对导航算法

朱云峰，孙永荣，赵伟，黄斌，吴玲

南京航空航天大学 自动化学院，南京 210016

近年来，随着无人机应用领域的不断拓展，其对态势感知的要求也越来越高，尤其是对于未知环境的探索能力，是急需攻克的重点问题。相对导航作为其中的核心技术之一[1]，在未来的智能物流、集群作战[2]、搜索救援和编队飞行[3]等多种场合都至关重要。因此，实时、高精度、高可靠性的相对状态估计算法逐渐成为研究的热点内容[4]。

非合作目标的相对导航主要是指在没有通信条件，或者目标上没有配置主动传感器的情况下的相对定位问题[5]。合适的传感器选择是非常关键的。目前，对于中远距离的相对导航，根据传感器的测量原理可以分为多种，包括视觉传感器、雷达、IRST(Infrared Search and Track)和ESM(Electronic Support Measures)等以波达角度(Angle of Arrival，AOA)或距离为量测的传感器[6]，或者以波达时间(Time of Arrival，TOA)[7]、波达频率(Frequency of Arrival，FOA)[8]、波达时间差(Time Difference of Arrival，TDOA)[9]等为量测值的无线电设备。本文以视线仰角、视线方位角和无人机与目标之间的直线距离作为传感器输出来估计相对状态。

对于非线性系统的状态估计算法，目前扩展卡尔曼滤波(EKF)算法是使用最广的，但由于其经过泰勒展开后取一阶线性近似[10-11]，忽略了高阶项的非线性特性，在一些强非线性的情况下导致滤波精度严重下降，并且收敛速度缓慢[12]。为了进一步改善算法的性能，迭代扩展卡尔曼滤波(IEKF)算法发展起来，并开始得到应用。但该算法通过多次使用量测值实现，当迭代初值或者协方差误差较大时，容易找不到极值点，明显降低了滤波器的精度[13]。同时，对于非合作目标相对导航系统而言，距离的测量往往与信号特性相关联，测量中的抖动振动造成安装矩阵与基准之间的偏转以及信号能量的衰减都会引入乘性误差[14-15]。但目前的相对导航滤波算法基本都将距离量测噪声设定为加性噪声，没有对因相对距离的增加而引入的乘性量测噪声进行修正，如果只是简单地以传感器的标称值或实验室测定值设置滤波中的噪声阵，必将导致滤波精度的污染[16]，造成仿真实验和实际的不一致性。

鉴于上述的问题，本文通过分析IEKF算法中的迭代过程，利用LM(Levenberg-Marguardt)优化的思想进行改进，提出了一种LM-IEKF(Levenberg-Marquardt Iterative Extended Kalman Filter)算法，考虑到乘性噪声情况下的精度下降问题，又进一步提出了包含有量测噪声自适应修正的Modified LM-IEKF算法。最后，通过对比分析验证了本文算法的有效性。

1 非合作目标相对导航系统模型

非合作目标的相对导航是通过无人机对目标进行测角测距来实现的，无人机与目标之间的位置关系如图1所示，xyz坐标系为地心空间直角坐标系，ρ为无人机测得的目标距离,β和α分别为无人机对目标探测得到的视线仰角和视线方位角(本文中规定视线方位角为与x轴正方向的夹角)。

图1 相对导航原理示意图Fig.1 Schematic diagram of relative navigation

根据定位原理，可以得到空间几何模型。将无人机的绝对位置坐标记为Xu=[xu,yu,zu]T，目标的绝对位置坐标记为Xt=[xt,yt,zt]T。相对导航的目的就是利用无人机上配置的传感器测量得到距离和角度信息[ρ,α,β]，计算出目标与无人机间的相对位置ΔX=Xt-Xu=[Δx,Δy,Δz]T。由图2可以得到无人机与目标之间的空间几何关系为

(1)

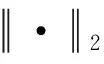
定义状态变量为x= [ΔX, ΔX′, ΔX″]T，其中ΔX′和ΔX″分别为无人机与目标之间的相对速度和相对加速度。由式(1)可以建立相对导航系统的量测方程为

(2)

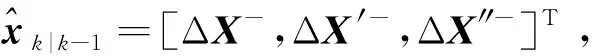
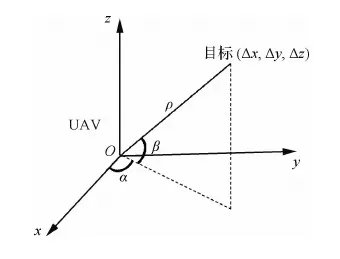
图2 相对导航几何空间模型示意图Fig.2 Relative navigation geometric space model

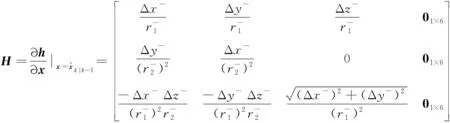
(3)

式中：

选择匀加速(CA)模型作为相对运动模型，离散化状态方程可表示为

xk=Φk|k-1xk-1+Γk-1wk-1

(4)

式中：状态转移矩阵Φk|k-1和噪声输入矩阵Γk-1分别为

(5)

2 基于Levenberg-Marquardt优化的迭代卡尔曼滤波算法

基于上述的相对导航数学模型，本节分析了IEKF算法原理，并引入Levenberg-Marquardt优化的思想对其进行改进，进而提出了一种提高滤波稳定性的LM-IEKF算法。

2.1 现有的IEKF算法

传统的EKF算法可以一定程度地解决非线性滤波问题，但由于其在使用泰勒阶数展开时，舍去了高阶项，所以滤波过程中产生了截断误差。尤其当系统模型存在较大的误差时，经非线性函数放大之后可能会导致滤波结果偏差很明显并出现滤波不稳定的情况，在实际情况中甚至会出现滤波发散。

IEKF算法是EKF的一种改进，其以状态估计值为依据，针对观测矩阵的计算，通过设置迭代次数进行多次更新，反复使用观测数据，可以有效地改善状态估计的精度[10,12,13]。

算法在k时刻的第次迭代流程如下：

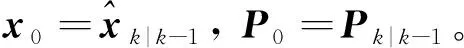
2) 求雅克比矩阵Hk,i：

(6)

3) 求增益阵Kk,i：

Kk,i=Pk|k-1(Hk,i)T(Hk,iPk|k-1(Hk,i)T+Rk)-1

(7)

(8)

5) 协方差阵递推Pk|k,i+1：

Pk|k,i+1=(I9-Kk,iHk,i)TPk|k-1

(9)

由上述步骤可以看出，当迭代次数为1的时候，IEKF和EKF是等价的。

2.2 LM-IEKF算法

利用数学方法可以证明IEKF在本质上是和高斯牛顿迭代法等价的[17]，可以看作是高斯牛顿迭代在最大似然估计意义上的近似解。考虑到高斯牛顿在非线性迭代中的表现特点，IEKF在过程噪声或测量噪声过大、运动模型不准确、较大的初始误差等多种情况下，容易出现不稳定[10,18]。据此，本文借鉴了LM方法优化高斯牛顿迭代的思想，对IEKF进行改进，以提高算法的稳定性，实现全局的最优估计。

2.2.1 状态更新方程的推导

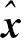
(10)

为了简便，将当前时刻的观测量和状态估计值组成一个增广的观测向量，同理观测矩阵也对应的进行改写：

Z=[z,x0]T，g(x)=[h(x),x]T

(11)

由式(10)可得

(12)

对于高斯牛顿法来说，迭代公式表示为

xi+1=xi-(r′(xi)Tr′(xi))-1r′(xi)Tr(xi)

(13)

基于LM优化的思想[19-20]，将式(13)改进为

xi+1=xi-(r′(xi)Tr′(xi)+μI)-1r′(xi)Tr(xi)

(14)

式中：μ为阻尼因子，决定了迭代的方向和步长。

定义：r(x)=S(Z-g(x))

(15)

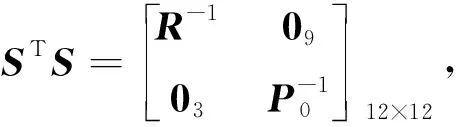
r′(x)=-Sg′(x)

(16)

其中：

(17)

将式(15)、式(16)代入式(14)中，推导出在k时刻的状态变量第i次迭代公式为

xi+1=xi+(g′(xi)TSTSg′(xi)+μI9)-1·

g′(xi)TSTS(Z-g(xi))=xi+

(18)

根据式(17)、式(18)可以进一步推导为

(19)

2.2.2 协方差阵递推公式的推导

根据式(12)的定义，用最大似然函数L(x)表示Z关于变量x的概率密度：

(20)

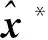
(21)

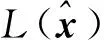
(22)

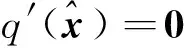
(23)

由线性化近似：

(24)

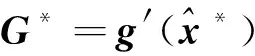
令V=Z-g(x),由式(12)可知,V～(012×1,Q)。

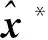
(25)

(26)

G*TQ-1E(VVT)Q-1G*(G*TQ-1G*)-1=

(G*TQ-1G*)-1

(27)

假设第k时刻，当i=n时迭代结束，由式(17) 和式(27)，可得第k时刻迭代结束后，进入到下一时刻k+1的协方差更新公式：

(28)

2.2.3 LM-IEKF算法流程推导

基于2.2.2节关于LM-IEKF算法中的状态更新方程以及基于最大似然估计的协方差阵递推公式的研究。本节推导了算法的整体流程。

1) 设置滤波器的初值xk0、Pk0。

(29)

3) 求一步预测的均方差阵Pk|k-1：

Pk|k-1=Φk-1Pk-1Φk-1T+Qk-1

(30)

4) 设置迭代初值：

(31)

5) 求量测阵的雅克比矩阵Hk,i：

(32)

(33)

7) 求协方差阵的递推值Pk|k,i+1：

(34)

8) 判断终止条件

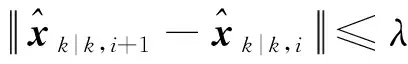
3 包含乘性噪声自适应修正的Modified LM-IEKF算法

当实际环境中包含多种非线性的畸变、信号能量的衰减、运行过程中的抖动等情况时，都会不可避免地引入乘性噪声。本文假设传感器测得的距离值被污染，量测噪声不仅包含有加性噪声，也包含有与距离相关的乘性噪声，并且距离的量测误差假定与传感器至目标之间的距离成线性关系。因此，量测矩阵可写为

(35)

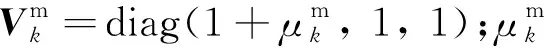
针对与距离相关的乘性噪声，通过储存一段时间Tm内的n个量测噪声残差，并计算量测噪声统计的估计值。自适应修正方法在滤波的算法流程中，一方面对未知的噪声统计参数进行估计，另一方面也利用量测修正状态变量的预测值。

量测噪声的样本方差阵为

(36)

样本方差阵的期望值为

(37)

把式(35)代入式(36)，可以得到量测噪声协方差矩阵的估计值为

(38)

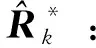
(39)

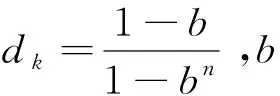
4 实验与分析

为了验证本文提出的LM-IEKF算法和Modified LM-IEKF算法的有效性，本文利用MATLAB采用蒙特卡罗方法，在仅含有加性噪声和包含乘性噪声两种情况下展开仿真与分析，并与EKF和IEKF算法进行了比较。

4.1 仿真条件

设置仿真时间为600 s。设置传感器的精度(3σ)为[30 m, 2 mrad, 2 mrad]，更新频率为2 Hz。设置目标的起始位置为[118.300°， 31.0°， 8 000.0 m]，以100 m/s的速度朝北向匀速直线运动。设置无人机的起始位置为[118.30°, 31.290°, 6 250.0 m]，初始姿态角为[0°, 0°, 0°]，初始速度为[0, 100 ms, ]。无人机的轨迹参数见表1。无人机与目标的轨迹模拟由远及近的会合过程，且无人机包含有平飞、爬升和转弯等机动过程。本文以MAE(Mean Absolute Error)和RMSE(Root Mean Square Error)来评价算法的精度情况。图3为以目标的起始位置为原点的相对位置示意图。图4为仿真设定的无人机与目标之间的相对位置和相对速度(vx,vy,vz)变化的曲线图。

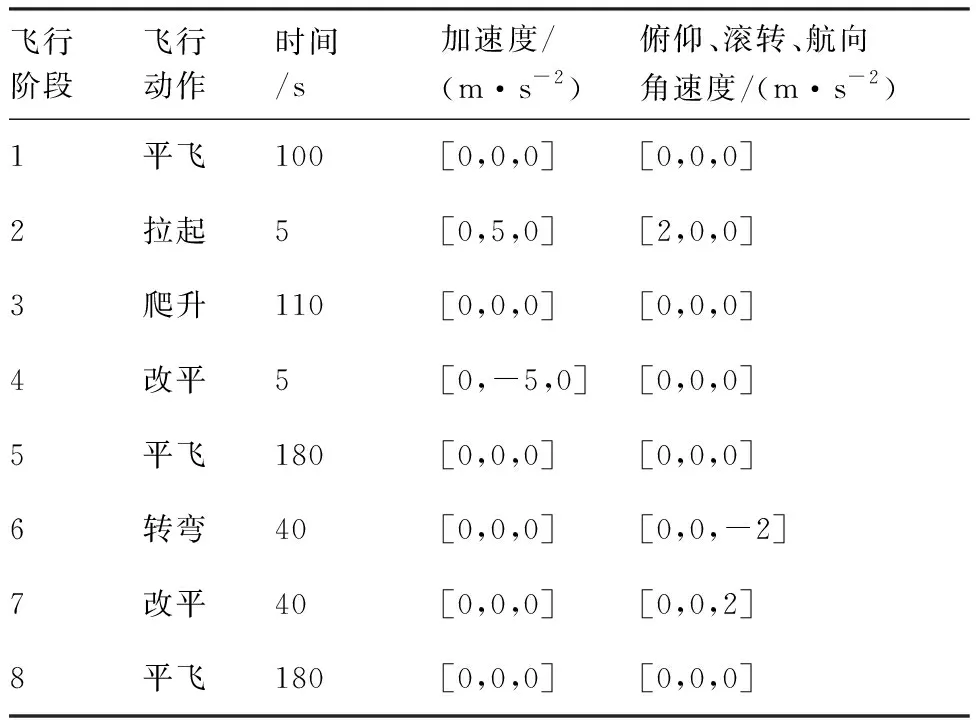
表1 无人机的轨迹参数Table 1 Trajectory parameter of UAV

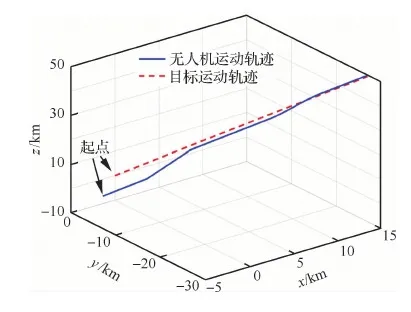
图3 无人机与目标的相对位置示意图Fig.3 Diagram of relative position between UAV and target

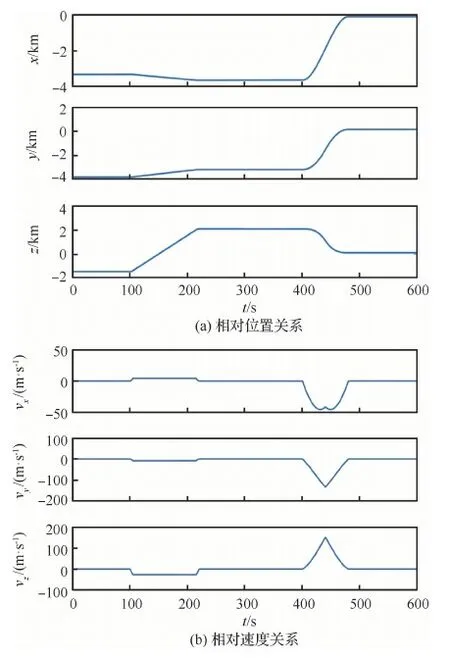
图4 无人机与目标之间的相对位置和速度关系变化曲线Fig.4 Variation of relative position and velocity between UAV and target

4.2 仅含加性噪声情况下的仿真与分析

本节在仅含加性噪声的情况下，考察算法的精度。采用蒙特卡罗方法统计100次运行的结果，通过对每个时刻的100组数据取平均值绘制相对位置的误差曲线如图5(a) 所示，对100组数据求解RMSE值绘制对比曲线如图5(b) 所示。由于LM本质是一种优化迭代过程的数值方法，可以有效地减少陷入局域极值的几率，保证了全局的收敛性，因而也具有更好的稳定性。从图5中初始阶段的局部放大图可以看出，在最初始的一段时间内，LM-IEKF算法的收敛速度是要介于IEKF和EKF之间的，相较于其他两种算法，在性能表现上也显得更为稳健。

图6为相对速度的误差曲线和RMSE对比曲线。从初始段的局部放大图中可以看到，LM-IEKF算法具有更快的收敛速度，在5 s以内可以进入相对稳定的状态，而另外两种算法则要在10 s 左右。并且EKF和IEKF算法在初始段会

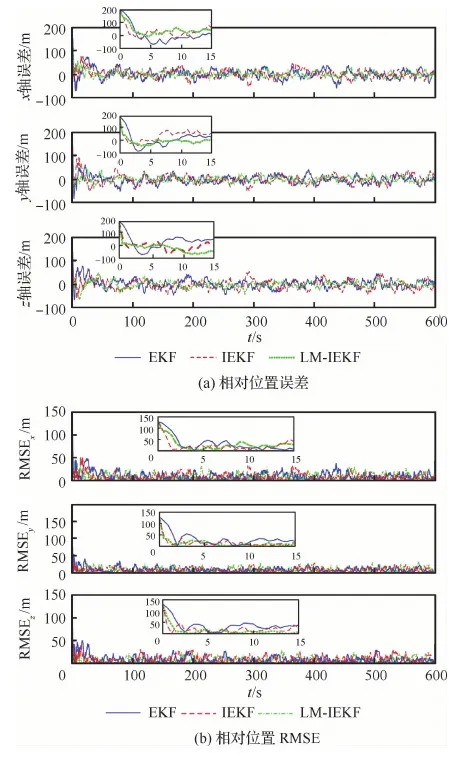
图5 仅含加性噪声情况下的相对位置误差和RMSE曲线Fig.5 Errors and RMSE curves of relative position with additive noise only

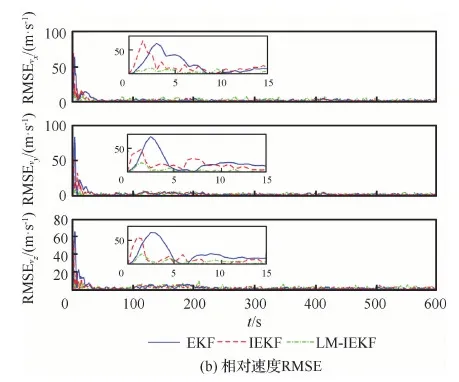
图6 仅含加性噪声情况下的相对速度误差和RMSE曲线Fig.6 Errors and RMSE curves of relative velocity with additive noise only

产生较大的尖峰,相对速度误差达到100 m/s，对比可知LM-IEKF算法具有较好的稳定性。

表2为3种算法对相对导航状态的误差统计，图7(a)为根据表2数据绘制的相对位置精度柱状图，图7(b)为相对速度精度柱状图。从图7的柱状图可以看出，在相对位置和相对速度方面，LM-IEKF要优于其他2种算法。

本文提出的LM-IEKF算法相较于广泛使用的EKF算法，在x、y、z三轴上，相对位置MAE分别减小了32%、30%和31%，相对速度MAE分别减小了25%、37%和17%。在RMSE方面，综合相对位置精度提升了20%，综合相对速度精度提升了46%。

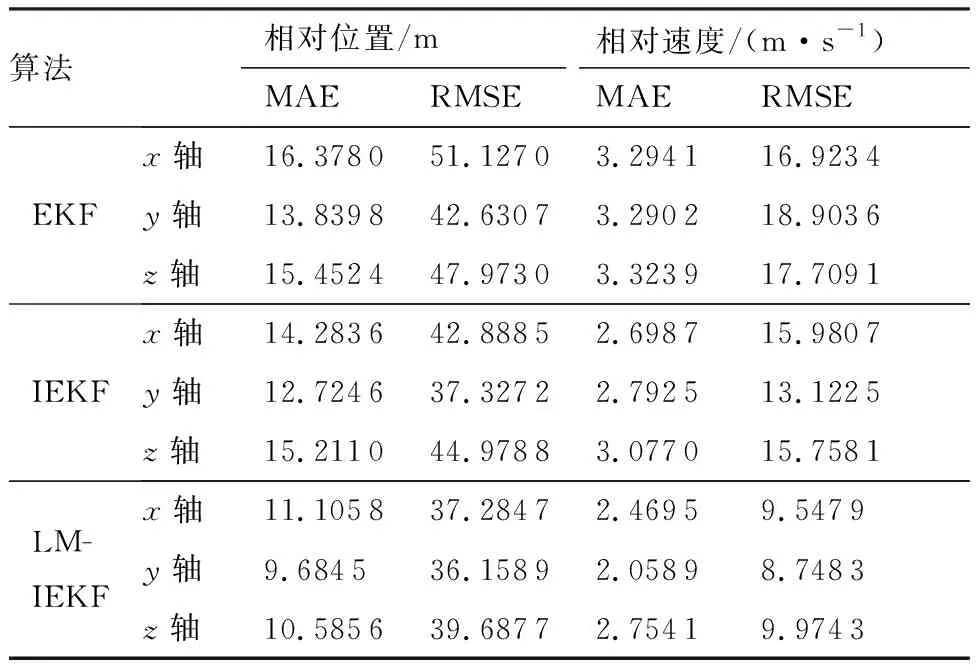
表2 仅含加性噪声情况下的误差统计Table 2 Error statistics with additive noise only

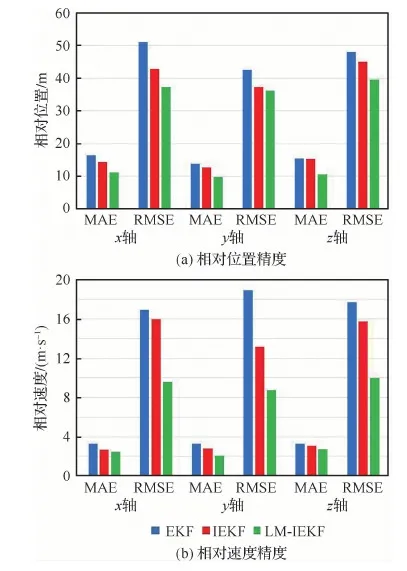
图7 仅含加性噪声情况的相对位置和速度精度柱状图Fig.7 Histogram of relative position and velocity accuracy with additive noise only

4.3 包含乘性噪声情况下的仿真与分析

进一步讨论本文提出的自适应量测噪声修正算法对于乘性噪声的修正效果，考虑到乘性噪声与无人机和目标直线距离之间的线性关系，为了更好地反应出算法对乘性噪声由小到大变化过程的适应性，乘性噪声设置为均值是0.5，方差为4.9×10-3的高斯白噪声[14-15]。Modified LM-IEKF算法的滑动窗口取10 s内的N组数据，N的大小取决于迭代的次数。采用蒙特卡罗方法运行100次进行统计比较。

从图4(a)中可以看出，在x轴和y轴方向上，0～400 s之间为高乘性噪声段，之后随着无人机与目标之间距离的逐渐减小，乘性噪声也逐渐减弱。在z轴方向上，100～200 s之间，乘性噪声经历了由强到弱再至强的变化过程，400 s后随着相对位置逐渐接近，乘性噪声也逐渐衰减。

图8包含乘性噪声情况下的相对位置误差和RMSE曲线图。从图中可以看出，第2节中提出的LM-IEKF算法，有一定的改进效果。本文第3节 中提出的Modified LM-IEKF相较于前面的3种算法可以更好地统计量测噪声，得到更高精度的相对导航状态。

图9为包含乘性噪声情况下的相对速度误差和RMSE曲线图。由430～470 s之间的局部放大图可以看到，在速度机动性较大的阶段，Modified LM-IEKF相较于其他3种算法可以更快的做出响应，在y轴和z轴方向上更为明显。

表3为4种算法在包含乘性噪声情况下的精度对比情况。图10为根据表3数据绘制的相对位置和相对速度精度柱状图。表中数据说明了Modified LM-IEKF算法相较于其他3种算法，在存在乘性噪声污染的情况下，可以较大地提升性能。本文提出的Modified LM-IEKF算法相较于广泛使用的EKF算法，在x、y、z三轴上，相对

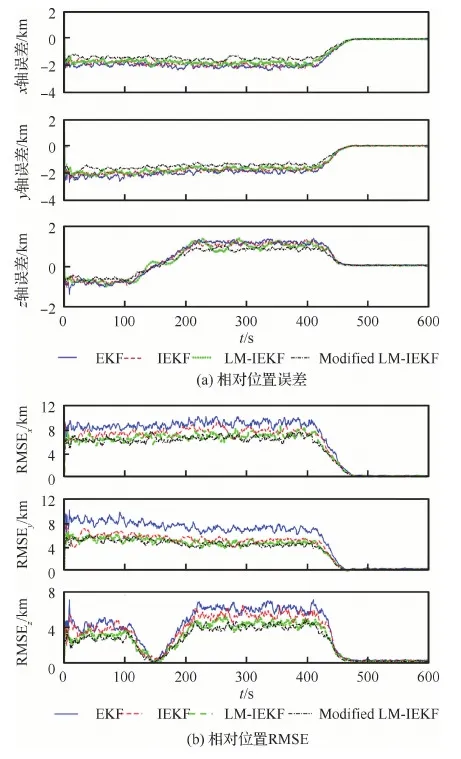
图8 包含乘性噪声的相对位置误差和RMSE曲线Fig.8 Errors and RMSE curves of relative position containing multiplicative noise

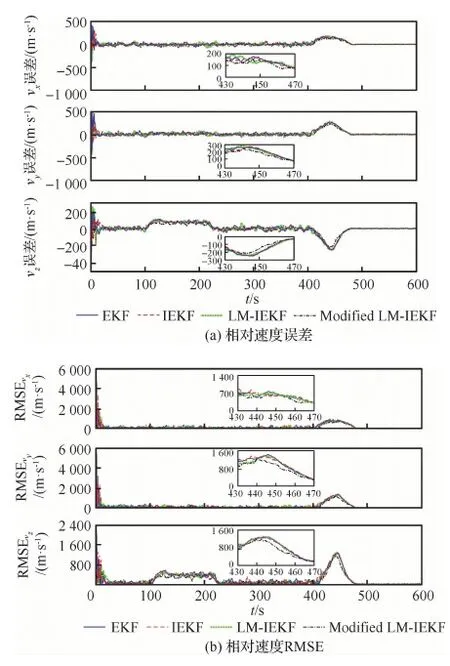
图9 包含乘性噪声的相对速度误差和RMSE曲线Fig.9 Error and RMSE curves of relative velocity containing multiplicative noise

表3 包含乘性噪声情况下的误差统计Table 3 Error statistics containing multiplicative noise

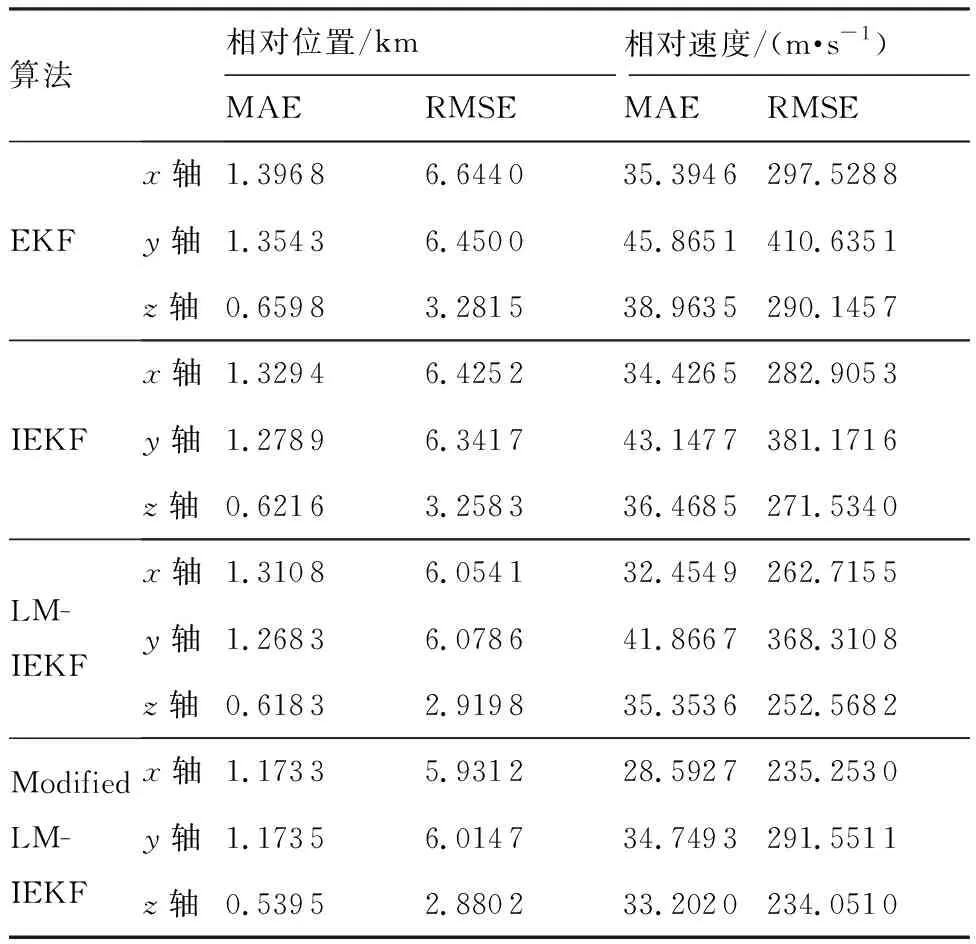
算法相对位置/km相对速度/(m·s-1)MAERMSEMAERMSEEKFx轴1.39686.644035.3946297.5288y轴1.35436.450045.8651410.6351z轴0.65983.281538.9635290.1457IEKFx轴1.32946.425234.4265282.9053y轴1.27896.341743.1477381.1716z轴0.62163.258336.4685271.5340LM-IEKFx轴1.31086.054132.4549262.7155y轴1.26836.078641.8667368.3108z轴0.61832.919835.3536252.5682Modified LM-IEKFx轴1.17335.931228.5927235.2530y轴1.17356.014734.7493291.5511z轴0.53952.880233.2020234.0510

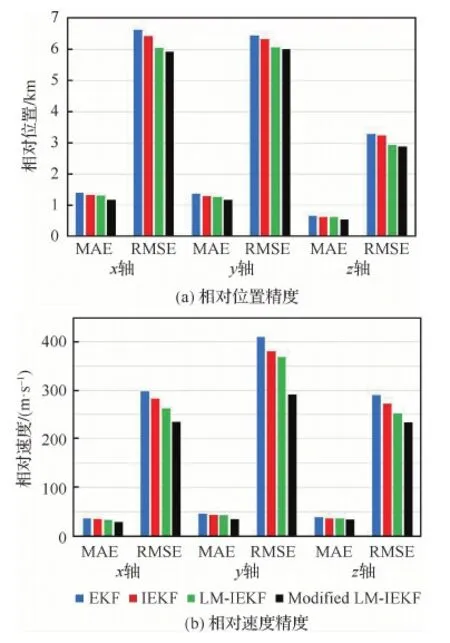
图10 包含乘性噪声情况下的相对位置和速度精度柱状图Fig.10 Histogram of relative position and velocity accuracy containing multiplicative noise

位置MAE分别减小了16%、13%和18%，相对速度MAE分别减小了34%、23%和14%。在RMSE方面，综合相对位置精度提升了10%，综合相对速度精度提升了23%。

5 结 论

1) 本文针对无人机与非合作目标之间的中远距相对导航问题，提出了一种LM-IEKF相对状态估计算法。该算法利用了Levenberg-Marquardt优化的思想改进IEKF中的迭代过程，以提高滤波器的精度和稳定性。通过计算对比分析结果可知：在仅含加性噪声情况下，LM-IEKF算法相较于EKF、IEKF具有更好的性能。

2) 考虑到距离传感器因信号相关特性所引入的乘性噪声，进一步提出了基于量测噪声自适应修正地Modified LM-IEKF算法。通过对比分析：在包含乘性噪声的情况下，Modified LM-IEKF算法可以有效的在线估计量测噪声，在提高相对导航状态估计精度方面优于其他算法。与目前广泛使用的EKF算法相比，在综合相对位置精度上提高了10%，在综合相对速度精度上提升了23%。

上述研究成果对于无人机在民用、军用等领域的发展具有一定的参考价值。