求解最优月球软着陆轨道的隐式打靶法

彭坤，彭睿，黄震，张柏楠

1.中国空间技术研究院 载人航天总体部，北京 100094 2.北京航空航天大学，北京 100083

近年来，各航天大国纷纷将月球探测与开发作为研究重点[1-2]。而实施月球软着陆是月球资源开发、原位资源利用以及载人登月任务的基础。月球软着陆过程一般分为霍曼转移段和动力下降段[3-4]，其中动力下降段会消耗大量燃料，因此需设计燃料消耗最优动力下降段着陆轨道。

月球软着陆轨道设计是一种终端时刻自由的最优控制问题，其主要求解方法分为3大类[5-6]：间接法、直接法和混合法。间接法是最早用来求解月球软着陆轨道的方法，其利用庞特亚金极大值原理将最优控制问题转化为两点边值问题进行求解[7]。该方法的不足是两点边值问题的求解会因初值敏感而很难收敛。更多的学者应用直接法求解月球软着陆轨道，利用配点法[8-9]、函数逼近方法[10-11]以及伪谱法[12-14]将轨道状态变量和控制变量离散化并作为优化变量，再采用序列二次规划或智能寻优算法进行求解。直接法虽然收敛性好，但其求解时间随计算精度的提高而增加；同时其是一种次优解法，燃料消耗非最优。混合法则利用间接法的最优控制律，将伴随变量初值作为优化变量，采用非线性规划[15]或智能优化算法[16-17]进行求解。其求解结果相比于直接法更接近最优解，同时计算量小；相比于间接法降低了初值敏感性。但混合法的寻优时间仍远高于间接法的迭代求解时间，同时其舍弃了部分最优性条件，求解结果不能严格保证最优性，还需要与间接法结果进行比对。因此，只有间接法能求得理论最优解，同时其一旦能收敛，求解速度最快，计算精度最高。

为此，学者们开始重新研究通过间接法来求解最优月球软着陆轨道问题，研究重点是对终端时刻的修正和收敛性强的两点边值问题求解方法。赵吉松等[18]采用线性摄动法[19]同时对伴随变量初值和终端时刻进行修正。肖尧等[20]引入一种时间尺度变换方法[21]来解决终端时刻自由问题，借用MATLAB的bvp4c函数求解月球软着陆两点边值问题。

为提高求解两点边值问题的收敛性，本文建立了月球软着陆的归一化系统模型，减少状态变量之间和伴随变量之间的量级差距。同时，采用时间尺度变换方法将终端时刻自由问题转化为时间区间为[0,1]的终端时刻固定问题。进而把终端时刻看作状态变量并引入哈密尔顿函数终端值作为隐式终端条件，将原显式终端条件的两点边值问题转化为隐式终端条件的两点边值问题。最后，采用变分法对隐式终端条件进行处理，提出一种隐式打靶法并对该问题进行求解，得到燃料消耗最优的月球软着陆轨道，并分析了月球软着陆过程中燃料消耗与着陆器发动机推重比之间的关系。

1 系统模型

忽略动力下降段的横向偏差，采用二维极坐标系描述月球软着陆过程，并以初始时刻月面着陆器的月心距和质量为参考量，可建立月球软着陆过程的归一化状态方程为[17]

(1)

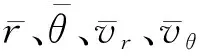
(2)

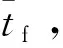
(3)

(4)

设月球软着陆过程发动机一直开机，则月面着陆器的燃料消耗与飞行时间成正比，故可设性能指标为

(5)

2 隐式终端条件两点边值问题

2.1 最优控制问题向两点边值问题的转化

利用庞特亚金极大值原理可得哈密尔顿函数H为

(6)

1) 最优推力方向角u控制律为

tanu=(-λvr)/(-λvθ)

(7)

2) 伴随变量方程为

(8)

3) 由横截条件[22]可推导出终端条件为

(9)

(10)

两点边值问题的边界条件为

(11)

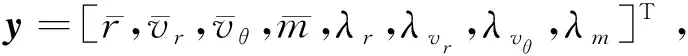
2.2 显式终端条件向隐式终端条件的转化

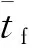
(12)

(13)

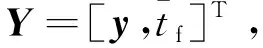
(14)

该边界条件的最后一个终端约束与其他终端约束不同，它不是某个状态变量的终端值，而是包含某些状态变量的一个等式约束，属于隐式终端条件。

3 隐式打靶法

3.1 隐式终端条件处理

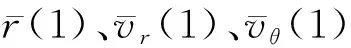
(15)

隐式终端条件可简单表示为

(16)

定义g(1)的变分[22]为

δg(1)=g*(1)-g(1)=-g(1)

(17)

式中：g*(1)为终端约束的真值，即g*(1)=0;g(1)为迭代计算值，存在误差。另一方面，通过变分法则可得

(18)

式中：

(19)

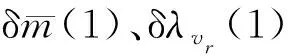
(20)

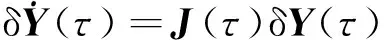
(21)

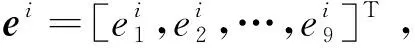
(22)

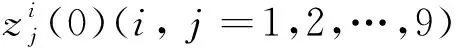
A5x0=-g(1)

(23)

式中：

(24)

通过共轭函数法还可得到4个显式终端条件的关系式，再加入式(23)可得

(25)

式中：

(26)

(27)

3.2 算法流程

隐式打靶法求解月球软着陆轨道两点边值问题的步骤如下：

3) 判断终止条件

(28)

是否满足，若满足，则停止迭代；若满足第1分式，则求得最优解Y*(τ)=Y(k)(τ)；若满足第2分式，则迭代失败，输出失败信息。否则，转第4)步。

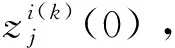
(29)

4 仿真验证

月球软着陆初始条件[10]为r0=1 753 km,θ0=0°,vr0=0 m/s,vθ0=(9.65×10-4·r0)m/s。终端约束为rf=1 738 km,vrf=0 m/s,vθf=0 m/s。月球引力常数为μL=4.902 75×1012m3/s2。以载人月面着陆器为例，设着陆器质量为m0=18 t，发动机推力为Ft=50 000 N，排气速度为w=310×9.8 m/s。

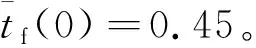
由表1可知，隐式打靶法可以搜索到最优月球软着陆轨道，收敛精度高，归一化的终端约束精度可以达到10-10量级，且收敛时间短，仅为1 s左右。最终求得的载人月面着陆器的月球软着陆过程总时间为486.5 s，燃料消耗为8 007.719 kg。图1 给出了归一化系统模型中4个状态变量的变化曲线，图2给出了对应的4个伴随变量的变化曲线，图3给出了软着陆过程中推力方向角的变化曲线，图4给出了间接法构造的哈密尔顿函数的变化曲线。由图1可知，所求得的轨道严格满足软着陆的月心距、径向速度、横向速度约束。由图2和图4可知，所求得的轨道严格满足间接法的式(9)的横截条件要求，证明了其最优性。同时由图2可知，由于系统模型的归一化处理，伴随变量的量级相差较小，更有利于问题求解过程的收敛。由图3可知，推力方向角初始值在180°左右，说明λvr(0)<0和λvθ(0)>0，且|λvθ(0)|≥|λvr(0)|，验证了初值猜测的合理性。

将隐式打靶法与直接法和混合法进行对比分析。直接法采用文献[10]的插值函数逼近法将控制函数参数化，将燃料消耗作为性能指标，终端目标约束作为惩罚项，采用人工免疫算法进行求解。混合法采用文献[17]的方法，将伴随变量初值和飞行时间作为控制变量，评价函数与直接法相同，也采用人工免疫算法进行求解。3种方法的求解结果如表2所示。由表可看出，隐式打靶法的终端约束误差比直接法和混合法小4～6个数量级，收敛时间也比直接法和混合法低2～3个数量级。直接法求解的燃料消耗大于隐式打靶法和混合法。混合法由于控制律与隐式打靶法相同，优化结果接近隐式打靶法结果。混合法求解时将终端约束设为评价函数的惩罚项予以考虑，用随机搜索算法人工免疫算法进行搜索，在前期搜索中能快速收敛到最优解附近，但在后期搜索中局部收敛过程比较慢，无法将终端约束误差控制得特别低。而隐式打靶法直接通过终端约束误差修正控制变量，可以得到较低误差的终端约束，故收敛精度高于混合法。

表1 隐式打靶法搜索结果Table 1 Search results of implicit shooting method

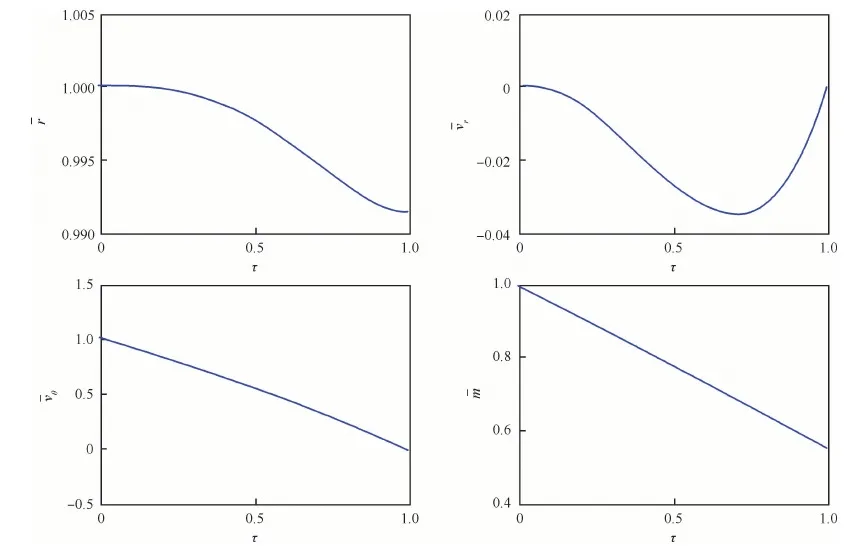
图1 归一化状态变量随时间变化曲线Fig.1 Temporal variation curves of normalization state variables

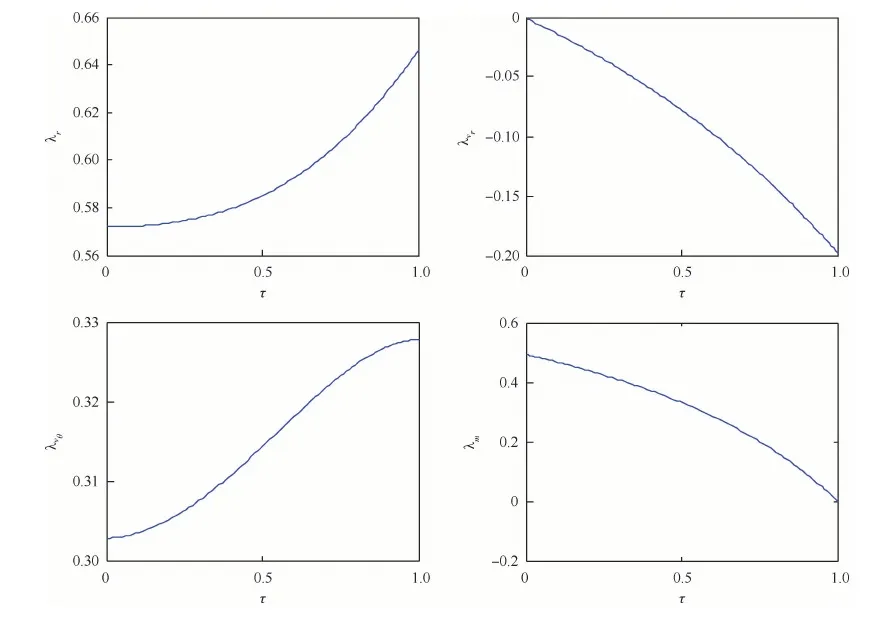
图2 伴随变量随时间变化曲线Fig.2 Temporal variation curves of adjoint variables

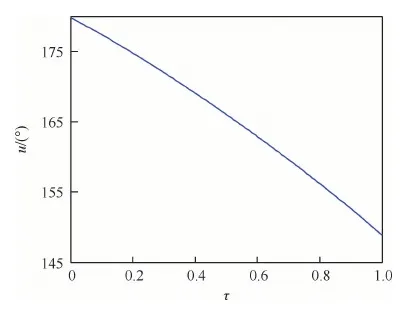
图3 推力方向角随时间变化曲线Fig.3 Temporal variation curves of thrust direction angle

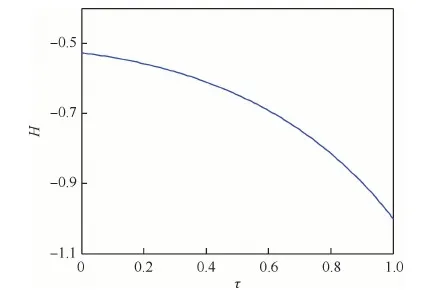
图4 哈密尔顿函数随时间变化曲线Fig.4 Temporal variation curves of Hamiltonian function

表2 隐式打靶法与直接法和混合法搜索结果对比Table 2 Comparisons of search results of implicit shooting method with direct method and hybrid method

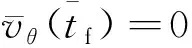
为进一步验证隐式打靶法的收敛性，对η∈[0.1, 1.0](η=Ft/(m0g)为发动机推重比，g为

表3 隐式打靶法与显式打靶法搜索结果对比

Table 3 Comparisons of search results of implicit shooting method with explicit shooting method

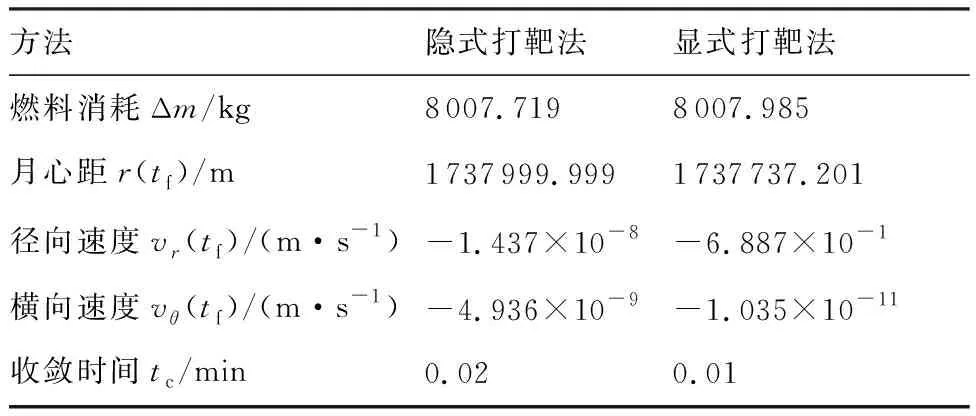
方法隐式打靶法显式打靶法燃料消耗Δm/kg8007.7198007.985月心距r(tf)/m1737999.9991737737.201径向速度vr(tf)/(m·s-1)-1.437×10-8-6.887×10-1横向速度vθ(tf)/(m·s-1)-4.936×10-9-1.035×10-11收敛时间tc/min0.020.01

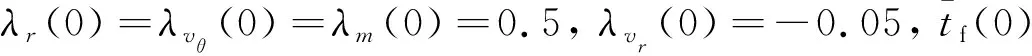
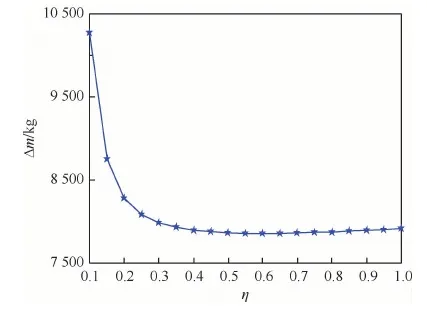
图5 燃料消耗随推重比变化曲线Fig.5 Variation curve of fuel consumption with thrust-weight ratio

5 结 论

1) 时间尺度变换法和本文推导的隐式打靶法的组合能够快速而精确地求解出终端时刻自由的最优月球软着陆轨道，与直接法和混合法相比，隐式打靶法优化精度高，收敛速度快。

2) 系统模型的归一化处理减小了伴随变量的量级差，进而缩小了伴随变量的猜测范围，同时结合隐式打靶法中伴随变量初值和终端时刻的联合修正，大大降低了迭代过程的敏感性，从而提高了间接法的收敛性。

3) 本文提出的隐式打靶法收敛性强，可适应参数值大范围变化的月球软着陆问题求解，也可应用于其他终端时刻自由的轨道优化问题求解。

4) 对于最优月球软着陆轨道，推重比η∈[0.1,1.0]时，燃料消耗随推重比增加先急剧减小后缓慢增大，推重比为0.6时燃料消耗最小，该变化趋势可为载人月面着陆器下降级发动机选型提供参考。