双重未知干扰解耦的多传感器系统偏差校正与状态估计

冯肖雪，李淑慧,*，潘峰, 2

1. 北京理工大学 自动化学院，北京 100081 2. 北京理工大学 昆明产业技术研究院，昆明 6501064

传感器可以提供感兴趣目标在时间和空间上的信息，因而在目标跟踪、组合导航、容错控制以及工业监控等领域应用十分广泛，其中传感系统的状态估计问题日益引起人们的关注。但是在状态估计过程中，由于系统参数的变动、大型系统中的相互耦合项、系统动态学中的非线性项、传感器测量精度有限等因素引起系统建模模型误差，往往影响状态估计精度。一般而言，可将上述几类引起建模误差的因素统一视为未知干扰输入。具有未知干扰输入的随机系统状态估计问题广泛存在于控制、通信、信号处理和故障诊断等领域。目前解决含有未知干扰输入的随机系统状态估计问题的方法，大致可以分为以下几类。

1) 状态方程中含有未知干扰：文献[1]针对直流电动机的状态估计和故障诊断问题，通过解耦未知干扰输入，借鉴递归滤波器的框架提出了鲁棒的三步卡尔曼滤波算法，实现了最小方差无偏状态估计和故障诊断。文献[2]针对含有未知干扰、执行器和传感器故障的离散线性系统，基于鲁棒两阶滤波器估计状态、生成观测冗余，进而采用贝叶斯二值假设检验自适应地诊断故障。但上述方法为实现未知干扰解耦对故障反馈矩阵的秩有着严格的约束条件。文献[3]针对状态方程中含有未知干扰的线性时变随机系统联合状态估计与故障诊断问题，通过将复杂不确定系统转换为标准的带故障和未知输入的状态空间模型，基于最小方差无偏准则提出了递归五步滤波器来估计系统的状态和故障，该算法对于故障反馈矩阵的秩没有任何约束限制，但估计结果并非最优。参考文献[4]针对状态方程含有未知干扰的不确定广义系统，通过将未知干扰扩维到状态向量中推导了最优递归滤波器，但是该方法计算量大，实时性无法得到保证。

2) 量测方程中含有未知干扰：文献[5]针对传感器含未知输入和相关噪声的离散随机线性系统，设计了最小方差无偏状态估计器，推导了任意两个传感器子系统之间的滤波误差互协方差矩阵，给出了标量加权分布式融合状态滤波器。文献[6]研究了含有量测丢失和未知量测干扰的多传感器随机不确定性系统，设计了独立于未知干扰的集中/分布式融合状态估计器，但上述两种方法均要求随机干扰矩阵的秩不得超过传感器量测维数。文献[7]针对量测方程中含有未知干扰的线性时变系统设计了上界滤波器，通过凸优化求解滤波上界的极小值获得了最优参数估计结果，但该方法要求量测新息协方差存在上界。

3)状态和量测方程中均含有未知干扰：文献[8] 将未知干扰简化为均值和方差未知的高斯项，对未知干扰与状态不独立情况下的离散随机系统提出了两阶期望最大化算法来辨识未知干扰。文献[9]基于期望极大化方法提出了联合状态估计和未知输入辨识的框架，用来计算系统未知输入的条件期望，但该方法同样假设未知干扰服从高斯分布。文献[10]针对含有未知干扰的线性时变离散随机系统，提出了扩维鲁棒三阶卡尔曼滤波对系统状态和故障进行同时估计。文献[11]针对含有未知干扰、执行器故障和传感器故障的线性时变离散随机系统的故障诊断和状态估计问题，提出了改进的增广鲁棒三阶卡尔曼滤波算法，但上述两种算法均假设未知干扰建模为宽平稳过程的随机游走噪声。

总结来看，针对状态和量测方程中含有未知干扰的状态估计问题，目前的相关研究成果存在以下局限性：① 算法推导过程中对部分变量有着严格的假设或约束条件；② 通常假设未知干扰输入具有高斯特性或者具有确定的分布特性；③ 通过归并、扩维等方法对未知干扰进行估计，算法非实时、复杂度高。因此，很有必要研究状态方程含有未知干扰(无任何先验信息)、量测方程含有未知偏差(可视为一类特定的干扰)情况下的多传感器在线状态估计问题。

本文设计了适用于状态方程含未知干扰、量测方程含未知偏差的多传感器最小方差无偏估计滤波器。组织结构如下：第1节描述了状态方程含未知干扰、量测方程含未知偏差的动态离散系统，并给出了本文研究的问题。第2节针对状态方程含未知干扰、量测方程含有未知偏差的动态离散系统设计了双重未知干扰解耦下的最小方差无偏估计滤波器。第3节给出了径向飞行控制系统的仿真实例验证了本文提出算法的有效性。第4 节对论文工作进行了总结。

1 问题提出

状态方程和量测方程带有未知干扰输入影响的线性离散系统可描述为

xk+1=Akxk+Bkμk+ζk+Ekdk

(1)

yi,k=Ci,kxk+ηi,k+Di,kbi,k

(2)

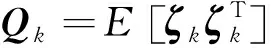
式(2)通过Di,kbi,k项来描述各种不同的传感器量测建模不确定性。不失一般性，可以对未知的传感器干扰或者偏差给出如下演化模型:

bi,k+1=Fi,kbi,k+vi,k+Gi,kui,k

(3)

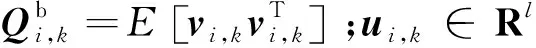
说明1 不失一般性，认为Ek为列满秩矩阵。因为即便Ek不满足列满秩，依然可通过秩分解，Ekdk=E1,kE2,kdk，令第1项E1,k为列满秩矩阵，而利用Ci,k+1来描述状态模型所受的未知干扰输入。通过Ekdk项除了可以描述加性干扰外，还可以用来描述各种不同的系统状态建模不确定性，比如系统建模过程中的非线性项、线性化操作、模型降阶简化、以及参数变化等引入的误差。

说明2 式(3)中定义的传感器干扰或者偏差演变模型是普遍意义上的通用模型。若Fi,k=I,vi,k=0,Gi,k=0，则传感器干扰或偏差为常值；若Fi,k=0,Gi,k=0，则传感器干扰或偏差为服从零均值高斯分布的随机值；若Fi,k≠0,Gi,k=0，则传感器干扰或偏差模型为常见的时变系统；若Gi,k≠0，则该演化模型可描述传感器偏差或干扰受到未知输入的影响，比如突发的阶跃信号输入等。

说明3 参考文献[12]中指出，可以通过对传感器输出信号进行变换使其干扰项变为零，即进行传感器量测方程中的干扰或者偏差解耦，进而将量测方程受输入干扰的滤波器设计转化为传统的无干扰量测系统滤波器求解问题。文献[13-14]针对含有时不变的未知干扰输入的系统设计了未知干扰解耦最优观测器，文献[15-16]针对一类不含随机噪声的具有未知干扰或输入的线性系统设计了未知输入观测器。但是本文研究的未知干扰输入是时变的，同时传感器量测受到随机噪声的污染，因此文献[12-16]中的相关算法并不适用于本文。此外，本文中传感器受到的干扰或者偏差bi,k是无法避免的，因为这是进一步求解状态估计的前提，不进行传感器量测值的校准，将导致状态估计发生严重偏差甚至发散。

本论文的目的是设计适用于状态方程含未知干扰、量测方程含未知偏差影响下的动态随机离散系统最小方差无偏估计滤波器。

2 双重未知干扰解耦状态估计器

本文针对状态方程含未知干扰、量测方程含未知偏差的线性离散系统拟设计一种双重未知干扰解耦下的最小方差无偏估计滤波器来估计多传感器系统的状态。最小方差无偏估计滤波器的设计主要包括两步，第1步是设计传感器量测偏差的最小方差无偏估计器：首先建立传感器量测偏差系统模型，解耦线性离散系统方程中的未知干扰，然后设计最小方差无偏估计器，估计出量测偏差，进而校正动态系统测量值；第2步是设计未知干扰影响下线性离散系统的最优状态观测器：根据量测偏差校正系统测量值，然后对量测干扰偏差校正后的系统设计最优状态观测器，进而获得具有最小方差无偏意义下的状态估计，算法设计框架如图1所示。

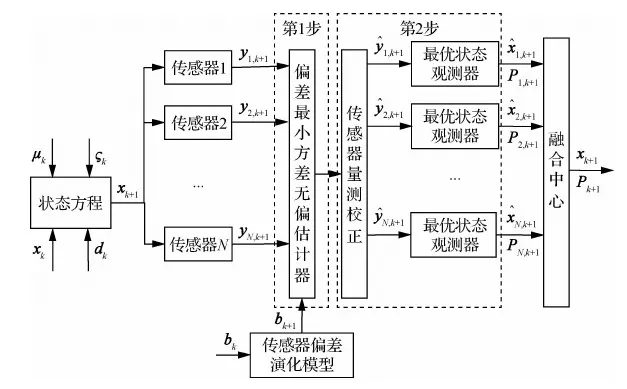
图1 所提算法设计流程图Fig.1 Flow chart of proposed algorithm

2.1 量测偏差最优估计器设计

2.1.1 量测偏差系统模型

将式(1)代入式(2)，得到k+1时刻第i个传感器的量测方程为

yi,k+1=Ci,k+1xk+1+ηi,k+1+Di,k+1bi,k+1=

Ci,k+1(Akxk+Bkμk+ζk+Ekdk)+

ηi,k+1+Di,k+1bi,k+1

(4)

利用传感器量测方程和传感器偏差演变方程可以构造传感器偏差系统模型，即对N个传感器的量测进行线性组合，可得偏差系统模型为

q1y1,k+1)=(CN,k+1-qN-1CN-1,k+1-…-

q1C1,k+1)(Akxk+Bkμk+ζk+Ekdk)+

(ηN,k+1-qN-1ηN-1,k+1-…-q1η1,k+1)+

(DN,k+1bN,k+1-qN-1DN-1,k+1bN-1,k+1-…

-q1D1,k+1b1,k+1)

(5)

式中：qi∈R (i=1,2,…,N-1)为第i个传感器的加权系数，并且0≤qi≤1。为了实现上述构造的偏差系统模型与目标状态解耦，需要消除目标状态信息，即式(5)中的第1项系数应为0，即

CN,k+1-qN-1CN-1,k+1-…-q1C1,k+1=0

(6)

此时，式(5)可写为如下形式，定义为偏差系统模型的量测方程：

(DN,k+1bN,k+1-qN-1DN-1,k+1bN-1,k+1-…

-q1D1,k+1b1,k+1)=Hk+1bk+1+wk+1

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

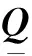
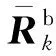
将式(3)中N个传感器的系统偏差改为扩维的形式：

(15)

式中：

综合式(7)与式(15)便构成了系统偏差模型。基于该模型，下面设计解耦滤波器进行系统偏差估计。

2.1.2 未知输入解耦的量测偏差估计器设计

依据2.1.1节给出的偏差系统模型，本节给出一种基于最小方差无偏准则的量测偏差估计方法。该方法首先将量测偏差的未知输入部分进行解耦，使偏差与未知输入无关；随后，基于解耦后的偏差系统模型设计一个最小方差无偏估计器。

(16)

式中:

证明：见附录A。

定理2 基于式(7)与式(16)，可得最小方差无偏估计滤波器为

(17)

(18)

(19)

(20)

(21)

证明：见附录B。

2.2 未知干扰解耦的最优状态观测器设计

传感器偏差校正后的动态系统模型为

(22)

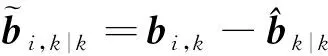
(23)

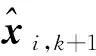
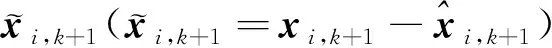
(24)

(25)

(26)

(27)

(28)

Mi,k+1=Ek(Ci,k+1Ek)†

(29)

Ti,k+1=I-Mi,k+1Ci,k+1

(30)

证明：见附录C。

(31)

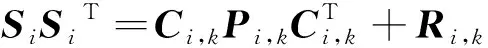
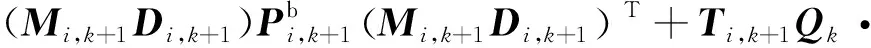
(32)

证明：见附录D。

基于简单凸组合融合算法实现N个传感器的状态融合：

(33)

2.3 所提方法实现步骤

基于2.1节和2.2节的推导和证明，针对多传感器线性离散系统，本文所提的双重未知干扰解耦的最小方差无偏估计滤波器的计算步骤如表1所示。

表1 双重未知干扰解耦下的状态估计滤波器

Table 1 Minimum variance and unbiased estimate filter with dual-decoupling unknown interference

%未知输入解耦下的量测偏差最小方差无偏估计器1.按照式(8)～式(14)计算Hk+1、Q-、B-、bk、wk+1、Λ、Rbk得到偏差系统模型的量测式(7)。2.按照式(15)计算Fbk、Gbk、uk、bk、νbk、Qbk,得到偏差系统模型的状态方程。3.按照式(16)计算Gbk+1、Fbk+1、Γbk+1。4.按照式(17)～式(21)分别计算^bk+1|k、Pbk+1|k、Κbk+1、^bk+1|k+1、Pbk+1|k+1。%未知干扰解耦下的系统状态最小方差无偏估计器5.按照式(24)～式(30)分别计算Δ1i,k+1、Δ2i,k+1、Δi,k+1、A1i,k+1、Li,k+1、Mi,k+1、Ti,k+1。8.按照式(23)计算^xi,k+1、zi,k+1。9.按照式(32)计算Pi,k+1。10.按照式(33)进行状态和协方差估计xk+1、Pxk+1。11.设置k=k+1,转步骤1。

3 实验仿真部分

飞行器径向飞行控制系统简化后的线性离散时间系统模型[12]为

xk+1=Akxk+Bkμk+ζk+Ekdk

Ekdk=ΔAkxk+ΔBkμk=

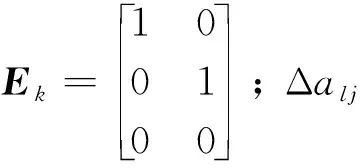
本文分别采用两组加速度计和垂直陀螺仪来测量飞行速度、俯角和俯角率，系统量测方程为

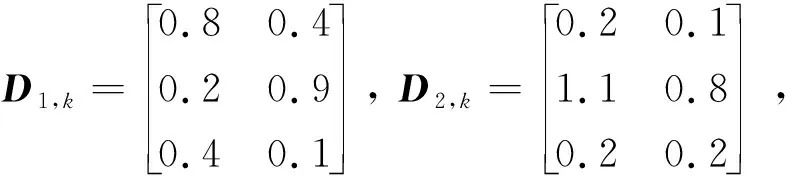
3.1 量测偏差估计结果及分析

本节对所提出的未知输入解耦的量测偏差最小方差无偏估计器的有效性进行验证。图2和图3 给出了与广义最小二乘(Generalized Least Square, GLS)[17]和卡尔曼滤波(Kalman Filter, KF)[18]两个方法的量测偏差估计结果对比。从图2和图3可以看出本文所提方法(Decoupled method)由于对传感器偏差的未知输入进行了解耦设计，进而基于传感器偏差动态演化模型可以很好地跟踪上两个传感器各个维度上的动态偏差值，这反映了本文提出的量测偏差最小方差无偏估计器的有效性。同样基于动态模型估计的KF方法由于忽略了偏差动态演化模型中的未知输入部分，而导致估计效果不佳。基于量测信息估计的GLS方法，不需要利用偏差动态演化模型，仅利用包含了系统偏差未知输入的全部测量信息，因此估计效果基本可以接受，但相比本文所提的Decoupled method仍有较大差距。

为了更清晰地对比3种方法的估计性能，图4 和图5给出了100次蒙特卡罗仿真下两个传感器各个维度上的量测偏差估计RMSEs。可以看出本文所提Decoupled method在两个传感器各个维度上的量测偏差估计RMSEs最小，而KF方法和GLS方法在偏差由于未知输入而发生突变时估计结果有较大波动。同时表2给出了不同算法偏差估计性能比较，可以看出本文所提的Decoupled method的平均RMSEs，相比基于量测信息估计的GLS方法至少提升了6.5%的性能，相比基于模型估计的KF方法至少提升了17%的性能，这验证了本文所提Decoupled method方法在处理带有未知输入干扰下的传感器偏差估计问题上明显的优越性。从运算时间上可以看出，本文所提的Decoupled method相比其他两个方法计算复杂度仅有略微的增加，这是可以接受的。

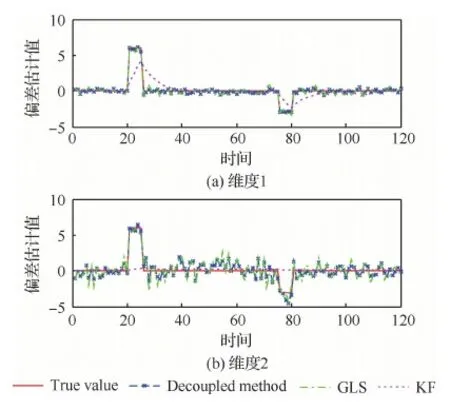
图2 传感器1量测偏差估计方法对比Fig.2 Comparison of bias estimate methods in Sensor 1

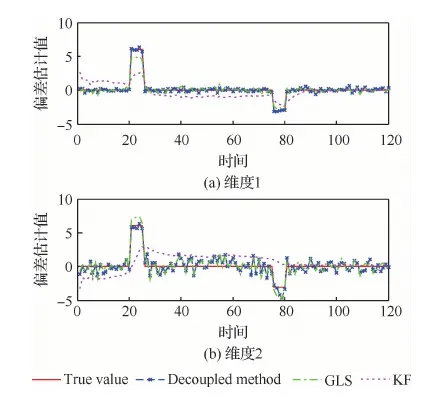
图3 传感器2量测偏差估计方法对比Fig.3 Comparison of bias estimate method in Sensor 2

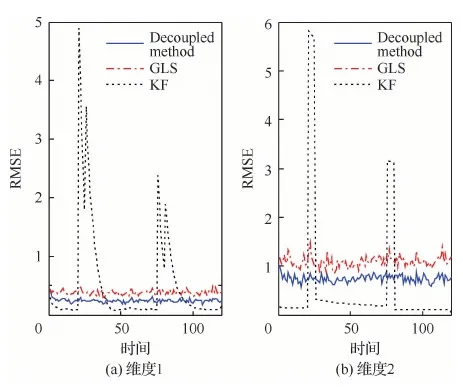
图4 传感器1量测偏差估计RMSEs对比Fig.4 Comparison of bias estimate RMSEs in Sensor 1

图5 传感器2量测偏差估计的RMSEs对比Fig.5 Comparison of bias estimate RMSEs in Sensor 2

表2 不同方法量测偏差估计性能比较Table 2 Comparison of performance of bias estimate

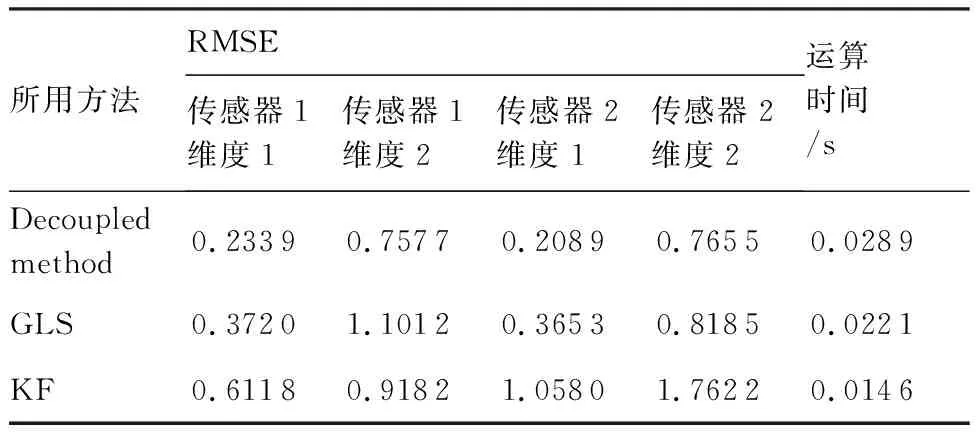
所用方法RMSE传感器1维度1传感器1维度2传感器2维度1传感器2维度2运算时间/sDecoupledmethod0.23390.75770.20890.76550.0289GLS0.37201.10120.36530.81850.0221KF0.61180.91821.05801.76220.0146

3.2 系统状态估计结果及分析

本节对所提出的未知干扰解耦下的系统状态最小方差无偏估计器的有效性进行验证，并与未进行干扰解耦的联邦卡尔曼滤波器[19](Federated Kalman Filter, FKF)和未进行传感器偏差校正的方法(Decoupled method without Bias Compensation, DMBC)进行对比。图6为不同方法在单次仿真下多传感器状态估计结果对比图。可以看出DMBC方法由于未进行传感器偏差补偿，导致在传感器偏差发生突变时不能正确地进行状态估计，而FKF方法由于未考虑状态演化模型中的未知输入部分，导致整体估计效果不佳。而本文所提的Decoupled method不仅对状态演化模型中的未知输入进行解耦设计，同时对传感器偏差进行补偿，因此本文提出的最小方差无偏估计器估计结果更贴近真实的系统状态，这进一步验证了本文提出方法的有效性。

为了更清晰地对比3种方法的估计性能，图7 给出了不同方法在100次蒙特卡罗仿真下状态估计RMSEs结果对比。表3给出了不同方法状态估计平均RMSEs以及运算时间的统计结果。可以看出，本文所提的Decoupled method方法在动态系统状态3个分量(俯仰角，俯仰角速度，速度)的RMSEs都明显优于其他2种方法。本文所提Decoupled method方法相比DMBC方法至少提升了17%的估计性能，相比FKF方法至少提升了65%的估计性能，这进一步反映了本文所提的未知干扰解耦下的系统状态最小方差无偏估计器的优越性。同时值得说明的是，本文所提Decoupled method方法的运算时间是最长的，是以牺牲计算量为代价来换取估计性能的提升。

图6 有/无偏差补偿下状态估计结果Fig.6 State estimate results with and without bias compensation

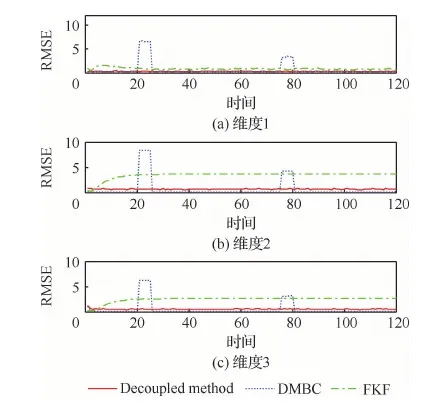
图7 有/无偏差补偿下状态估计RMSEsFig.7 State estimate RMSEs with and without Bias compensation

表3 不同方法状态估计性能比较

Table 3 Comparison of performance of state estimate using different method

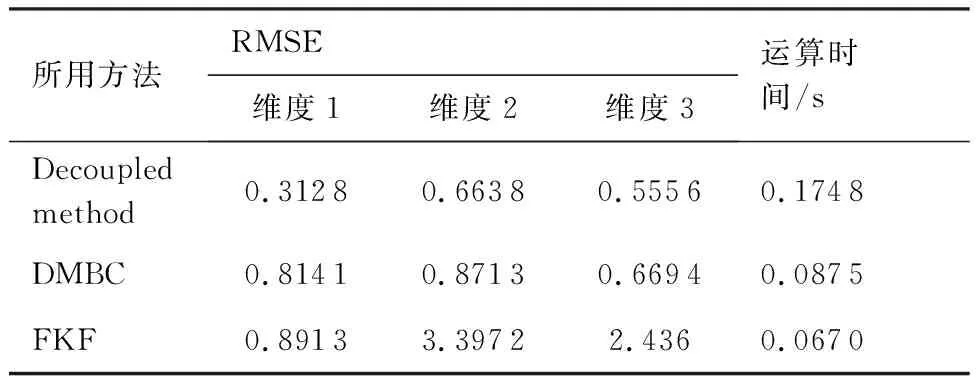
所用方法RMSE维度1维度2维度3运算时间/sDecoupled method0.31280.66380.55560.1748DMBC0.81410.87130.66940.0875FKF0.89133.39722.4360.0670

4 结 论

本文针对状态方程含有未知干扰、量测方程含有未知偏差情况下的多传感器状态估计问题开展了研究，得到如下结论:

1) 基于量测偏差通用演化模型实现了偏差演化模型中的未知输入解耦，进而设计了最小方差无偏估计器对量测干扰偏差进行估计。

2) 利用估计出的量测偏差进行动态系统测量值校正，根据量测干扰偏差校正后的系统模型设计了最优状态观测器，获得了具有最小方差无偏准则下的状态估计。

附录A

将式(15)左右同时乘以传感器偏差模型量测矩阵Hk+1，可得

(A1)

由式(7)可知

(A2)

联立式(A1)和式(A2)，可得

(A3)

由式(A3)可得出uk的通解为

(A4)

将式(A4)代入式(15)，可得

(A5)

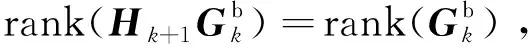
(A6)

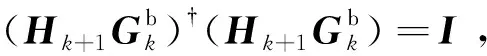
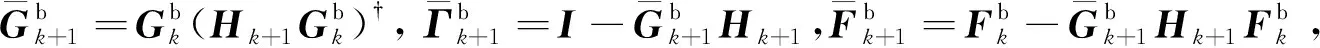
(A7)

证毕。

附录B

(B1)

(B2)

(B3)

(B4)

因此，

(B5)

将式(B5)代入式(B1)～式(B4)中进行化简，可得

(B6)

证毕。

附录C

将最优状态观测器应用于具有未知干扰的随机系统，即将式(23)代入式(22)中，状态估计误差为

xk+1-(zi,k+1+Mi,k+1(Ci,k+1xk+1+ηi,k+1+

(I-Mi,k+1Ci,k+1)(Akxk+Bkμk+ζk+Ekdk)-

Mi,k+1Ci,k+1)ζk-[Li,k+1-(I-Mi,k+1Ci,k+1)·

(I-Mi,k+1Ci,k+1)Ekdk-[Ti,k+1-

(I-Mi,k+1Ci,k+1)]Bkμk

(C1)

当rank(Ci,k+1Ek)=rank(Ek)成立时，Ci,k+1Ek为一列满秩矩阵(因为矩阵Ek作为未知干扰输入矩阵，默认为列满秩矩阵)，则Ci,k+1Ek存在左逆矩阵，即

(Ci,k+1Ek)†=[(Ci,k+1Ek)TCi,k+1Ek]-1(Ci,k+1Ek)T

定义Mi,k+1=Ek(Ci,k+1Ek)+，则有

Mi,k+1Ci,k+1Ek=Ek(Ci,k+1Ek)+Ci,k+1Ek=

Ek[(Ci,k+1Ek)TCi,k+1Ek]-1(Ci,k+1Ek)T·

Ci,k+1Ek=Ek

即公式Ek=Mi,k+1Ci,k+1Ek恒成立。

再定义

(C2)

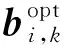
证毕。

附录D

由式(C2)，可得状态估计协方差矩阵为

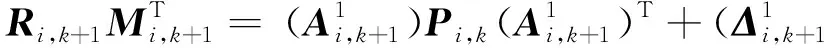
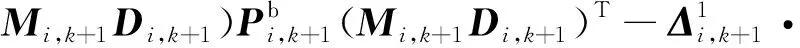
(D1)

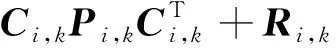
(D2)

令

(D3)

则协方差矩阵为

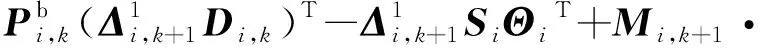
由式(D2)与式(D3)可得

(D4)

此时，状态估计协方差矩阵由式(D5)给出

(D5)

证毕。