考虑分子转动自由度的离散统一气体动理学格式
姚博,张创,郭照立
华中科技大学 煤燃烧国家重点实验室,武汉 430074
多尺度流动在工程应用中广泛存在,例如临近空间飞行器、微机电系统(Micro-Electro-Mechanical System,MEMS)等问题中,同一个计算域内会同时存在连续流、滑移流甚至是自由分子流等不同流域,局部努森数可能相差数个量级[1]。在稀薄流中,基于连续介质假设的Navier-Stokes方程不再成立。常规求解Boltzmann方程的计算格式往往采用算子分裂方法[2-4],存在时间步长小于平均碰撞时间、网格尺寸小于分子平均自由程的限制。而多尺度问题中连续流的存在,使得直接使用这类方法计算整个流场消耗相当巨大。
多尺度流动问题的直观解决方法是将不同求解器耦合起来。在局部努森数较大的计算区间中求解Boltzmann方程,在局部努森数较小的计算区间中求解Navier-Stokes方程[5-6]。但准确划分不同流域、合理地将不同流域耦合起来都很困难。近年来,基于动理学理论发展出的一类渐进收敛(Asymptotic Preserving, AP)格式[7],使得同一个算法处理整个多尺度问题成为可能。其中,Xu等提出的统一气体动理学格式(Unified Gas Kinetic Scheme,UGKS)[8-10]采用有限体积形式,在计算网格界面通量时采用控制方程在时间上的局部积分解,耦合了粒子间的碰撞与迁移过程,能够准确描述连续流到稀薄流流域的流动问题。Guo等提出的离散统一气体动理学格式(Discrete Unified Gas Kinetic Scheme,DUGKS)[11-13]也采用有限体积形式,继承了UGKS的主要优点,但与UGKS也存在明显的不同。在构造界面通量时,DUGKS采用的是沿特征线积分得到的数值解,计算效率更高[14]。
在实际的多尺度流动问题中,气体往往是多原子气体,如空气的最主要成分是氧气和氮气2种双原子气体。氧气和氮气的转动特征温度分别为2.07 K和2.88 K,因此即使在室温下其转动能也能被充分激发出来。而由于振动特征温度具有较高的值(氧气与氮气分别为2 256 K和2 719 K),只有达到较高的温度振动能才会被激发[15-17]。Rykov模型[18]就是考虑了分子平动和转动自由度的动理学方程,能适用于较大范围的双原子气体流动问题研究。近年来,不少工作基于Rykov模型方程研究了双原子气体流动问题[19]。例如Rykov等[20-22]先后计算了双原子气体的正激波结构和微管道内的流动;Liu等[23]构造出了基于Rykov模型方程的统一UGKS,计算的正激波结构、外掠平板等多个算例与直接蒙特卡罗(Direct Simulation Monte Carlo,DSMC)和实验结果吻合良好;Wu等[24]将Rykov模型方程中的弹性碰撞项用Boltzmann碰撞项替换,并采用快速谱方法进行求解。
本文构造出了基于Rykov模型方程的离散统一气体动理学格式,从单原子气体拓展为计算考虑了分子转动自由度的双原子气体,能够有效模拟双原子气体从连续到稀薄的多尺度流动问题。
1 Rykov模型方程
Rykov模型方程考虑了气体分子内部的转动自由度,分别处理分子的弹性碰撞和非弹性碰撞[18]。气体分子的速度分布函数记为f=f(t,x,ξ,η,e),其中t为时间,x为空间坐标,ξ为分子在D维空间中的平动速度,η为分子速度在三维空间中的其他分量,e=M2/(2J)为分子转动能,M为角动量,J为转动惯量。宏观量可以通过分布函数定义为

(1a)
(1b)
(1c)
(1d)
(1e)
(1f)
q=qr+qt
(1g)
式中:c为分子热速度,c=ξ-U;k为玻尔兹曼常数;n为分子数密度;m为分子质量;U为流体速度;Tt和Tr分别为平动和转动温度;ε为分子转动自由度对应的平均能量;qt为与平动自由度对应的热流;qr为转动能量传输产生的热流;ρ为密度。
在不考虑外力项的情形下,Rykov模型方程中气体分子速度分布函数f=f(t,x,ξ,η,e)的演化方程有如下形式:
(2)
式中:右侧两项分别表示非弹性碰撞项和弹性碰撞项。弹性碰撞项保持平动动能守恒,非弹性碰撞项则实现平动和转动二者间能量的转换。νt和νr分别为弹性和非弹性碰撞频率;ft和fr分别为弹性碰撞项和非弹性碰撞项的平衡态:
(3a)
(3b)
(3c)
(3d)
式中:松弛时间τ=μt/pt,μt和pt分别为温度Tt对应的动力黏度和压力;T为平衡态温度;参数Z反映单一转动碰撞中平动碰撞发生的次数;D0为双原子气体的自扩散系数;ω0和ω1用于调整热流qt和qr至合适的松弛值:
(4a)
(4b)
Rykov在文献[18]中将分布函数对转动能e求积,引入2个约化的分布函数,式(2)则转化为2个关于约化后分布函数的方程。在D维问题中,分布函数的演化仅与D维的离散速度ξ有关而与η无关。为进一步消除分布函数对冗余变量的依赖,降低计算消耗,可采用类似的处理方法引入3个约化的分布函数
(5a)
(5b)
(5c)
则宏观量可表示为
(6a)
(6b)
(6c)
(6d)
(6e)
(6f)
q=qr+qt
(6g)
式中:R为气体常数。
分布函数f0、f1和f2的控制方程可对式(2)积分得到
(7a)
(7b)
(7c)

(8a)
(8b)
(8c)
(8d)
(8e)
(8f)
(8g)
(9a)
(9b)
(9c)
控制方程式(7)可以改写为
(10a)
(10b)
(10c)
2 数值格式
本节基于式(10)构建考虑分子转动自由度的离散统一气体动理学格式。首先将其统一为
(11)

(12)
(13)
式中:Fn+1/2(ξ)为穿过网格界面的流量;Δt=tn+1-tn为时间步长;|Vj|和∂Vj分别为控制体Vj的体积和表面积;dS为表面积;r为指向控制体表面外的单位法向量;φj和Ωj为单元上分布函数和碰撞项的平均值:
(14a)
(14b)
(15a)
(15b)
于是式(12)转变为
(16)
由式(11)中碰撞项的守恒性可以得到
(17a)
(17b)
(17c)
(17d)
(17e)
(17f)
q=qr+qt
(17g)
计算界面流量Fn+1/2的关键在于获得界面处原始分布函数fn+1/2。DUGKS采用在半个时间步长s=Δt/2内对式(16)沿特征线积分:
φ(tn+s,xb,ξ)-φ(tn,xb-ξs,ξ)=
(18)

(19a)
(19b)
则式(18)可以写为
(20)
其中:
(xb-xj-ξs)·σj,(xb-ξs)∈Vj
(21)

(22a)
(22b)
(22c)
(22d)
(22e)
(22f)
q=qr+qt
(22g)
通过tn+1/2时刻界面处宏观量可以得到的相应的Rykov分布函数φR,依据式(19)得到原始的分布函数:
(23)
在上述推导中,分子运动速度ξ被认为是连续的。在实际计算中,需要将速度空间离散为速度集ξi(i=1,2,…,N)。离散速度集通常选为Gaussian-Hermite或Newton-Cotes等特定数值积分公式的节点坐标,上述积分需要被替换为数值积分。例如,对于守恒变量有
(24a)
(24b)
(24c)
(24d)
由于在重构界面分布函数时耦合了分子的碰撞和迁移过程,DUGKS具备渐进收敛特性。DUGKS中的时间步长由Courant-Friedrichs-Lewy (CFL)条件确定[11]:
(25)
式中:ζ为CFL数;Δx为最小网格尺寸;ξm为最大离散速度值;Um为最大流动速度。
对于定常流动问题,选取2个相邻时间步中宏观量场的平均变化比α作为计算收敛的判据:
(26)
式中:W∈{ρ,U,T},当α小于给定的参考值时认为计算达到收敛。
Rykov模型方程中参数Z与旋转碰撞数Zrot之间存在如下关系[24]:
(27)
其中,当计算双原子时固定参数d=2。Zrot可采用Landau-Teller-Jeans转动能量松弛模型[25]计算得到,即
(28)

3 数值验证
本节将采用数个双原子气体流动的问题验证基于Rykov模型方程的DUGKS方法的正确性和有效性,包括一维氮激波结构、二维超声速平板绕流、二维超声速圆柱绕流和2个连通方腔中的跨流域流动等问题。
3.1 激波结构
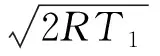
(29a)
(29b)
(29c)
(29d)
式中:Ma为上游马赫数;Ma′为下游马赫数。
计算域选为-25λ1≤x≤25λ1,并采用100个均匀分布的物理网格。速度空间取为-15≤ξ≤15,采用201个均匀分布的Newton-Cotes积分点。x≤0范围内的分布函数初始值为上游参数确定的平衡态分布,x>0范围内的分布函数初始值为下游参数确定的平衡态分布。平动温度Tt和转动温度Tr的初始值与平衡态温度T相等,即Tt1=Tr1=T1和Tt2=Tr2=T2。激波上下游边界处分布函数分别固定为上下游宏观量对应的平衡态分布。计算中CFL数均取为0.95,收敛判据为热流的平均变化比小于10-8,即αq<10-8。
DSMC方法中取ZDSMC=3.5,DUGKS和UGKS当中Z=2.4,根据文献[24]取参数δ=1/1.33,ω0=0.477以及ω1=1.919。分别比较了Ma=1.53、4.0、5.0和7.0 这4种马赫数下的氮激波结构。图1给出不同马赫数下,DUGKS与文献[23]中UGKS和DSMC的氮激波结构计算结果对比。图1中均为归一化后的宏观量,以Q表示宏观量,下标u和d分别表示上游和下游值,归一化后为Q′=(Q-Qu)/(Qd-Qu)。可以看到,DUGKS与UGKS的计算结果在不同马赫数下都吻合良好。二者计算的密度曲线与DSMC的结果吻合良好,温度曲线则在激波上游位置上升得更早一些。产生这一差异的主要原因是DUGKS和UGKS采用的松弛模型只采用了单一的松弛时间,在靠近激波上游的位置将高速分子的能量平均分配给全部分子[12]。

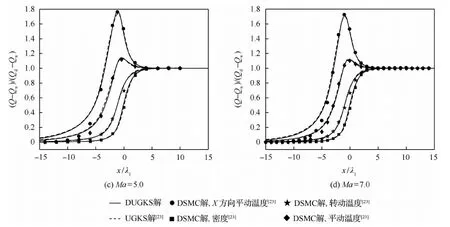
图1 不同马赫数下DUGKS、UGKS和DSMC的氮激波结构计算结果对比Fig.1 Comparison of nitrogen shock structure results of DUGKS, UGKS, and DSMC under different Mach numbers
3.2 超声速平板绕流
飞行器在临近空间飞行中以高超声速飞行时,流场中存在激波-激波、激波-壁面的相互作用,飞行器表面附近会出现高热流和高压强的现象。
本算例取自Tsuboi和Matsumoto[26]的风洞试验run34,Xu等[27]基于多温度模型方程的气体动理学格式,Liu等[23]基于Rykov模型方程的统一气体动理学格式,先后对该问题进行了数值模拟。在run34试验中,喷嘴出口马赫数Ma=4.89,总温T0=670 K,总压p0=983 Pa,喷嘴出口温度Te=116 K,密度ρe=6.15×10-5kg/m3。平板由金属铜制造而成,试验中通过水冷实现恒温290 K。试验气体为氮气,气体常数R=297 J·kg-1·K-1,热度系数ω=0.75。黏性与温度之间关系为
(30)
式中:μ0=1.656×10-5Pa·s,T0=273.5 K。计算中采用硬球分子模型,平均自由程λ与黏性的关系为
(31)
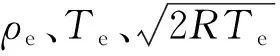
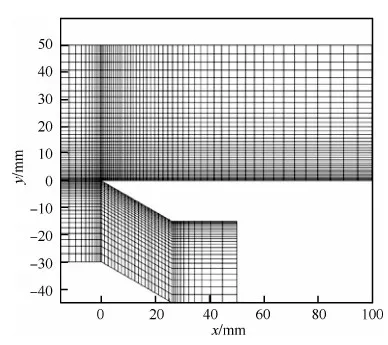
图2 超声速平板绕流计算网格Fig.2 Computational mesh for supersonic flow around flat plate
图3(a)~图3(d)分别为计算得到的密度、平均温度、平动温度以及转动温度云图。可以看到,转动温度Tr升高滞后于平动温度Tt。这一现象可以解释为:高速的双原子气体与壁面碰撞后,宏观动能转换为分子热运动动能,使平动温度升高。经过分子间的相互作用,再传递给转动温度对应的内能。在平板上端x=5 mm和x=20 mm处沿坐标y方向上的温度曲线在图4中给出,计算结果与实验数据、UGKS解总体吻合良好。
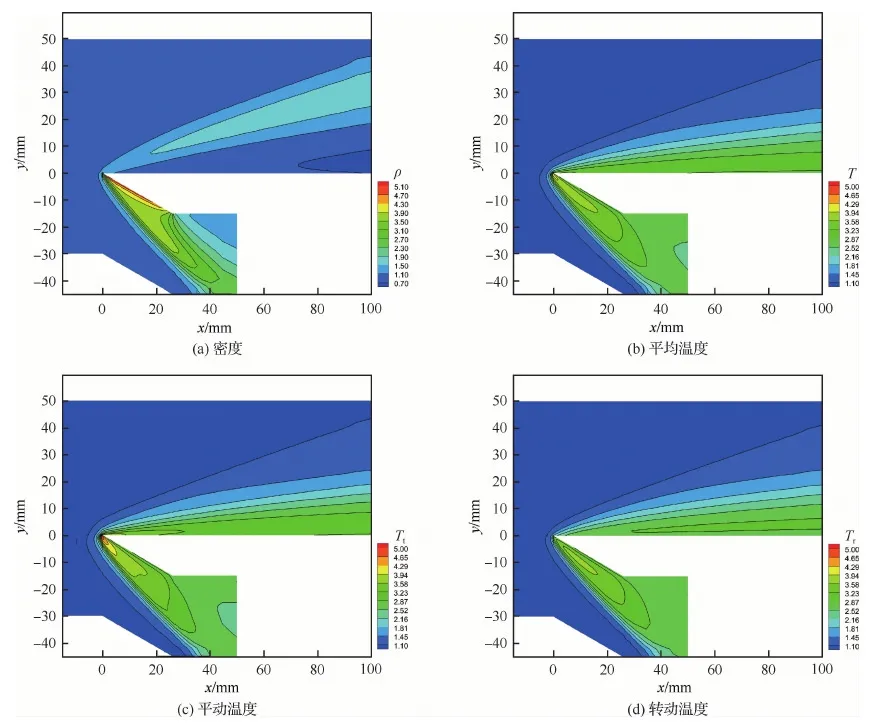
图3 DUGKS计算的平板绕流密度、平均温度、平动温度和转动温度云图Fig.3 Contours of DUGKS results around flat plate for density, equilibrium temperature, translational temperature, and rotational temperature
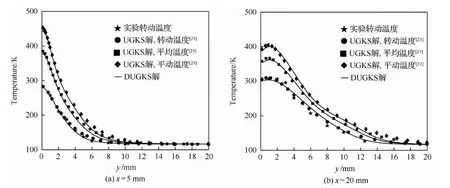
图4 x=5 mm和x=20 mm处沿y方向温度分布曲线对比Fig.4 Temperature plots along y direction at x=5 mm and x=20 mm
3.3 超声速圆柱绕流
本算例进一步测试了氮气的超声速钝体绕流问题,算例来源于文献[23]。来流氮气的速度U∞=1 684.5 m/s,温度T∞=273 K,分子数密度n∞=1.299 44×1021/m3,动力黏度μ∞=1.657 88×10-5Pa·s,取热度系数ω=0.75。圆柱表面为恒定温度Tw=273 K。可计算出,来流氮气马赫数Ma=5.0,努森数Kn=0.1。


图5 超声速圆柱绕流计算网格Fig.5 Computational mesh of supersonic flow around a cylinder
图6(a)~图6(f)分别为DUGKS计算圆柱绕流的密度、x方向速度、y方向速度、平均温度、平动温度以及转动温度云图。图7显示的是在y=0 m处沿x方向的参数曲线。可以发现,DUGKS计算的密度、速度曲线都与UGKS和DSMC结果吻合良好,而DUGKS和UGKS二者的温度曲线比DSMC的计算结果上升地更早一些,这与前面的一维激波结构的研究结论是一致的。
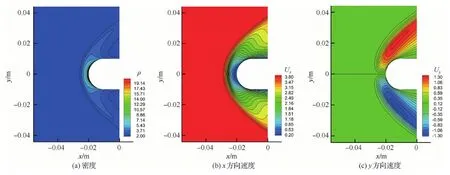
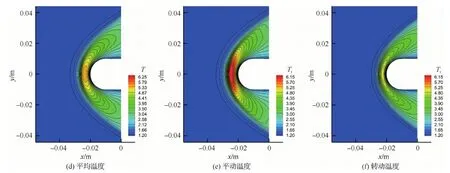
图6 DUGKS计算的超声速圆柱绕流流场云图Fig.6 Contours of supersonic flow around a cylinder of DUGKS results
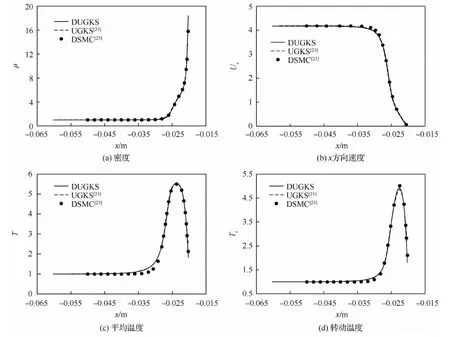
图7 超声速圆柱绕流在y=0 m位置的流场分布Fig.7 Flow distributions along line y=0 m for supersonic flow around a cylinder
3.4 两个连通方腔中的跨流域流动
在太空探索中,火箭燃料罐爆裂或者宇航仓泄漏时,泄漏到太空中的气体会经历从连续流到自由分子流等不同流域的变化。高效地模拟跨流域流动对预测航天器泄漏等实际问题具有指导意义。本算例参照文献[28]构造出了2个方腔中的跨流域流动,如图8所示。方腔及管道中气体为氮气。方腔边长为L=1 m,管道长为L,宽为H=L/8。初始状态下,左、右两个方腔分别维持在不同压力,管道中间处的隔板将两侧气体分开。两侧气体温度均为273 K,左侧压力pL=48.16 Pa,右侧压力pR=0.004 816 Pa。方腔及管道壁面均为恒定温度Tw=273 K。可计算得到,左、右两侧的努森数分别为KnL=0.001和KnR=10,左侧处于连续流域,右侧接近自由分子流域。在t=0 s时刻,移去管道中的隔板,左侧的气体在压力的作用下迅速喷入右侧。

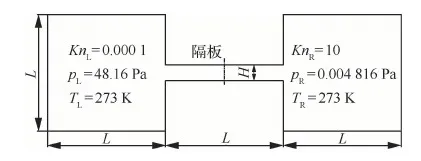
图8 两个连通方腔跨流域流动示意图Fig.8 Schematic diagram of multiscale flow of two connected cavities
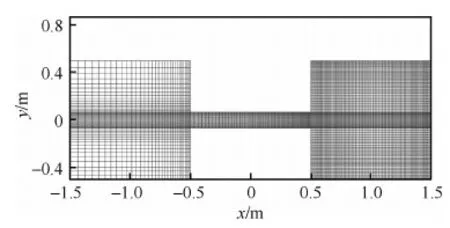
图9 两个连通方腔跨流域流动的计算网格Fig.9 Computational mesh of multiscale flow of two connected cavities
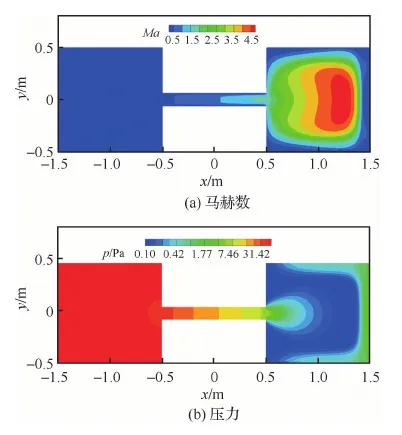
图10 t/tc=1时马赫数及压力分布云图Fig.10 Contours of Mach number and pressure at t/tc=1

图11 t/tc=0.09,0.5,1.0和2.0时刻沿中轴线(y=0 m)温度分布曲线Fig.11 Temperature distributions along line y=0 m at time t/tc=0.09, 0.5, 1.0, and 2.0
4 结 论
基于考虑分子转动自由度的离散统一气体动理学格式,对激波结构、超声速平板绕流以及超声速圆柱绕流等算例进行计算,得到以下结论:
1) 基于Rykov动理学模型方程并采用Landau-Teller-Jeans转动能量松弛模型的离散统一气体动理学格式,可以反映出双原子气体非平衡流动时转动和平动自由度对应的能量转换过程,可用于计算双原子气体的多尺度流动问题。
2) DUGKS计算的结果与UGKS、DSMC的解以及实验值吻合良好。其中,激波结构算例中马赫数范围从1.5变化到7.0,超声速外掠平板以及超声速圆柱绕流分别测试了DUGKS在带有尖端的平板以及钝体中的计算性能,验证了考虑分子转动自由度的离散统一气体动理学格式的准确性及稳定性。
本文仅构造了考虑分子转动自由度的离散统一气体动理学格式并验证了一维及二维算例,同时考虑分子振动自由度并将其应用于实际的复杂三维计算有待进一步研究。

