基于纯追踪模型的算法改进

郭璧玺，杜兴乐，陶小松

（长安大学 汽车学院，陕西 西安 710064）

1 前言

智能汽车研究的重要问题之一就是路径跟踪问题，路径跟踪的实质其实指的是智能汽车平稳且无误差的按着上层已规划决策好的期望路径行驶的能力。郭景华[1]等教授较为全面地总结了目前在路径跟踪控制方面的最新研究成果，对其主要方法有：纯跟踪算法、模糊控制方法、滑模控制方法、模型预测控制算法、PID 控制方法、H 鲁棒方法等。其中，对于纯追踪算法的研究很早之前就已开始，因简单易用而得到广泛应用。纯追踪算法的路径跟踪效果好坏主要取决于前视距离选定。

较大的前视距离可能会使车辆沿着期望路径行走时产生“走捷径”现象，不能很好地跟踪整个路径；较小的前视距离会使可能会使车辆跟踪会产生振荡。本文对于前视距离的调节综合考虑车速以及横向偏差与航向偏差，实现了对前视距离的较好调节，对仿真结果的分析后发现，此方法提高了智能车的路径跟踪效果。

2 二自由度汽车运动学模型

分析中忽略转向系统的影响，直接以前轮转角作为输入；忽略悬架的作用，认为汽车车厢只进行与地面平行的平面运动，即忽略汽车竖直方向的位移，并且忽略汽车的俯仰角以及侧倾角，因此，将汽车简化为线性二自由度的汽车模型[2]。下图为二自由度汽车的运动学模型。

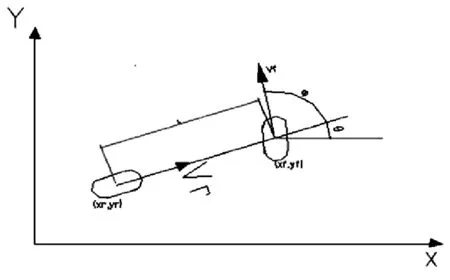
图1 车辆运动学模型

对上述车辆运动学模型进行简单推导后可以得到如下运动学等式：

式中：xr为车辆位置的横坐标，vr为车辆后轴瞬时速度，θ 为车辆的航向角。

式中：yr为车辆位置的横坐标，vr为车辆后轴瞬时速度，θ 为车辆的航向角。

式中：φ 为前轮转角，vr为车辆后轴瞬时速度，θ 为车辆的航向角。

3 纯跟踪算法

纯跟踪算法在智能车辆路径跟踪控制中的应用已有大量的研究，该算法假设车辆从起始点沿着一条圆弧路到达期望的目标位置，根据车辆的阿克曼转向定律很容易就得到前轮转向角的控制量[3]。每执行一个指令周期后，更新后轴坐标以及前视距离，就可以得到实时的前轮转向角控制量。

图2 纯跟踪算法

由上述运动学模型，根据几何知识，容易推导出：

式中：为车辆航向与前视向量之间的夹角，ld 为前视距离，R 为车辆作圆周运动的转向半径。

由阿克曼转向定律可知：

式中：δ 为前轮转角，L 为车辆的，R 为车辆作圆周运动的转向半径。

将公式（4）代入公式（5）之中，可得前轮转角控制量为：

纯跟踪算法研究的重点始终是前视距离的选定[4]，传统纯跟踪算法的前视距离定一般按如下公式确定：

式中，Lamin 是使得车辆稳定跟踪路径的最小前视距离，K 为车速的增益，v 是车辆当前行驶速度，|v|c是一个车辆行驶速度界限值。

4 基于模糊控制器对纯跟踪算法的改进

按照公式（7）确定的前视距离，只考虑了车速对前视距离的影响，这明显是不合理的。当横向误差或者航向误差较小，而车速较高时，由于此时的前视距离过大，会导致下一时刻无人车对路径的跟踪误差大大增加，并且很长时间以后才能将跟踪误差减小。所以，引入模糊控制器对公式（7）中的可调增益K 进行处理，将模糊控制器的输入设为横向偏差以及航向偏差，输出设为前视距离，由此，就可以综合考虑车速，横向偏差以及航向偏差给前视距离带来的影响，得到更合理的前视距离参数。

将横向偏差和航向偏差作为模糊控制器的两个输入[5]，输出设为车速的增益K，模糊语言值为：

（1）横向偏差Ed：{右大，右中，右小，零，左小，左中，左大}={YD,YZ,YX,O,ZX,ZZ,ZD}，根据实验结果，一般将横向偏差的论域确定为[-15m,15m]。

（2）航向偏差Ec：{右大，右中，右小，零，左小，左中，左大}={RB,RM,RS,Z,LS,LM,LB}，规定车体航向偏向期望路径左侧时，航向偏角为正，其论域为[-90°,90°]。

（3）车速的增益K：{很大，大，较大，适中，较小，小，很小}={VB,B,CD,M,CS,S,VS}，根据对实验数据的计算推导，可以确定车速的增益K 一般为[1,4]。

为了简化算法，采用标准的三角形隶属度函数。确定各变量论域以及隶属度函数以后，再确定模糊推理规则。模糊推理规则的制定原则为：横向偏差与航向偏差越大，车速的增益K 就越大，反之则越小。这里共总结了 49 条模糊推理规则，制定了模糊推理规则表，如表 1 所示。

表1 模糊推理规则表

由模糊推理机制得出的速度增益K 是一个模糊子集，需要进行解模糊化，本文采用重心法进行解模糊化操作。

5 MATLAB 仿真及结果分析

5.1 直线路径跟踪仿真

设定车辆初始位置在（0,0）点处，航向偏角为-45°。传统算法与改进算法的跟踪轨迹如图3（a）所示。横向偏差随时间变化曲线如图3（b）所示。可以看出，传统算法的最大横向偏差为1.44m，平均误差为0.53m，并且误差处于逐渐减小的振荡状态。改进算法的最大横向偏差为0.12m，平均偏差为0.013m，并且车辆在第3.5s 进入期望路径。

图3 直线路径跟踪比较图

5.2 定曲率路径跟踪仿真

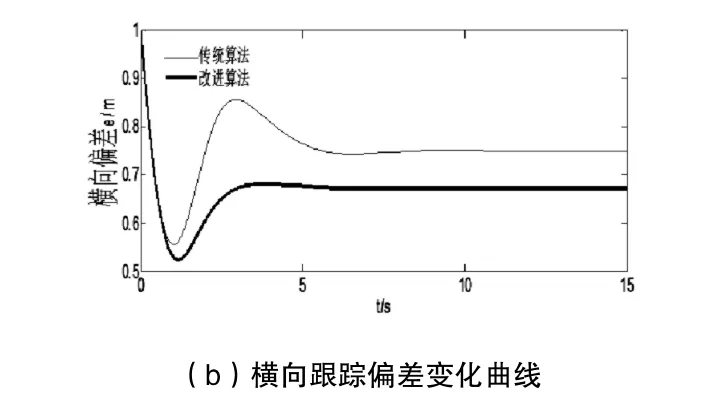
图4 定曲率路径跟踪比较图

设定车辆初始位置在（0,0）点处，航向偏角为-90°。传统算法与改进算法的跟踪轨迹如图4（a）所示。横向偏差随时间变化曲线如图4（b）所示。可以看出，传统算法的最大横向偏差为1m，平均偏差为0.75m，并且车辆在第6s 进入期望路径。改进算法的最大横向偏差为1m，平均偏差为0.65m，并且车辆在第4s 进入期望路径。

6 结论

以上将横向偏差与航向偏角作为输入，应用模糊算法对纯追踪算法公式（7）中的可调增益K 进行调节，从而得到更合理的前视距离，减小了跟踪误差，缩短了调节时间。对传统算法和改进算法在两种道路形状下仿真的跟踪效果进行分析比较，可看出改进后的纯跟踪算法能更好地跟踪路径，最大跟踪误差和全程平均误差都明显减小。并且，在跟踪直线路径与定曲率路径时，改进算法的调节时间都大大缩减。可见，改进后的算法能够适应实际车辆行驶过程中的动态要求，有效地提高了路径的跟踪效果。