柯西不等式三用

施建昌 陈文珍

(1.浙江省绍兴市柯桥区教师发展中心 312030;2.浙江省绍兴市锡麟中学 312069)

柯西不等式不仅形式优美而且具有重要的应用价值，许多不等式问题通过柯西不等式化解往往事半功倍，使人耳目一新．下面就柯西不等式的三个重要应用进行例析.

一、变形凑数用柯西

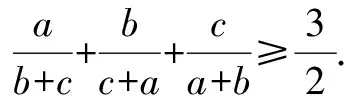
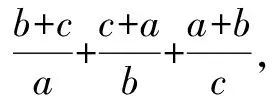
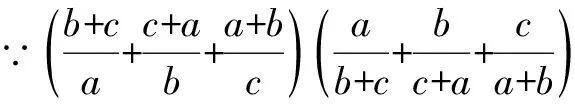
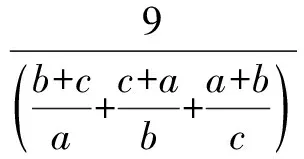
点评直接应用柯西不等式化解的问题一般易于破解，有些问题不易直接进行化解，则需要进行必要的凑、补等手段才能达到，因此要注意对于已知的式子进行必要的变形，以利于柯西不等式的应用．

二、二用柯西传递证

例2已知正数a,b,c满足a+b+c=1，

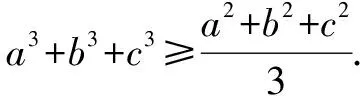
分析这个问题首选要进行变形运用柯西不等式，将不等式两边同乘以3进行转化，但一步很难达到目标，则时不妨再用柯西不等式进行处理，问题便可迎刃而解．

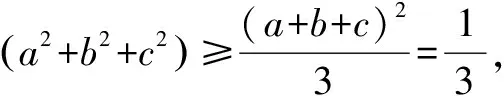
点评对于柯西不等式的应用，有时一步不能完成，要注意是否继续符合或变形后符合柯西不等式的情况，如果符合则要继续应用柯西不等式进行化解．

三、减少变量用柯西

例3已知实数a,b,c,d满足a+b+c+d=3，a2+2b2+3c2+6d2=5，试求a的范围.

分析这是一个涉及到四个变量的柯西不等式问题，对于三维柯西不等式的应用还是有公式可扩展的，但这个涉及到四元的柯西不等式直接求解难度较大，需要通过恒等变形减少变量以达到目标．

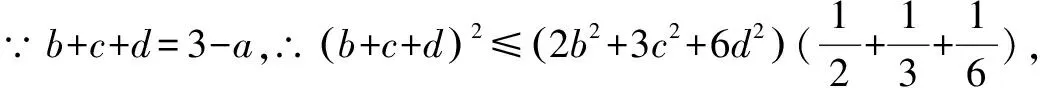
点评减少变量个数运用柯西不等式是一种变形技巧，一般理解是四元的就用四元的柯西不等式，然而因为要求其中的一个变量的范围，因此要注意减少一个变量运用柯西不等式，通过柯西不等式转化为所求变量的一元不等式进行处理．

柯西不等式作为选修模块的一个重要内容，在不等式问题的处理中占有重要地位，在学习其必要性质的前提下，理解和掌握好以上三类柯西不等式的重要应用十分必要．