分组巧解题
黄旭军
老师走进教室,“唰唰唰”地在黑板上写下“百僧吃百馒头”,转身说道:“今天我要教给大家的绝招是分组法。”
“什么是分组法?”同学们议论纷纷。老师说:“在解决问题时,有些数量是可以按照一定规律来分组计算的。只要看出哪些数量可以归到同一组,并计算出总数量中包含多少个这样的组,就能计算出每种物品的数量各是多少了。这就是分组法。在做某些题时,它比列方程要快捷得多。”
例1 100个和尚吃100个馒头。大和尚一个人吃3个,小和尚3个人吃1个,大、小和尚各有多少人?
观察开始
已知和尚、馒头的总数量,而“大和尚一个人吃3个,小和尚3个人吃1个”相当于“每个大和尚吃3个馒头,每个小和尚吃1/3个馒头”。
常规思路
我们可以通过列方程来解决问题。
另辟蹊径
若没学方程,怎么办呢?我们可以用分组法解决问题。
根据“大和尚一个人吃3个,小和尚3个人吃1个”,可以把3个小和尚与1个大和尚归为一个吃馒头小组,也就是每组4个和尚(1大3小)吃4个馒头。
100÷(3+1)=25(组)。每组1个大和尚,所以有25个大和尚;每组3个小和尚,所以有25×3=75(个)小和尚。
例2 现有1元、5元、10元人民币共20张,共130元,其中1元、5元的数量相等,三种人民币各有多少张?
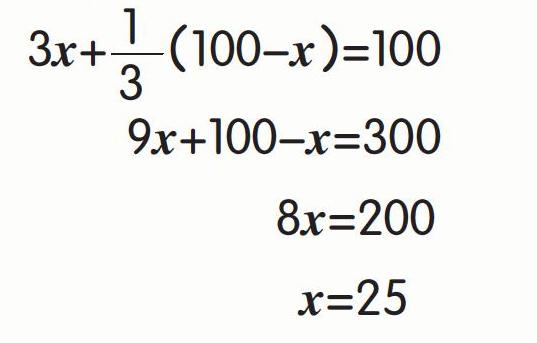
?
观察开始
未知量有3个,已知人民币总数量和总金额,且1元和5元的数量相等。
常规思路
设1元有x张,则5元也有x张,10元有(20-2x)张。
10(20-2x)+5x+1x=130
200-20x+6x=130
14x=70
x=5
所以,1元有5张,5元有5张,10元有20-2x=10(张)。
另辟蹊径
分组法求解更简便。
由于1元、5元的数量相等,把1张1元和1张5元合成一组,每组是2张,共6元。也就是说,一个6元对应2张,相当于每张3元。
这样一来,题目就变成了“3元和10元共20张,共130元”。而3元和10元合成组,刚好13元一组,130÷13=10,正好10组,所以3元有10张,10元也有10张。
3元是1元和5元分组得到的,由此可得1元有5张,5元有5张。
列式为:
(5+1)÷2=3(元)
130÷(10+3)=10(组)
10÷2=5(张)
所以,1元有5张,5元有5张,10元有10张。
训练一二一
蜘蛛、蝴蝶共有506条腿,蜘蛛的数量是蝴蝶的2倍。已知蜘蛛有8条腿,蝴蝶有6条腿,蜘蛛、蝴蝶各有多少只?(答案見下期)

