改进广义灰色关联故障树的危化品LSSC可靠性诊断*

陈 香，龚本刚 ，蒋 培

(1.安徽机电职业技术学院 经济与贸易学院，安徽 芜湖241002； 2. 安徽工程大学 管理工程学院，安徽 芜湖 241000)

0 引言

近年来，随着石化行业快速发展，危化品物流业务外包增多，安全事故频繁发生。如： 2017年张石“5·23”危化品运输爆炸事故等暴露出我国危化品物流运作管理存在诸多问题。危化品物流服务供应链(LSSC)是危化品物流集成化必然产物，危化品LSSC可靠性作为危化品供应链可靠性重要组成部分，是危化品供应链稳定运作的前提和基础，由此引起了人们对危化品LSSC可靠性问题高度关注[1-2]。危化品LSSC可靠运作需要强调链上成员企业能力分工协调，链上任一成员出现问题，都会波及其他成员无法可靠履行客户需求。因此，研究并构建危化品LSSC可靠性失效诊断模型，查找关键事故因素是预防并减少危化品事故发生，提高危化品供应链系统稳定运作的重要保障。李建民等[3]研究并预测海上危化品运输系统的安全性；Kan等[4]运用混合整数规划模型和启发式解决方案对危化品运输路线和时间安排进行研究；Di Fazio等[5]引用欧洲全球导航卫星系统对危化品运输可靠性进行连续定位、控制和监控；王振全[6]对城市危化品物流配送网络可靠性进行研究；宋维花[7]对危化品国际物流运输动态风险和可靠性进行研究；任竞舟等[8]提出基于物元分析的危化品储存安全评价方法；Liu Xuanya等[9]提出基于Bow-Tie模型的危险化学品储存区动态风险评估方法。以上这些研究主要集中在影响危化品供应链运行的某物流功能环节上，如：危化品运输、仓储、配送等，但从供应链集成角度对危化品LSSC系统可靠性优化较少涉及。本文在充分考虑影响危化品LSSC系统可靠运行各种事故因素基础上，对系统失效原因进行全面诊断，快速查找出关键事故因素，给出相应改进措施。

本文将故障树分析法(FTA)和改进广义灰色关联相结合，对危化品LSSC系统进行可靠性诊断，特点是改善FTA中系统故障特征与内部特征之间的弱相关性[10]。下文提到的改进广义灰色关联主要是引入文献[11]离差最大化分配系数计算法。首先构建危化品LSSC系统失效故障树；然后运用灰色关联技术对以最小割集构造的标准故障模式向量和底事件概率重要度组成的待检模式向量进行相关性分析，得到所有失效故障模式可能性排序，确定系统薄弱环节和关键事故因素，起到快速诊断效果，为危化品LSSC风险等级控制和分级防范措施制定提供参考和借鉴。

1 危化品LSSC可靠性诊断的改进广义灰色关联故障树模型

1.1 危化品LSSC系统运营模型

危化品易燃易爆， 是典型的“低概率重后果”，一旦事故发生将会对生命财产和自然环境造成极大危害[12]。危化品LSSC作为一类特殊产品服务供应链，是以危化品物流服务集成商为核心，从功能型服务分包商直至最终客户的供应链结构模式[9，13]。现实中LSSC网链状较为常见，节点运作容易受多个上下游节点企业影响，导致其稳定性较差。危化品LSSC系统运营过程中，政府的宏观监管、应急管理能力，上下游企业应急处理能力、信息反馈及时性，集成商的协调处理能力等对危化品LSSC稳定运行至关重要。本文在参照危化品LSSC内涵基础上，构建如图1所示的危化品LSSC运营模型，模型主要参与实体是政府、危化品服务分包商群、集成商以及目标客户群。在政府宏观监管下，依托政府监管服务平台和危化品综合信息共享平台，危化品服务集成商通过对链上成员实施有效管理，从接受客户需求开始，合理组织分包商，形成一个严格的闭环危化品物流运作系统。

图1 危化品LSSC运营模型Fig.1 Operation model of hazardous chemicals LSSC

1.2 危化品LSSC可靠性诊断模型构建

危化品LSSC可靠性是指在规定约束条件下，危化品物流服务集成商能够准确履行所承诺客户服务能力的一种相对评估[1，5]。本文将FTA与改进广义灰色关联模型融合构建危化品LSSC可靠性诊断模型，具体步骤如下。

1.2.1 确定待检验模式向量和特征矩阵

在FTA中，最小割集代表系统失效故障模式，假设最小割集之间相互独立，则系统最小割集结构函数和顶事件失效概率[14]分别见式(1)和式(2)。实际工作中，最小割集对顶事件发生贡献程度不一样，本文选择概率重要度作为待检验模式向量[11，14]，见式(3)。

(1)

(2)

(3)

式中：pUk代表第K个最小割集Uk发生的概率。根据式(3)所求m个最小割集概率重要度组成1组待检验模式向量，如式(4)所示：

(4)

设特征矩阵为X，其中第i行向量Xi代表每个割集中基本事件组合，且X中元素取值规定只有0和非0这2种[11]，n为故障树基本事件个数，m为最小割集数。即：

(5)

1.2.2 绝对和相对灰色关联度计算

1)绝对灰色关联度计算

绝对灰色关联度反映特征矩阵和待检验模式向量之间纵向差异，引入FTA后可理解为故障模式表征的特征矩阵与底事件概率重要度组成的待检验模式向量之间纵向差异。假设Xi=(xi(1),xi(2),…xi(n))为系统内部因素特征序列，Ii为系统总特征待检测序列，则绝对灰色关联度αoi[11，15]计算如式(6)所示：

(6)

式中：|so|为待检测序列波动幅值和；|si|为特征矩阵内部因素所组成的波动幅值和；|si-so|为待检测序列与特征序列对应各因素波动幅值的差值和；i=1,2,…,m。

2)相对灰色关联度计算

相对灰色关联度可反映总特征序列与各分序列之间的纵向变化差异，引入FTA后可综合反映特征矩阵内每行值变化对待检验模式向量内各因素值变化的影响程度。设相对灰色关联度初始值待检测序列和特征矩阵分别为Ii′和Xi′，Xi′为Xi零像化处理[11]，如式(7)所示。

(7)

式中：i=1,2,…,m;j=1,2,…,n，则相对灰色关联度βoi[11，15]计算如式(8)所示。

(8)

1.2.3 计算广义灰色关联度系数

广义灰色关联度ρoi实质是2序列曲线之间所夹面积的绝对值，从整体上去度量2序列曲线相似性，采用离差最大化分配系数法定义，如式(9)所示[11，15]。

(9)

式中：Bαi和Bβi分别表示绝对和相对灰色关联度的总离差；θ为离差最大化分配系数。

2 应用分析

本文以集成商主导的危化品LSSC为研究对象，运用改进广义灰色关联故障树对危化品LSSC进行失效诊断，结果验证该算法在实际应用中具有切实可行性。

2.1 危化品LSSC可靠性诊断故障树编制

假设某地区高危行业危化品LSSC由1个物流集成商，1个化工制造商以及2个危化品分包商(运输与配送、仓储)所组成。政府负责政策监管、应急救援等服务；集成商负责组织协调；分包商负责功能业务运作。本文将面向终端客户为化工制造商的危化品LSSC服务能力失效作为顶事件，结合该地区危化品专家知识, 在调查危化品物流服务系统日常运作发生风险概率较高事件等基础上得出系统失效风险的主要事故因素。政治、自然、社会、经济等外因发生概率小，故不予考虑，由图1可知，危化品物流集成商、分包商及政府中任何一方失效都可导致顶事件发生，故采用逻辑或连接，并根据逻辑关系从中间事件分析至基本事件，构建危化品LSSC系统失效故障树(见图2)，其中T为顶事件，E为中间事件，u为未开展事件，x为基本事件。

图2 危化品LSSC系统失效故障树Fig.2 Fault tree of hazardous chemicals LSSC system failure

图2中基本事件涵义分别为：集成信息共享不充分(x1)；监控人员失误(x2)；监控设备故障(x3)；危化品分包商选择不当(x4)；任务分配不合理(x5)；配送不准确(x6)；配送质量问题(x7)；驾驶员技术操作有误(x8)；驾驶员应急响应不及时(x9)；运输车辆资质选择不当(x10)；交通布局不合理(x11)；储存环境控制不当(x12)；危化品储存施设备老化(x13)；仓储管理人员违规操作(x14)；仓储内部信息监控有误(x15)；职能部门分工不明确(x16)；企业教育与培训引导不当(x17)；应急响应不及时(x18)；政府违规审查危化品企业(x19)；督促检查不及时(x20)。

2.2 改进灰色关联故障树的危化品LSSC可靠性诊断模型

2.2.1 故障树基本信息与待检验模式向量确定

危化品LSSC运行环境复杂，涉及众多利益实体，基本事件发生具有随机性、不确定性。因此本文在没有充分统计数据资料情况下，采用专家经验、事故调查法，并结合模糊数学等相关理论对基本事件进行概率估算，分别为：P1=0.016；P2=0.025；P3=0.026；P4=0.012；P5=0.015；P6=0.018；P7=0.014；P8=0.048；P9=0.045；P10=0.040；P11=0.046；P12=0.043；P13=0.038；P14=0.042；P15=0.047；P16=0.034；P17=0.028；P18=0.030；P19=0.036；P20=0.020。

假设FTA最小割集分别为U1,U2,…,Uk，采用下行法求解最小割集[14]，经简化吸收后有14个： {x1}，{x2,x3}，{x4}，{x5}，{x6,x7}，{x8}，{x9}，{x10,x11}，{x12}，{x13}，{x14,x15}，{x16,x17}，{x18}，{x19,x20}，根据式(1)和式(2)计算顶事件概率，如式(10)所示。

P(T)=x1+x2x3+x4+x5+x6x7+x8+x9+x10x11+
x12+x13+x14x15+x16x17+x18+x19x20

(10)

将基本事件概率代入式(10)可得：算例中危化品LSSC系统失效概率P(T)=22.7% ，需立即进行可靠性诊断，其中政府、集成商、运输与配送商、仓储商失效概率分别为：

P(E2)=3.2%；P(E11)=4.3%；P(E12)=9.3%；P(E13)=8.1% 。根据式(2)和式(3)可得最小割集的底事件组合概率重要度，即系统待检验模式向量，如表1所示。

表1 各底事件组合概率重要度IiTable 1 Combination probability importance Ii of each bottom event

2.2.2 绝对和相对灰色关联度计算

1)绝对灰色关联度计算

以待检验模式向量表示系统总特征矩阵，首先根据式 (5)可得出分序列特征矩阵X(见式 (11))，然后根据式 (6) 计算得出绝对关联系数，如表2所示。

2)相对灰色关联度计算

2.2.3 广义灰色关联度计算

根据式(9)计算广义灰色关联度系数ρoi见表5所示。

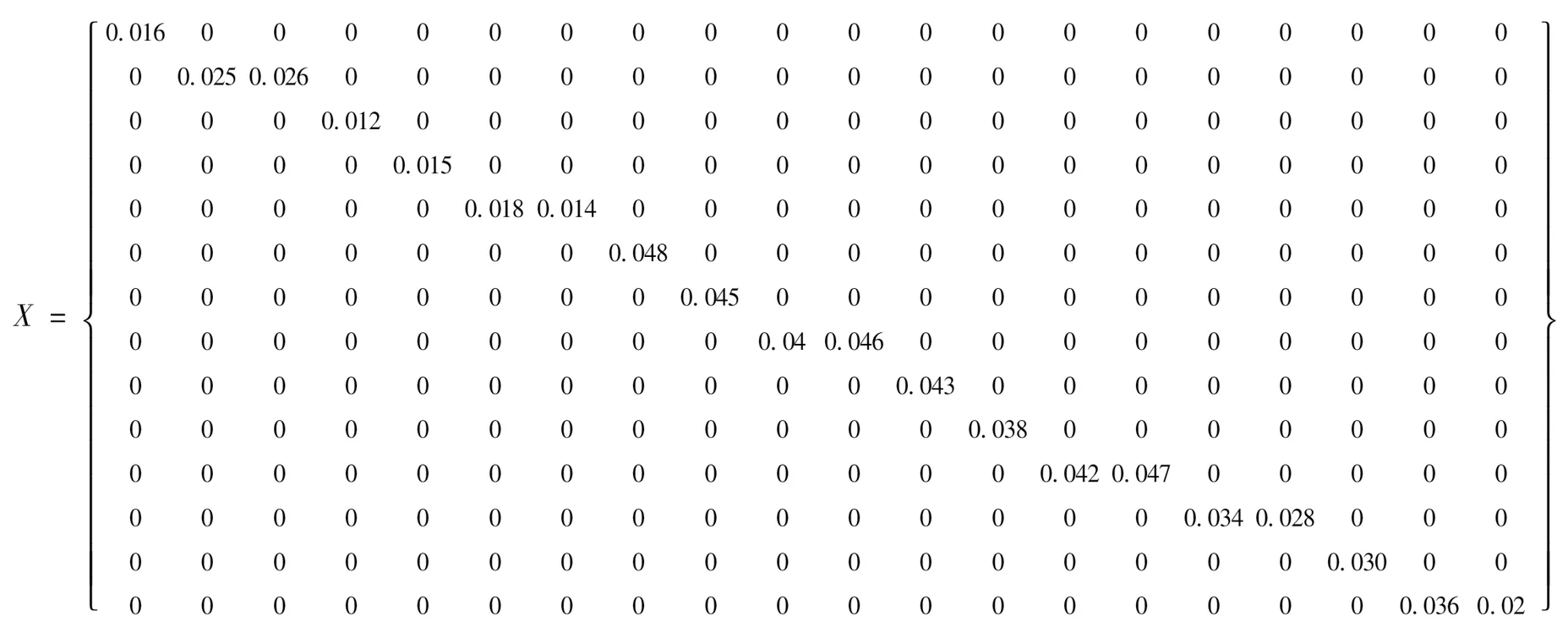
0.016000000000000000000000.0250.026000000000000000000000.012000000000000000000000.015000000000000000000000.0180.014000000000000000000000.048000000000000000000000.045000000000000000000000.040.046000000000000000000000.043000000000000000000000.038000000000000000000000.0420.047000000000000000000000.0340.028000000000000000000000.030000000000000000000000.0360.02

(11)

表2 绝对灰色关联度αoiTable 2 Absolute grey correlation αoi

表3 待检验模式向量Table 3 Pattern vector to be tested

表4 相对关联度βoiTable 4 Relative correlation βoi

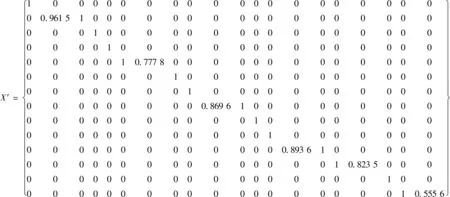
(12)

表5 广义灰色关联度ρoi计算表Table 5 Calculation table of generalized grey correlation ρoi

通过上述计算方法得到算例中导致危化品LSSC系统失效14种故障模式的广义关联度系数ρoi排序为：r2>r11>r12>r5>r8>r14>r7=r9>r10>r6>r1>r4>r3>r13。参考20/80原则，可选取{r2,r11,r12}3个作为危化品LSSC系统执行失效关键故障模式，对应基本事件组合为：{x2,x3}{x14,x15}{x16,x17}，决策者应重点关注该组合对应的关键故障因素，其余故障模式关联值域在[0,0.5]内变化不大，均应时刻保持关注。根据上述计算危化品LSSC系统及链上成员失效概率，参考文献[16]可知算例中危化品LSSC系统执行失效等级概率为5，处于高风险区，需要立即检查。而集成商、分包商失效概率等级为4，处于中高风险区，因此可确定为系统关键薄弱环节。

综上所述，为了预防并减少危化品LSSC系统运作事故发生，集成商应该高度重视监控人员和设备问题；仓储商应多关注仓管人员违规操作、内部信息监控误差等；政府应加强监督，明确职能部门职责分工，加强危化品企业相关安全教育与培训引导，提高危化品企业和相关从业人员的安全意识。

3 结论

1) 将基于离差最大化分配系数的改进广义灰色关联法与FTA结合运用到集成商主导的危化品LSSC系统可靠性诊断中，该方法可综合反映出标准故障模式与待检验模式向量二者的相关性，使得诊断结果更加准确。

2)诊断结果有助于集成商快速识别危化品LSSC系统关键事故因素，起到快速诊断作用；有助于政府及时进行职能评估，根据诊断结果加强监管。

3)本文研究重点是危化品LSSC系统可靠性诊断与验证，未来可对危化品事故应急处理能力、应急响应时间等动态因素对危化品LSSC系统可靠性影响进行探讨，为危化品物流动态化、科学化监管进一步提供参考。