考虑剪切接触与碎屑充填的裂隙渗流模型与数值分析

潘东东，李术才，许振浩，杜毓超，施雪松，高斌，王文扬

(山东大学岩土与结构工程研究中心，山东济南，250061)

伴随着地下能源的开采，受施工扰动影响，岩体裂隙扩展贯通，极易形成导水通道诱发涌水事故，甚至造成突水灾害[1-2]。地下工程中的天然岩体通常由不同尺度的岩石基体和裂缝组成，岩石基质的渗透性与节理裂隙相比基本可以忽略，因此，岩石的水力特性主要由裂隙控制，揭示流体在裂隙中的流动规律具有重要意义。天然裂隙表面结构粗糙，基于理想裂隙(如表面平行、光滑)模型假设计算的流量通常高于实际流量，这种计算偏差给工程应用带来不便。为此，国内外学者开展了大量研究[3]，提出了一系列基于立方定律的修正公式，在一定程度上揭示了裂隙表面粗糙度对渗流的影响规律，但限于当时试验条件与计算机性能，提出的修正公式仍然具有很大的局限性。实际上，裂隙岩体渗流问题不仅与表面粗糙度有关，而且与法向应力、裂隙开度、接触面积、剪切位移以及水力梯度等因素相关[4]。近年来，很多学者致力于通过室内试验的手段研究裂隙渗流特性。速宝玉等[5]通过试验研究，针对仿天然裂隙提出了节理面粗糙度系数修正法，建立了裂隙表面凹凸程度与粗糙度修正系数的关系，为裂隙渗流分析提供了理论基础。熊祥斌等[6]通过设计多组剪切试验研究了单裂隙在不同接触面积以及不同接触分布状态下的渗流规律，并对试验结果进行了数值验证。王刚等[7]通过开展节理面剪切-渗流试验，忽略剪切过程中岩石碎屑影响及节理面凸起的咬断效应，建立了考虑分形特征的裂隙渗流计算模型。但是，室内试验可视性较弱，密封技术作为决定裂隙渗流试验成败的关键技术导致试验代价较高，难以开展重复性试验，因此，人们在裂隙渗流理论模型以及数值计算方面同样开展了大量研究。夏才初等[8]采用自行编制的裂隙空间形貌计算软件，建立了不同接触状态下的节理渗流经验公式，具有广阔的应用前景；朱红光等[9]基于立方定律在二维空间内建立了非线性流动模型，刻画了流体受裂隙粗糙影响下的非线性行为；肖维民等[10]通过建立粗糙节理空腔模型对不同渗流控制方程进行了深入研究，研究结果证实了Reynolds 方程在描述复杂裂隙渗流方面的可行性。李博等[11]根据单节理面的剪切渗流试验结果揭示了裂隙透水系数以及流线的变化规律，并且基于Reynolds方程对试验结果进行了验证。综上所述，裂隙渗流研究目前主要利用模型试验与数值计算2种方法，但由于实验量测以及数值方法的差异，虽然取得了一系列进展，但也面临着诸多问题，主要体现在以下几个方面：

1) 对于裂隙粗糙度的分析，通常采用激光扫描等非接触手段获取裂隙表面信息，并计算其分形维数用于后期计算研究。此类方法可以真实刻画裂隙表面，但随机性较大，可控程度低，定量描述粗糙度的影响需要增加一定的工作量。

2) 在试验研究方面，目前人们主要集中于法向应力作用下裂隙渗流规律的研究，对于剪切作用下裂隙渗流规律的研究仍然有待深入探讨。在模型尺寸方面，无论是室内试验还是数值计算模型采用的裂隙尺度较小，主要为厘米级，与工程尺度的岩体裂隙(米级)差别较大。为此，满轲等[12]开展了大尺度单裂隙渗流试验研究，通过自主研发的应力-渗流耦合试验台架对宽大裂隙的渗透系数进行了研究，但限于模型试验成本，系统研究大尺度裂隙的渗流规律仍然存在较大难度。

鉴于目前研究存在的问题，本文作者通过数值计算方法，利用随机粗糙面功率谱理论建立粗糙裂隙表面模型，模型大小充分考虑实际工程揭露裂隙尺寸，该方法通过考虑分形维数与裂隙起伏标准差可以生成任意粗糙度的裂隙表面。针对具有初始裂隙宽度的裂隙渗流问题，考虑结构面剪切碎屑对裂隙空腔的充填效应，定量化研究剪切过程接触面积变化对裂隙渗流规律的影响，以便得到更加符合工程实际的裂隙剪切渗流模型。

1 裂隙粗糙表面模型生成方法

建立裂隙表面模型是研究裂隙渗流的基础，在建立裂隙表面模型方面，谢和平[13]进行了大量的研究，近些年，随着非接触测量技术的发展，利用激光测试仪对真实裂隙表面进行数据采集，重构裂隙表面建立三维模型进行后期渗流计算求解应用也越广泛。一般而言，随着待研究裂隙尺寸的增大，试样采集成本以及裂隙表面模型的生成难度都随之增加。此外，通过直接扫描岩石表面的方法较难获取不同粗糙度系列样本，因此，采用恰当的数值计算方法快速实现裂隙表面模型的建立尤为重要[14]。

通常天然裂隙是具有分形特征的粗糙表面，在三维分形理论生成裂隙粗糙表面方面，目前主要方法有W-M 函数法，中点位移法、泊松跳跃法、逐次随机增加法、小波变化法以及带限噪声累积法等[15]。该研究利用功率谱密度，采用线性滤波的方法来模拟生成裂隙随机粗糙面[16]。其基本思想是在频域用功率谱对其进行滤波，再进行逆傅里叶变换得到高低起伏的粗糙面，以此得到随机粗糙裂隙表面模型。

若在二维平面内产生随机粗糙面，则x和y方向上的长度分别取值为Lx和Ly，在该研究中裂隙初始模型长×宽为1 280 mm×1 280 mm，将2个方向上的长度进行等距离离散，离散点数分别取值为M和N，相邻两点间的距离分别为Δx和Δy，则Lx≈M·Δx，Ly≈N·Δy。随机曲面上任一点(xm=mΔx,yn=nΔy)(m=-M/2+1,…,M/2;n=-N/2+1,…,N/2)处的起伏高度为[16]

式中：F(kmk,knk)=2π[LxLyS(kmk,knk)]1/2·

S(kx,ky)为二维随机粗糙面的功率谱密度；kmk=2πmk/Lx；knk=2πnk/Ly；N(0,1)为服从均值为0、方差为1的正态分布。另一方面，为了保证f(xm,yn)取值为实数，则要求傅里叶系数的相位满足：F(kmk,knk)=F*(-kmk, -knk)，F(kmk, -knk)=F*(-kmk,knk)。在 具 体计算过程中，通常利用二维逆傅里叶变换实现，其中，二维高斯粗糙面对应的功率谱为

利用上述基本理论编制计算程序可以方便、快捷地生成不同粗糙度的裂隙模型，参考前人研究分别设置6种分形维数研究裂隙表面粗糙度对渗流规律的影响[17]，在该研究中，分形维数分别取2.1，2.2，2.3，2.4，2.5 和2.6，生成的裂隙表面模型如图1所示(在高度方向放大3倍)，图中f为裂隙面的起伏高度。

2 裂隙剪切过程接触分布状态分析

裂隙岩体长期赋存于地下环境中，其中的节理裂隙受地下水侵蚀作用以及水化学作用明显，裂隙面两侧岩石强度低于岩体内部岩石强度，若此时发生剪切作用，则裂隙剪胀作用并不明显，裂隙面上岩体凸起被直接剪断、磨蚀，裂隙接触面积逐渐增大，如图2所示。基于以上论述，该研究在构建裂隙面剪切接触模型时，提出以下基本假设：1)岩体裂隙存在初始隙宽，分别设定为0.1Δ，0.15Δ及0.2Δ(其中Δ为在裂隙面生成过程的最大起伏高度)；2)上下裂隙面在剪切错动过程中，两侧凸起直接剪断，接触即剪断，并以接触面的中间位置作为下一步剪切的初始状态。

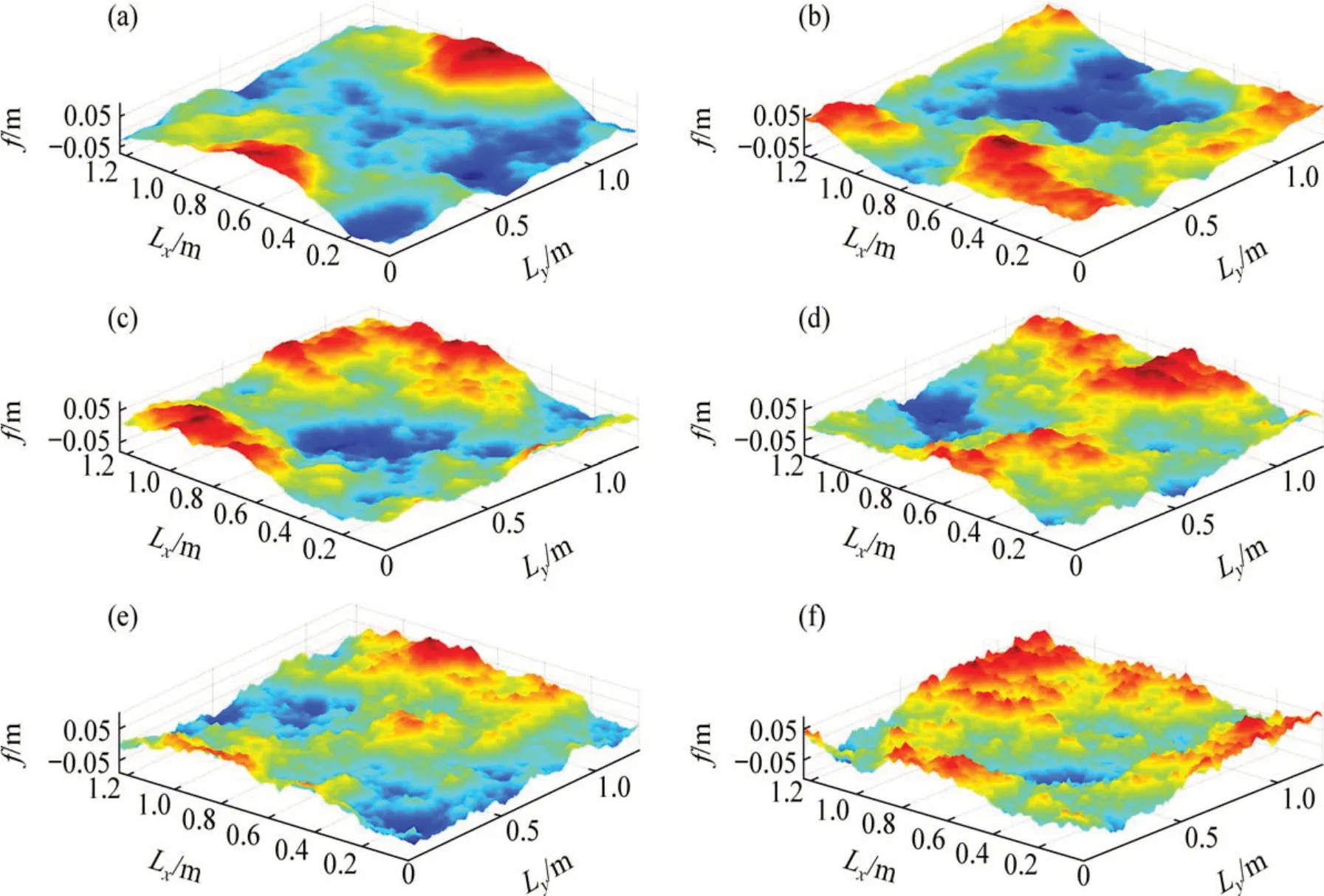
图1 不同粗糙度随机裂隙面Fig.1 Random crack surface of different roughness

图2 裂隙剪切过程接触区域变化示意图Fig.2 Schematic diagram of contact area of fracture shear process

通常天然裂隙隙宽与过流断面尺寸存在数量级上的差别，一般差别为2～3个数量级，直接建立真实三维模型给后期网格划分以及流体计算带来较大困难，甚至难以实现[11]。综合考虑计算能力与实际计算效果，并充分刻画隙宽变化以及剪切过程接触面积的改变，编制相应的计算程序建立了准三维单裂隙渗流计算模型。主要实现步骤为：利用第1节生成的分形裂隙表面模型，计算在一定初始裂隙开度条件下对应不同剪切位移孔隙体积的变化。在垂直剪切方向上的投影即为接触面积的变化特征，则第m次剪切位移过程孔隙体积可以表示为

式中：b(x,y)为裂隙剪切过程节理隙宽分布函数；Ai为上、下裂隙面局部表面面积；bi为局部等效隙宽；N为离散网格数量。

通常岩体裂隙发生剪切错位之后，接触区域出现局部闭合，但尚未完全闭合，仍然具有一定的过流能力。在此研究中，假定闭合区域隙宽为裂隙面的最小隙宽。最后建立离散格式下的二维裂隙模型，将描述隙宽变化的参数代入该模型，赋予每一单元节点以实际隙宽，并采用插值函数对粗糙节理隙宽分布进行处理，得到对应节理面的三维隙宽，如表1所示，以J-1裂隙模型为例描述剪切过程隙宽参数变化。

表1 剪切过程随机隙宽分布统计表Table 1 Statistical table of random gap width distribution of shear process

3 考虑剪切接触与碎屑充填的裂隙渗流模型数值求解

3.1 剪切碎屑影响下的裂隙渗流计算

天然裂隙岩体中的裂隙并非完全贯通，除局部存在接触闭合区域外，通常充填泥沙、岩体碎屑等介质，以往研究通常不考虑裂隙剪切过程岩石碎屑对渗流的影响，这与工程实际问题存在偏差。在此，基于速宝玉等[18]提出的充填裂隙渗透系数计算方法进行研究。

若考虑单一平板裂隙模型，裂隙垂直渗流方向宽度为ω，裂隙宽度为b，裂隙渗流方向长度为l，则裂隙的空间体积为V=bωl，若裂隙内部充填介质孔隙率为m，则裂隙内部孔隙体积为V=mbωl，相应充填介质骨架体积为V=(1-m)bωl。根据KARMANKOZENY 等提出的毛细管渗流等效模型建立充填裂隙渗透系数与介质性质的关系[18]，其中渗流阻力主要来自于裂隙面与充填介质颗粒表面的约束。因此，假设充填颗粒为球形其粒径为d，考虑两方面的作用，流体与阻力边界接触的有效面积为

毛细管水力半径R可以表示为孔隙体积与流体接触有效面积的比值，当充填裂隙无限延伸时，水力半径表达式为

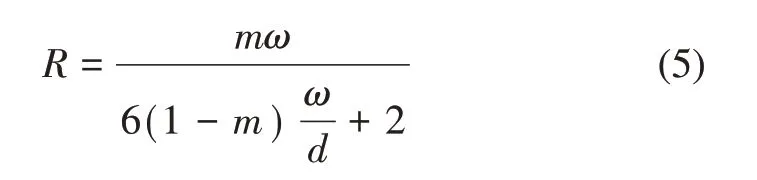
根据依明滋对阻力系数以及雷诺数的定义进一步推导可以得到充填裂隙的平均流速：

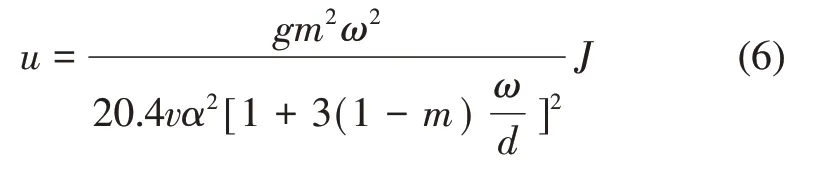
因此，充填裂隙的渗透系数与充填介质孔隙率、裂隙宽度以及颗粒表面形态的关系可以表述为

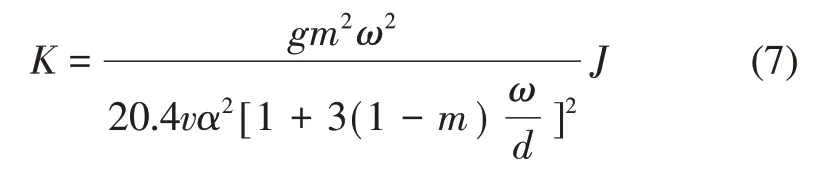
基于上述理论，与第2节提出的裂隙剪切过程接触分布模型相结合，建立考虑剪切过程岩石碎屑对裂隙渗流影响的数值计算模型。该研究基于两点假设，认为岩石碎屑均匀分布在流体中，并且碎屑颗粒为球状颗粒。因此，式(6)中颗粒形状系数α取值为1，孔隙率m随着剪切过程不断发生变化，由式(3)可以直接计算得到剪切过程裂隙空隙体积变化特征，进而裂隙渗透特性可以定量地描述。

3.2 裂隙渗流模型理论与数值求解

由于天然节理裂隙并非光滑的平行板，当裂隙面出现局部接触时，裂隙开度接近于闭合，此时，立方定律将不连续。WALSH[19]基于有效介质理论，假设裂隙面存在圆形接触区域，提出了单裂隙平行板接触模型，其表达式为

其中：bh为裂隙水力开度；bn为裂隙名义开度；ξ为裂隙接触面积与裂隙总面积的比值。通过系数项的函数关系可以看出：随着接触面积ξ增大，裂隙水力开度逐渐减小，符合流体运动的一般规律。

ZIMMERMAN 等[20]的研究结果表明，在裂隙接触面为不规则形状时，应用WALSH修正[19]公式求得的计算结果要大于实测结果，为此，将接触面的不规则性考虑到修正模型之中，提出等效水力开度计算公式：

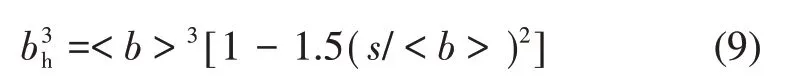
其中：s为裂隙开度在空间变化上的标准差；为裂隙开度的算数平均值。并进一步在式(9)基础上考虑裂隙接触面积影响系数(1-2ξ)，得到如下计算式：

YEO[21]在试验结果的基础上，同时考虑了裂隙岩体的开度分布以及接触面积对渗流的影响，改进后的计算式如下：

式(11)较全面地考虑了裂隙平均开度以及接触面积对等效裂隙开度的影响，但随着裂隙接触面积的增大，多种影响因素相互作用愈加明显，建立多种因素影响下的等效水力隙宽理论公式困难较大。究其原因，理论公式中接触面积所揭示的是平均影响水平，尚不能真实描述其接触形态的随机分布。因此，建立能够真实刻画剪切过程接触面积变化对渗流特性影响的数值计算模型尤为重要。

Reynolds方程在数学形式上较为简单，且能充分考虑裂隙隙宽分布的不均匀性，其在裂隙渗流分析方面具有独特的优势。当岩体裂隙中流速较小，裂隙表面起伏程度相对平缓时，其内部流体流动可以用雷诺方程描述，可避免求解繁琐的Navier-Stokes方程。肖维民等[10]阐明了其在粗糙裂隙渗流方面的适用性。若节理的隙宽分布为已知量，则方程中只有水头压力为未知量，在复杂边界条件下可以得到很好的数值解。

在稳态求解条件下，雷诺方程控制裂隙中的流体流动方程表述如下：

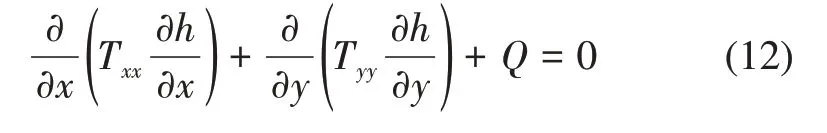
其中：Q为源汇项；Txx和Tyy分别为x和y方向的水力传导系数。

裂隙的导水系数与水力传导率及其隙宽存在如下关系：T(x,y)=ωK，基于此即可建立裂隙剪切过程接触面分布、剪切碎屑与水力传导系数定量关系，将前述渗流基本模型代入控制方程，针对特定工况下的渗流模型进行数值求解。

4 数值计算模型的有效性验证

该研究所建立数值计算模型的有效性直接关系到下文求解渗流规律的正确与否，因此，需要开展模型的有效性验证。

代表性选取裂隙面的分形维数为2.2，初始裂隙宽度分别为0.10Δ，0.15Δ和0.20Δ的隙宽模型，同时将裂隙入口设置为定压边界，水力梯度为2进行验证分析。

通常裂隙渗流规律的研究是基于对出口处渗流量的观测，因此，该研究将渗流量的求解结果作为重要参数，代入立方定律进行等效水力隙宽的求解，立方定律表达式为

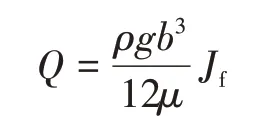
其中：μ为流体的动力黏滞系数；Jf为裂隙渗流方向的水力梯度。

将数值计算结果(bcalc)与式(11)的理论结果(btheory)相比较，如图3所示。从图3可以看出：在裂隙剪切位移比率小于1.2%的阶段A，等效隙宽数值计算结果与理论结果具有较高的吻合度；随着接触面积增大，在阶段B中，两者计算结果差别逐渐增大，甚至渗流规律完全不同。因此，在裂隙具有初始隙宽、接触面积较小且裂隙贯通性较好的情况下，两者计算结果较吻合；随着剪切位移增大，接触面积逐渐增大，理论结果的局限性凸显，求解结果存在一定误差。此外，当裂隙的初始隙宽增加至0.20Δ时，随着剪切位移增大，数值计算结果略小于理论计算结果，整体而言，数值计算结果与理论结果相差较小，说明随着初始隙宽增大，裂隙面的剪切接触面积变小，对渗流规律的影响逐渐减弱。由于计算方法的本质没有发生变化，说明该研究所提出的数值计算模型是合理的，为进一步开展裂隙渗流数值计算研究奠定了基础。

图3 等效水力隙宽数值与理论结果比值变化曲线Fig.3 Ratio of equivalent hydraulic fracture width

5 计算结果分析与讨论

5.1 接触面积影响下的渗流计算结果

为研究岩体裂隙在一定初始开度条件下的剪切渗流特性，利用第2节建立的接触分布模型进行流体计算分析。具体计算模型设置如下：分形维数分别取值2.2，2.3，2.4，2.5 和2.6 表示裂隙面的随机粗糙度，剪切位移比率由0.39%增加到3.91%进行研究，初始裂隙开度统一取值为0.15Δ。该研究主要针对法向位移较小且存在局部接触的裂隙岩体，按照该研究提出的计算方法接触面积计算结果如图4所示。从图4可知：随着剪切位移的增大，不同初始隙宽以及不同粗糙度的裂隙接触面积逐渐增大并趋于稳定，存在明显的平衡阶段。在相同剪切位移条件下，0.10Δ初始隙宽模型相对接触率增加比率比0.15Δ初始隙宽模型的高；在相同裂隙初始开度条件下，随着裂隙表面粗糙度增加，相对接触率整体升高，并且初始接触率也明显升高，主要因为裂隙表面越粗糙单位剪切位移发生剪切接触的频率越高。

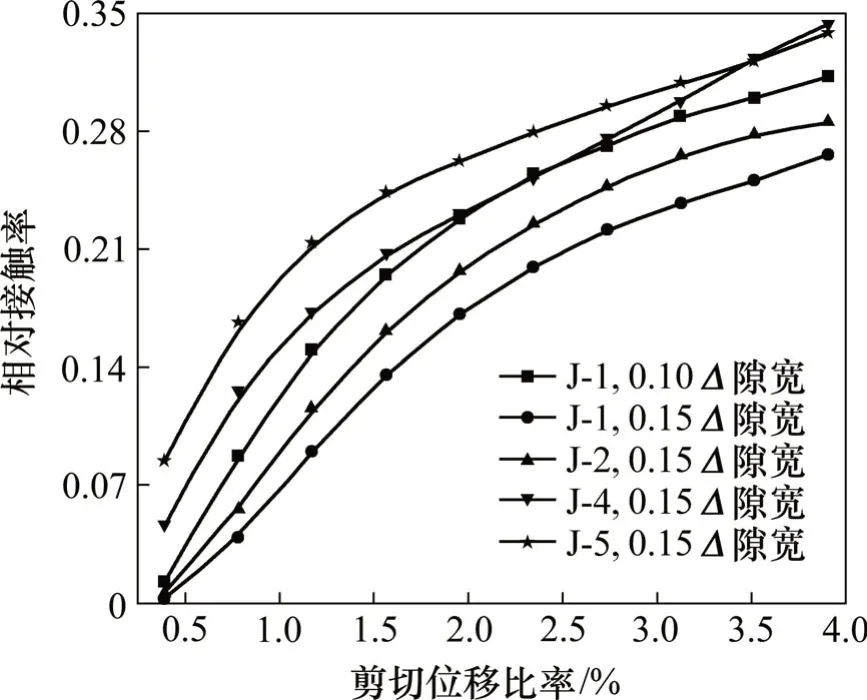
图4 剪切过程接触面积变化曲线Fig.4 Curves of contact area in shear process

同样的压力边界条件，开展不同裂隙粗糙度的渗流计算分析，对裂隙出口流量进行监测，对比剪切过程不同模型出口流量，如图5所示。从图5可知：在剪切位移初期，不同裂隙粗糙度模型计算结果规律性较强，与图4接触面积变化规律相比，出口流量的稳定趋势并不是绝对稳定，处于一种波动稳定状态。渗流体积流量均由较高水平逐渐减小到稳定流量，稳定渗流体积流量分别为初始状态的45.0%，44.8%，0.20%，23.9%和13.7%，呈现出随着裂隙表面粗糙度增加，渗流体积流量减小愈加明显之势。

控制相同的剪切位移，当剪切位移比率为0.78%时，不同粗糙度变化引起的体积流量减小量分别为13.7%，16.5%和37.4%；当剪切位移比率为1.56%时，相同粗糙度变化引起的体积流量减小量分别为10.3%，29.9%和64.2%，渗流体积流量随着裂隙粗糙度的增加而减小，增加相同的分形维数(以分形维数为2.2，2.3，2.5和2.6进行分析)，体积流量减小越明显。若剪切位移比率大于1.56%，则对于任意粗糙程度的裂隙，其相对接触率一般大于15%，此时，渗流体积流量将出现较大变化。

出现上述渗流规律的原因主要是随着接触面积的增大，渗流路径逐渐调整，裂隙局部出现闭合，而之前闭合的裂隙错位张开；另一方面，随着裂隙粗糙度的增加，渗流路径变长，等效渗流梯度减小，裂隙出口处流量整体减小。

对于分形维数为2.4的J-4模型渗流体积流量整体变化规律与其他模型的变化规律基本一致，其异常之处在于剪切位移比率超过0.78%后出口流量出现陡降，剪切过程结束时，流量几乎减小到0，而此时裂隙相对接触率为19.3%～29.2%，与渗流特征不符，对其渗流过程进行重点分析，对比剪切位移比率为0.78%，2.34%及3.13%时隙宽变化以及流线分布(如图6所示)。正是剪切过程渗流通道的调整，裂隙局部大面积接触导致渗流通道阻塞，若采用式(11)进行等效水力开度计算，其计算结果将与实际结果存在较大偏差，这也说明了理论公式的局限性，以及建立裂隙剪切渗流数值模型的必要性。

图5 不同裂隙粗糙度的裂隙渗流计算Fig.5 Fracture seepage calculation of different fracture roughness

5.2 剪切过程流动方向对渗流规律的影响

对裂隙渗流的研究通常假定渗流方向与剪切位移方向一致，在实际工程中特别是复杂的地下工程，渗流方向与裂隙岩体剪切方向无必然联系，因此，该研究分别选取裂隙渗流与剪切方向一致、完全相反以及两者方向垂直3种工况进行研究。

三者均选取0.15Δ初始隙宽模型，并且利用表面分形维数为2.2和2.5裂隙模型对比分析，数值计算结果如图7所示。从图7可知：随着岩体裂隙的剪切运动，内部渗流通道不断调整，一旦渗流通道形成，在剪切方向将不再受流体流入流出边界的影响，因此，裂隙渗流方向与剪切方向一致和完全反向这2种工况下的渗流规律基本一致。

对于渗流边界出现90°调整的工况，渗流特征出现较大差异，就分形维数为2.2的裂隙模型而言，当渗流方向调整为自下而上流入时，出口流量却由原来的逐渐减小变为逐渐增加，增加趋势愈加明显，说明随着剪切位移的变化，沿着剪切方向裂隙渗流通道趋于闭合，而垂直剪切方向等效裂隙开度逐渐变大，渗流通道沿垂直剪切方向较剪切方向更为顺畅；对于分形维数为2.5 的裂隙模型，将渗流方向调整为垂直剪切方向，其出口流量在剪切初始便大幅度减小，在整个剪切过程中维持较低水平，表明该裂隙模型渗流通道沿剪切方向十分顺畅，条形接触区域成为自下而上渗流路径的障碍。

5.3 裂隙剪切碎屑对渗流规律的影响

根据第4节建立的充填裂隙渗流计算模型，分别计算在不同剪切位移下考虑裂隙剪切碎屑与不考虑裂隙剪切碎屑对渗流规律的影响。该研究对比分析初始裂隙宽度分别为0.10Δ和0.15Δ模型，计算结果如图8所示。从图8可见：整体而言，裂隙面剪切碎屑对裂隙渗流存在较大影响，初始隙宽越小，对裂隙出口流量影响越大；对于0.10Δ隙宽模型，随着剪切位移逐渐增大，出口流量趋于稳定，其值约为未考虑裂隙碎屑模型出口流量稳定值的27.1%；同样，对于0.15Δ隙宽模型，变化规律与0.10Δ隙宽模型的变化规律基本一致，出口流量稳定值大约为未考虑裂隙碎屑模型的32.4%。

该研究建立的数值计算模型充分考虑了多种因素对裂隙渗流的影响，计算结果进一步证实了影响裂隙渗流规律的主要因素除了初始裂隙宽度、裂隙面的粗糙度以及剪切过程裂隙的接触面积外，裂隙岩体剪切碎屑对渗流规律的影响不容忽视。

图6 剪切过程隙宽变化以及流线分布Fig.6 Fracture width changes and streamline distribution in shear process

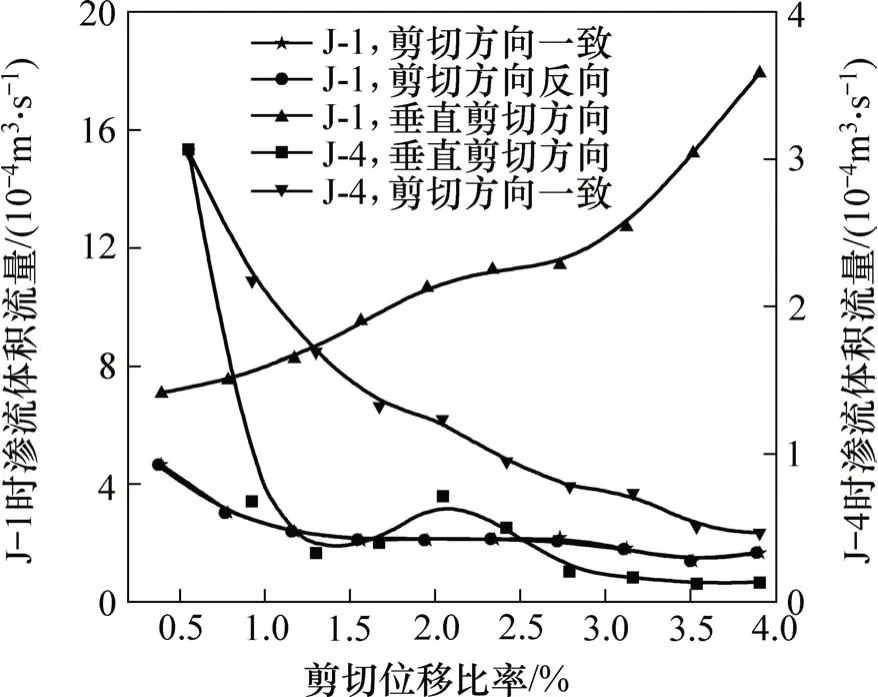
图7 渗流方向改变对出口流量的影响Fig.7 Influence of seepage direction

图8 裂隙剪切碎屑对渗流规律影响Fig.8 Influence of fracture shear debris on seepage law

6 结论

1) 基于功率谱密度理论，采用逆傅里叶变换方法构建不同分形维数的粗糙面，建立不同粗糙度的节理裂隙模型。根据雷诺控制方程，提出一种考虑剪切接触与碎屑充填的裂隙渗流模型，在工程尺度上分别研究初始裂隙宽度、裂隙面的粗糙度、剪切过程裂隙接触面积以及剪切碎屑对渗流的影响。

2) 通过对裂隙等效水力宽度的计算，当裂隙相对接触率低于15%时，理论公式计算结果与数值计算结果具有较高的吻合度；随着接触面积的增大，两者计算结果出现较大偏差。当分形维数为2.2，2.3，2.5和2.6时，裂隙粗糙度模型分析结果显示稳定渗流体积流量分别为初始状态的45.0%，44.8%，23.9%和13.7%，呈现出增加相同的分形维数，渗流体积流量减小愈加明显之势。分形维数为2.4 的裂隙模型接触率变化范围为19.3%～29.2%，但稳定体积流量仅为初始状态的0.20%，表明剪切过程裂隙接触面积对渗流的影响与其分布状态密切相关，其影响程度远大于单纯接触面积变化的影响。渗流方向与剪切位移方向对渗流的影响同样是通过改变裂隙接触分布状态实现，优势导水通道对渗流规律的影响起主导作用。此外，由于随着裂隙接触面积增大，渗流路径逐渐调整，裂隙局部出现闭合，而之前闭合的裂隙错位张开；另一方面，随着裂隙粗糙度增加，渗流路径变长，等效渗流梯度减小，裂隙出口处流量整体减小。

3) 针对裂隙剪切过程产生的岩石碎屑对渗流规律的影响进行探索研究，2种工况下出口流量稳定值分别为未考虑裂隙碎屑充填模型的27.1%和32.4%，且裂隙初始宽度越小，影响越显著。在该研究条件下验证了数值计算模型的适用性及必要性，该数值计算模型综合考虑了影响渗流规律的主要影响因素，可为后续工程尺度的裂隙渗流研究提供依据。