高超声速飞行器多约束再入轨迹快速优化

梅映雪，冯 玥，王容顺，吴了泥，孙洪飞

(厦门大学航空航天学院，厦门 361102)

0 引 言

高超声速飞行器在战术意义上以其极高的飞行速度和大跨度的飞行空域，占据着得天独厚的优势，目前已经日益受到世界各国的普遍重视[1]。黄长强等[2]提出了高超声速飞行器轨迹优化的重点研究方向，根据兵力投送和长航程的实际作战需求，势必要考虑多预设区到达和禁飞区规避，以及如何提高轨迹优化的计算效率等问题。因此有必要根据实际需求寻求一条适合再入滑翔飞行且高超声速到达的最优轨迹。

高超声速飞行器的轨迹优化涉及众多非线性约束条件，是一类复杂的非线性多约束最优控制问题[3]，其求解具有相当的挑战。自二十世纪后期,出现了多种飞行器轨迹优化方法[4]，Gauss伪谱法作为一种基于全局插值多项式的直接配点法，它相对于一般直接配点法的优势是可以用较少的节点获得较高的精度[5-7]，且计算效率较高，因此受到研究者的青睐。Reddien[8]使用Gauss伪谱法求解最优控制问题，利用全局正交多项式在特定节点同时离散状态量和控制量。李铁鹏等[9]基于Gauss伪谱法以飞行时间为优化指标对滑翔弹道进行了优化设计。和争春等[10]在过载限制条件下对升力体高超声速飞行器再入弹道进行了优化设计。上述文献多将重点放在如何优化得到高超声速飞行器在各种常规约束条件下到达指定点的轨迹上，却很少考虑飞行器在实际任务中必须面对的经过特定任务区域并顺利避开敌方拦截或勿入区域的场景。对于绕飞区这一导弹防御系统的挑战，大都采用改变倾侧角符号的方法单独规划横向轨迹。张科南等[11]基于一定的倾侧角变化规律优化得到了高超声速滑翔飞行器规避拦截区的再入轨迹，但计算效率和鲁棒性均不高。Shen等[12]所述方法能够快速计算出一条满足各种过程约束和状态约束的三维再入轨迹，但其横向轨迹设计部分仅通过一次改变倾侧角的符号进行控制，不太适用于大范围横向机动情况。也有学者对Gauss伪谱方法进行改进，以适用于此类考虑测控区和绕飞区的复杂多约束问题。Darby等[13]提出了一种多重区间配置法对连续时间非线性优化问题进行研究，但未针对具体问题。Wang等[14]采用多段Gauss伪谱法通过将航路点和绕飞区分别设置为固定LG点和虚拟LG点的方法对此类问题进行研究，但设定LG点的方式无法使轨迹得到全局优化。Jorris等[15]提出了一种实时自主优化方法使得轨迹在满足航路点和绕飞区等复杂多约束的同时再入时间最短，但未考虑测控区以及轨迹平滑性这样的实际问题。因此，在如此多约束条件下进行轨迹的优化设计是一个比较复杂的问题，需针对轨迹优化问题的特点，采用合适的优化策略和方法。

考虑到滑翔飞行方式可以规避拦截和进行防御，而飞行器再入初期不满足滑翔条件，通常将再入轨迹分为初始下降段和准平衡滑翔段分别规划。本文在此基础上，考虑到实际任务中所必须面对的经过特定任务区域并顺利避开敌方拦截或勿入区域的场景，对高超声速滑翔飞行器轨迹优化的主要约束条件进行了分析并给出相应的数学模型，然后对Gauss伪谱方法在求解复杂多约束条件下轨迹优化问题时存在的主要难点进行了分析，提出了具体的轨迹分段优化策略和方法，较好地解决了这一问题。为了便于控制系统操控，保证优化效率，同时为了避免约束条件太多而减小可行域，在性能指标中引入弹道倾角和航向角相关指标的加权和代替控制角速率等相关过程约束。最后通过对比，分析了本文优化方法的快速性和工程实用性。

1 问题描述和预备知识

1.1 问题描述

高超声速飞行器再入段由再入点到滑翔段终端点，轨迹规划过程需要考虑动力学方程约束，过程约束，终端约束等常规约束，还要考虑更符合实际任务的测控区约束和绕飞区约束。

1) 模型约束

(1)动力学方程约束

高超声速飞行器在高速大气层内无动力返回，由于高升阻比飞行器气动力和地球重力分别约为科氏惯性力和地球自转引起的惯性离心力的100倍和1000倍[16]，因此可以假设地球为圆球不旋转模型，高超声速飞行器无量纲三自由度运动方程[17]为：

(1a)

(1b)

(1c)

(1d)

(1e)

(1f)

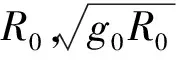
无量纲升力L、阻力D分别为：

(2)

式中：Sref为飞行器气动参考面积；CL,CD分别为升力系数和阻力系数，由飞行器的攻角α和Ma决定；ρ为大气密度。

(2)过程约束

为保证再入飞行器在结构和热防护上的可靠性，再入过程要求严格满足驻点热流密度、动压和法向过载约束[18]，即:

(3a)

(3b)

(3c)

(3)控制约束

以飞行攻角α和倾侧角υ为控制变量，为了满足飞行器控制能力要求，有如下约束条件[18]：

(4)

式中：μ1,μ2为攻角取值范围的上、下限；κ为倾侧角取值范围的上限。

(4)终端约束

为保证在一定的落角(终端弹道倾角)和速度下将飞行器引导至指定终端目标位置，通常要加上如下终端约束[19]：

(5)

式中：tf为终端时刻。

以上是高超声速飞行器轨迹优化常见的约束条件，本文考虑到工程上的实际需要，在常规约束基础上还要考虑测控区约束和绕飞区约束。测控区和绕飞区约束描述如下：

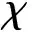
Θ(λ,φ;λc,φc,Rc)d(λc,φc),Γ)-Rc<0

(6)

Ξ(λ,φ;λr,φr,Rr)d(λr,φr),Γ)-Rr≥0

(7)

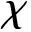
2) 性能指标

在高超声速飞行器再入轨迹优化的研究中，多数文献仅仅考虑某个单一的性能指标。例如文献[20]，为了实现快速打击，要求再入飞行时间最短，所以将再入过程的时间作为优化目标：

J1=tf-t0

(8)

式中：t0为再入初始时刻。

为了兼顾到再入轨迹的平滑性，常常将弹道倾角速率的平方的积分作为性能指标[21]：

(9)

再者，为了便于控制系统操控，使飞行器平稳飞行，也有学者采用航向角速率的平方的积分作为性能指标[22]：

(10)

本文将综合考虑所设计轨迹的高效性和工程实用性，选择式(8)，式(9)，式(10)所示性能指标的加权和作为优化目标，通过调整权系数，能够在时间最优、控制量最优和轨迹平滑性最优之间进行权衡，以规划出易于实现的轨迹。最终的性能指标式为：

J=w1J1+w2J2+w3J3

(11)

式中：w1,w2,w3为权重系数，用于调节优化指标中飞行器飞行时间以及弹道和控制量平滑性最优之间的权重。

注1. 对于性能指标的分析：从物理机理上，采用Gauss伪谱法将再入时间(tf-t0)作为目标函数，即要求再入时间最短，同时在性能指标中引入弹道倾角和航向角相关指标代替相关过程约束使纵向轨迹和横向轨迹平滑，由于减少了约束条件数量，计算效率进一步提高；从控制机理上，w1,w2,w3分别为性能指标J第1、2、3项的权，当权越大，惩罚越大，对应项的函数值越小，即对应项越优。对于线性系统，权的选取可借鉴LQR方法中加权矩阵的选取[23-25]；而对于非线性系统，目前更多依赖于工程实际。为了方便后续制导工作，相对于轨迹平滑性，再入时间是次要的，因此w2、w3都要较w1取大一些。

令x,u分别表示系统(1)的状态和输入，即：

x=[x1,x2,x3,x4,x5,x6]T=[r,λ,φ,V,θ,ψ]T；u=[u1,u2]T=[α,υ]T；再令f(x,u)为状态方程(1a)～(1f)的右端函数。

则本文所要研究的多约束问题可描述为：

在满足动力学方程约束(1a)～(1f)，过程约束(3a)～(3c)，控制约束(4)，终端约束(5)以及测控区约束(6)和绕飞区约束(7)的情况下，寻找合适的状态轨迹和控制输入，以及初末时刻(若未给定)，使得性能指标(11)最小，即：

(12)

式中：W=6,M=2；Ωζ(x,u)≤0为由过程约束(3a)～(3c)、控制约束(4)确定的q个不等式约束；Λ(x(tf))≤0为由终端状态约束(5)确定的等式及不等式约束。

上述多约束轨迹优化问题本质上是最优控制问题，工程上普遍使用GPM来求解最优控制问题的数值解[26]。但是，由于测控区约束为局部性约束，而GPM仅对具有过程约束的最优控制问题有效。因此，测控区甚至是多个测控区约束的存在加大了求解轨迹优化问题的难度，本文将着重解决该问题。

1.2 预备知识

Gauss伪谱法以Legendre多项式的根为离散点，将连续最优控制问题的状态变量和控制变量离散化，并以离散点为节点采用全区间Lagrange插值多项式来近似状态变量和控制变量，从而将轨迹优化的最优控制问题转换为非线性规划问题进行求解[27]。

在不考虑测控区和绕飞区的情况下，问题可以直接采用GPM求解。对于GPM的一般步骤，本文作如下归纳：

1) 对时间变量t作变换，将时间区间转换到[-1,1]。

(13)

2)确定离散时刻点。

取N阶Legendre多项式的N个根τk∈(-1,1),k=1,2,…,N，再令τ0=-1,τN+1=1，则τ0,τk,τN+1构成弹道的N+2个离散点。

3)约束条件及性能指标的离散化。

根据上述时间变换和配点选取，构造系统状态x和输入u关于其估计值X,U的近似表达式：

(14)

令Xk=X(τk),Uk=U(τk)；J=w1J1+w2J2+w3J3φ(t0,tf)+η(x(t),u(t),t)dt，其中，则微分方程约束，等式/不等式约束以及目标函数经离散化，可转换为下述代数约束[28-29]：

(15)

Ωζ(Xk,Uk)≤0

(16)

Λ(X(tf))≤0

(17)

(18)

经过对时间、非线性函数、微分方程等离散化后，最优控制问题(12)(不考虑测控区和绕飞区约束)就转化为如下离散非线性规划问题：

求离散节点上的状态X(τi)(i=0,…,N)和控制变量U(τi)(i=1,…,N),使得性能指标(18)最小，并满足动力学方程约束(15)，过程约束等不等式约束(16)以及终端状态约束(17)。

2 轨迹优化策略

目前许多研究采用Gauss伪谱法解决高超声速飞行器轨迹的优化设计问题，但在面对本文提出的多约束任务场景时，考虑到测控区约束的局部性特点，无法直接求解。

2.1 多约束分段优化方法

假设1. 飞行任务中有l个绕飞区，n个测控区。飞行器自东向西跨经度飞行且测控区中心轴处在不同的经度上。同时假设所有测控区均在准平衡滑翔段。假设1具有一般性，对测控区位置的假定是方便对测控区自东向西进行编号。若部分测控区的中心轴处于同一经度，则以该经度对轨迹进行分段，然后按照纬度对处于相同经度的测控区编号。不妨假设，经过编号后的测控区按照自东向西的方向依次为测控区1、测控区2, ……，测控区n。

对于绕飞区约束和测控区约束，将问题简化，只考虑其横向剖面，化三维约束为绕飞圆约束和测控圆约束进行求解。则规避绕飞区，进入测控区两个约束条件可分别严格描述为：

(19)

(20)

式中：下标ri和cj分别表示第i个绕飞区和第j个测控区。

注2. 本文分段点个数取决于测控区个数，自然地，测控区越多，分段数越多，对数值计算要求越高，但计算时间可接受，并不会带来明显的增长。

由式(19)可知，绕飞区约束是一个全局性约束条件，即：对于轨迹上所有点(λ,φ),都满足Ξ(λ,φ;λri,φri,Rri)≥0。因此，可以直接将其设置为过程约束。则规避第i个绕飞区的约束为Ξi(λ,φ;λri,φri,Rri)≥0。

由此可见，绕飞区约束作为全局性约束条件不会给求解带来本质上的困难。由式(20)可知，测控区约束仅仅是对轨迹的局部性约束，此时不能将其作为过程约束来看待，这给轨迹优化问题带来了本质困难。针对该棘手问题，本文将改进传统Gauss伪谱法，以适用于再入飞行任务含测控区的轨迹优化问题。具体来说，就是依据n个测控区将准平衡滑翔段分成n+1段，这样连同初始下降段，相当于将整个轨迹分割成n+2段(如图1所示)，然后每一段轨迹通过Gauss伪谱法来求解。为方便，自东向西依次称每一小段轨迹为第1段、第2段，……，第n+2段。

将飞行轨迹按上述方式进行分段后，最主要的问题是分段点如何选取。分段点选取首先要考虑飞行器在每一段上的飞行要求和约束，还要兼顾到Gauss伪谱法的适用性。下面给出分段点的选取依据。

分段点1为初始下降段与准平衡滑翔段的交界点。该点可以通过平衡滑翔条件以及最大热流密度约束(再入初期动压和过载一般较小，可以满足约束，因此不考虑)来决定，即满足条件[29]：

(21)

分段点2～(n+1)根据测控区约束选取，将第j个测控区约束设置为第j+1段轨迹的终端约束。根据测控区位置及大小，动态设置轨迹上点Aj为分段点。设Aj点所在经纬度坐标为(λAj,φAj)，若Aj点位于测控区内部，即：进入第j个测控区的约束为Θj(λAj,φAj;λcj,φcj,Rcj)<0，则轨迹成功经过测控区域，符合任务要求。

令*(p)表示第p段弹道对应参数，p∈{1,2,…,n+2}。

在每段轨迹上选择合适数量的离散点将状态变量和控制变量进行离散化，将整个轨迹分段离散化后，将所有的离散点状态变量、控制变量作为优化参数同时进行优化设计，最终通过插值获得对应的最优控制及最优轨迹，第p段弹道优化问题描述如下:

当然，为确保状态量和控制量的连续性，在轨迹优化过程中各段轨迹在分段点处需要满足如下连接条件：

(22)

2.2 优化流程

本文采用GPM作为每阶段优化的基本方法。根据上述优化策略，为充分利用再入轨迹不同阶段特性,将再入轨迹分为初始下降段和滑翔段分别优化，同时根据测控区约束条件将滑翔段分段，将一般最优控制问题转换为多段最优控制问题，以求得满足多约束条件且具有一定精度的最优轨迹。图2描述了本文提出的分段优化策略的基本流程。

3 仿真结果及分析

在MATLAB中进行仿真，仿真的目的是检验任意给定测控区和绕飞区的情况下，所设计的方法是否能够快速得到优化轨迹使飞行器从再入点快速平滑地过渡到终端点，且成功进入测控区并规避所设绕飞区；同时就优化效果与已有研究进行对比，检验本文所设计的改进方法的高效性和实用性。

3.1 算例

以通用航空器CAV为对象，再入飞行器气动特性参数采用通用航空器CAV的相关参数[30]，其最大升阻比为3.4，气动参考面积为0.8 m2，质量为900 kg，最大升阻比攻角为12°。

根据实际要求，仿真参数设置如下：

假设飞行器要进入1个测控区并绕过3个绕飞区，即，n=1,p=3。

给定测控区1中心位于(136.11°E，44.74°N),半径为100 km；绕飞区1中心位于(140.03°E，35.53°N)，半径为600 km；绕飞区2中心位于(123.91°E，53.98°N)，半径为500 km；绕飞区3中心位于(116.37°E，39.690°N)，半径为1000 km。

性能指标的权重系数取为w1=0.2,w2=0.4,w3=0.4。

图3～6为采用本文提出的改进Gauss伪谱法对算例进行的有效性验证曲线。由图3可知，再入过程中热流密度、法向过载以及动压都严格低于最大峰值，满足常规过程约束。图4为高度、速度关于时间变化的曲线，从图中可以看出，曲线平滑且满足终端状态约束等条件。图5表明控制变量在要求范围内变化，且变化较为平缓。但根据实际工程需要，由于考虑攻角幅度限制，导致出现了两次较长时间的攻角饱和。

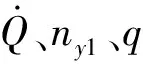
步增加，α先上升维持饱和值30°使得V先下降以满足测控/绕飞区约束以及终端高度等约束，后下降以满足终端速度等约束，同时υ需配合α呈先上升后下降的趋势以满足测控区约束等多约束条件。

图6为轨迹的横侧向和三维轨迹图，目的是便于观察轨迹的横侧向走向，图6(a)、图6(b)表明轨迹成功进入测控区并且有效规避了绕飞区，最后到达终端点，且在分段点处状态量和控制量平滑衔接。

为验证测控区/绕飞区数目对模型维数的影响，在上述算例的基础上增加两个测控区，中心分别位于(130.11°E，40.74°N)、(126.04°E，32.83°N),半径都为100 km，分别记为测控区2和测控区3，统计计算时间，如表1、表2、表3。

表1 测控区个数对计算时间的影响Table 1 Influence of the number of monitoring zones on the calculation time

表2 绕飞区个数对计算时间的影响Table 2 Influence of the number of no-fly zones on the calculation time

表3 绕飞区分布/大小对计算时间的影响Table 3 Influence of the distribution of no-fly zones around the calculation time

从表3中可以看出：1)测控区个数的增加会延长计算时间t；2)绕飞区个数对计算时间有影响，但不显著，绕飞区的分布及大小对计算时间的影响更大。

这说明由于本文分段点个数取决于测控区个数、自然地、测控区越多，分段数越多，对数值计算要求越高，但计算时间可接受，并不会带来明显的增长；而绕飞区只是作为过程约束，绕飞区的数目确实对模型的维数造成了影响，但计算时间更大程度上会受到绕飞区分布及其大小的影响，若分布过于紧密或者绕飞区较大，轨迹曲度可能发生较大变化，对在线规划势必会造成影响。

文献[27]考虑到快速打击和轨迹平滑性，引入再入时间和弹道倾角相关指标的加权和作为目标函数。本文在此基础上考虑到轨迹快速优化要求，力求控制量变化平缓，同时为了避免约束条件增多减小可行域，在目标函数中引入航向角相关指标代替在过程约束中增加控制角速率约束，取再入时间、弹道倾角和航向角相关指标三项指标加权和作为目标函数。图7至图8为采用文献[27]中性能指标与本文改进性能指标下对原算例(n=1,p=3)进行的优化对比曲线。图7表明，两种情况下常规过程约束都能被控制在峰值之内，但改进方法使得热流率、法向过载和动压在再入过程中明显低于未改进方法，从而减小了飞行器承受能力，提高了飞行器性能和使用寿命。图8表明改进方法下的控制变量变化曲线较未改进方法平滑，波动明显更小，从而便于控制系统操控，极大地提高了计算效率。表4为采用两种优化方法所需计算时间的对比表，改进方法计算效率较未改进方法大大提高，更加满足再入飞行任务快速规划的需求。

计算方法计算时间/s改进38.974302未改进453.015268

4 结 论

本文针对高超声速飞行器再入过程中面临多个测控区和绕飞区的再入轨迹设计问题，分析了采用传统Gauss伪谱法设计时存在的主要问题，引入了分段优化的轨迹设计思路，并提出了具体的轨迹分段策略。以再入时间、弹道倾角以及航向角相关指标的加权和最小为性能指标设计了考虑各种约束条件下的最优轨迹。仿真结果表明本文所设计的改进方法能够快速有效的用于解决任意给定测控区和绕飞区约束的轨迹优化问题。