基于Matlab的改进自适应算法性能分析

毛耀东

摘要：变步长自适应滤波算法通过对误差和步长因子建立函数关系，在误差大的时候使用大步长来加快收敛速度，误差小的时候使用小步长保证收敛稳定性。为了进一步提高算法性能，在原有函数模型的基础上，提出一种基于Sigmoid函数的新的变步长LMS（Least Mean Square，最小均方误差）算法，并通过仿真确定各参数的最佳取值。仿真结果表明，和现有的变步长滤波算法及传统固定步长算法相比，在收敛速度和滤波效果上有了明显的提高。

关键词：自适应算法;变步长;最小均方;Sigmoid函数;收敛性能

中图分类号：TP301   文献标识码：A

文章编号：1009-3044（2019）16-0266-05

开放科学（资源服务）标识码（OSID）：

Abstract： The variable step size adaptive filtering algorithm establishing a functional relationship between the error and the step size factor. When the error is small， the small step length is used to ensure the convergence stability.otherwise，large step size is used to accelerate the convergence speed by  In order to further improve the performance of the algorithm，On the basis of the original function model， a new variable step size LMS （Least Mean Square） algorithm based on Sigmoid function  is proposed， and the optimal values of each parameter are determined by simulation. The simulation results show that compared with the existing variable step size filtering algorithm and the traditional fixed step size algorithm， the convergence speed and filtering effect are obviously improved.

Key words： adaptive algorithm; variable step size; least mean square; Sigmoid function; Convergence performance

自适应滤波器是能够自动调节参数的滤波器，其参数会随着环境的变化而变化。主要应用场景为系统辨识，信道均衡，信号增强和预测。随着微电子等硬件技术的高速发展，自适应滤波器技术也不断完善。相比于经典滤波，自适应滤波不需要知道太多的先验信息[1]，因而其应用范围更为广泛。自适应滤波中最具代表性的是LMS算法和RLS算法。LMS算法计算量小，但是收敛速度慢。虽然RLS算法的滤波效果和收敛速度比LMS算法好，但是在滤波器阶数较大时，RLS算法的计算量很大，为O[[n2]]。因此提出一种在算法收敛过程中自动调节步长因子的变步长LMS算法，该算法以Sigmoid函数为模型，与现有变步长LMS算法相比，误差小的时候，步长具有更小的变化率，因而收敛稳定性进一步提高。

1 自适应滤波算法的原理分析

1.1 自适应滤波器的一般结构

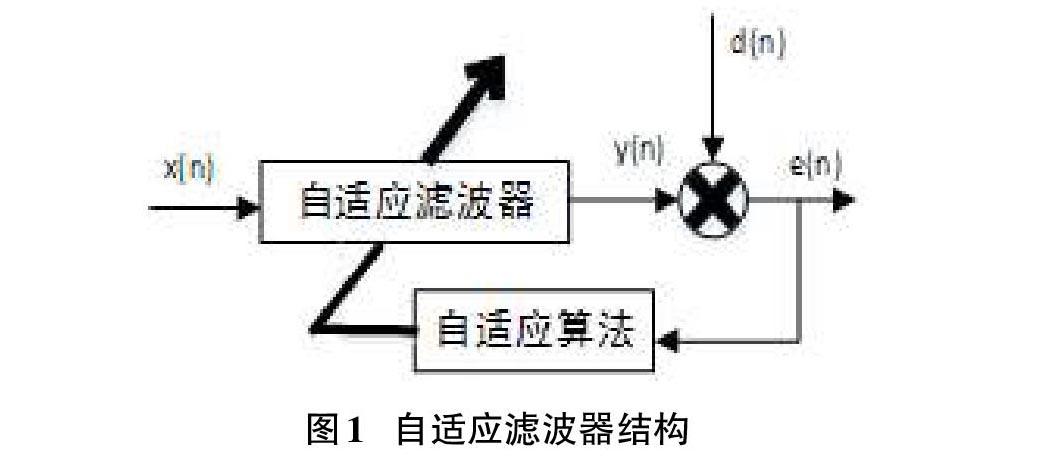
自适应滤波器一般是阶数固定的横向滤波，它包括四个端口：n时刻的输入信号x（n），期望信号d（n），输出信号y（n）和误差信号e（n）。通过y（n）与d（n）的差e（n）来自动调节滤波器的参数，使得滤波器系数不断优化。自适应滤波器的结构如图1所示。

1.2 自适应滤波算法

自适应滤波算法有两大基本类：LMS和RLS。LMS算法中除了固定步长算法外，还有变步长的LMS算法和变换域的LMS算法[2]。前者通过在误差信号和步长之间建立函数关系来调节步长[3]，后者将时域信号正交变换得到变换域信号，并在变换域中使用自适应算法。RLS算法充分利用之前的输入矢量x（k）和d（k），通过设定一个遗忘因子来决定各时期数据的权重，来实现算法的快速收敛。

1.2.1 LMS自适应滤波算法

LMS自适应滤波器一般采用横向FIR结构，如图2所示。

各参数分别为：

X（n）为n时刻的输入信号矢量，W（n）为n时刻的滤波器系数，N为滤波器阶数。通过计算输出信号和期望信号，可得估计误差：

利用快速下降法[4]可得滤波器系数更新方程为：

U是步长因子，取正的常数。为了满足算法的收敛性，u需要满足：

1.2.2 RLS自适应滤波算法

LMS算法由于没有利用过去的信息。导致梯度估计误差大，算法收敛速度慢，如果自相关矩阵的逆矩阵不具有正定性还会导致算法发散。RLS算法在求均方误差时观测数据的长度是变化的，越久之前的数据，其权系数越小，因而RLS算法在非平稳环境下的滤波效果要由于LMS算法。RLS具体算法流程如下：

其中[SD（n）]表示X（n）自相關矩阵的逆，δ表示输入信号功率估计的倒数，[λ]表示遗忘因子，它表示之前的数据在当前时刻的影响力，距离现在越久的数据，对滤波器系数的印象里越小。因而在非平稳信号滤波方面，该算法也能有效。

2 改进的LMS算法

为了解决传统LMS算法的问题，很多变步长LMS算法被提出，文献[9]提出了一种基于小波分解的变步长LMS滤波算法，根据小波分解的多分辨率分析特性，将信号与噪声正交分解在不同的频率范围，然后对各个频段的信号进行滤波，最后重构得到滤波信号，是一种频率滤波波的算法。文献[10]提出了一种滤波器阶数可变的LMS算法，通过引入漏因子，将抽头长度假设成一个假分数进行更新，再对更新后的数值极性处理，变成真实的抽头长度，并将变步长的思想用到变抽头长度算法中。文献[11]针对可见光通信的多径干扰问题，提出一种反正切函数的变步长自适应LMS算法，通过分析室内信道模型，建立最小均方算法步长因子的函数，然后对反正切函数进行平移变换，建立了步长与误差的非线性关系。

所有这些变步长算法都能分为两类：对步长因子和误差建立函数关系并做各种变形;使步长因子随误差的自相关估计的变换而变换。前者最具代表性的是覃景繁[12]等人提出的基于Sigmoid函数的变步长算法（SVSLMS），其步长因子和误差的函数关系如下：

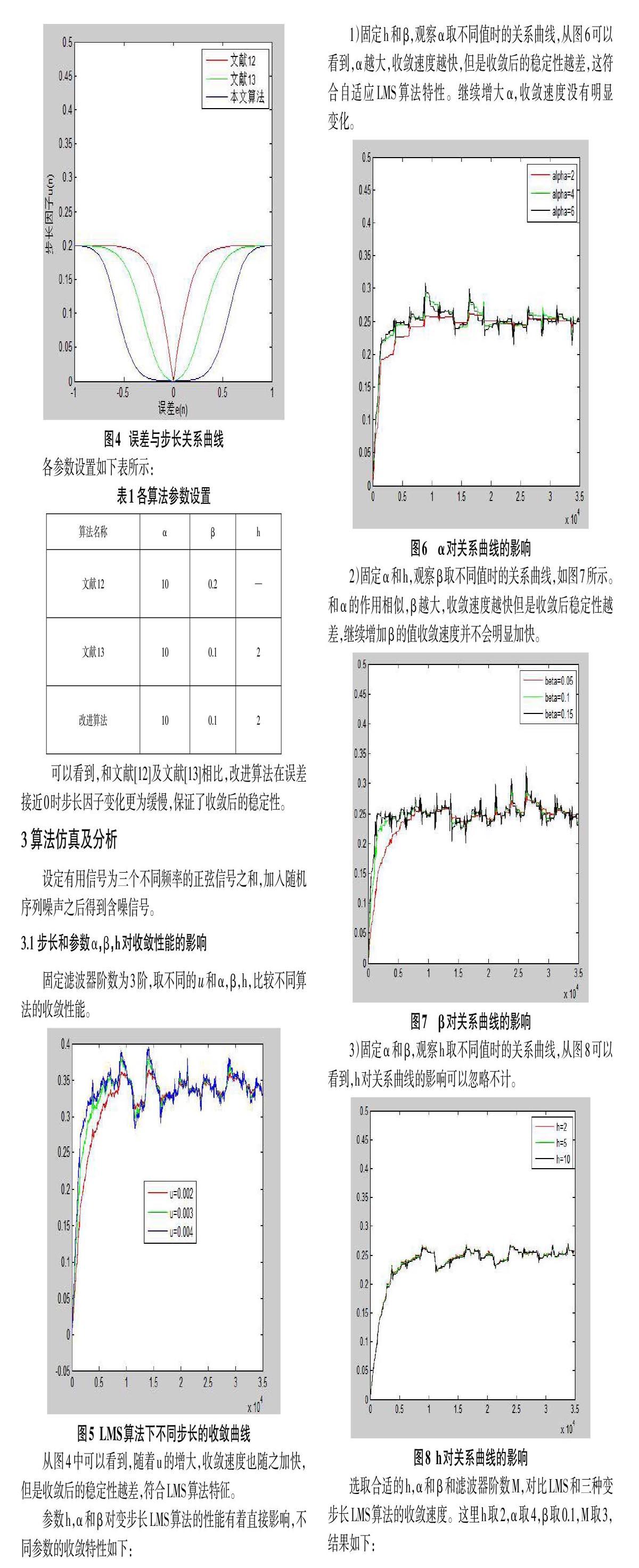
三种步长与误差因子的关系曲线对比如下：

各参数设置如下表所示：

3 算法仿真及分析

设定有用信号为三个不同频率的正弦信号之和，加入随机序列噪声之后得到含噪信号。

3.1 步长和参数α，β，h对收敛性能的影响

1）固定h和β，观察α取不同值时的关系曲线，从图6可以看到，α越大，收敛速度越快，但是收敛后的稳定性越差，这符合自适应LMS算法特性。继续增大α，收敛速度没有明显变化。

2）固定α和h，观察β取不同值时的关系曲线，如图7所示。和α的作用相似，β越大，收敛速度越快但是收敛后稳定性越差，继续增加β的值收敛速度并不会明显加快。

3）固定α和β，观察h取不同值时的关系曲线，从图8可以看到，h对关系曲线的影响可以忽略不计。

3.2 滤波器阶数对收敛性能的影响

可以看到，阶数越高，系数会越低，滤波器阶数不会影响收敛速度在收敛速度上也和上一节的结论相同。

3.3 各算法的滤波效果对比

从滤波效果图上，四种算法都能得到和原信号差不多的波形。表2直观反映了滤波性能，可以看到，文献[12]的变步长算法相比于原LMS算法，在信噪比上有明显所提高，同时RMSE也下降了下降了18%左右。基于Sigmoid函数的文献[13]在信噪比上比起文献[12]有轻微提高，同时RMSE有所下降。针对文献[13]的改进算法，和文献[13]相比，信噪比有明显提高，而RMSE也有明显下降，证明了改进算法在滤波效果上的可行性。

4 结束语

在原有变步长LMS算法的基础上，通过调整步长因子和误差的函数关系，提出一种以Sigmoid函数为模型的改进LMS算法，该算法能够保证较快的收敛速度和较强的收敛稳定性，解决了原有LMS算法在收敛后的震荡过大问题。仿真结果表明，改进的算法和已有的变步长LMS算法相比，信噪比有明显提升，而且均方误差也明显下降，因此对时变信道中的低信噪比信号能取得不错的滤波效果。

参考文献：

[1] 高建辉. LMS自适应滤波器的设计理论研究[J]. 信息技术， 2011，（8）：112-115.

[2] 耿妍，张端金. 自适应滤波算法综述[J]. 信息与电子工程，2008（4）：315-320.

[3] Raymond H K， Edward W J.  A variable step size LMS algorithm[J].IEEE Trans. on Signal Processing， 1992，40：1633-1642.

[4] 張红梅，韩万刚. 一种新的变步长LMS自适应滤波算法研究及其应用[J].仪器仪表学报，2015，36 （8）：1822-1830.

[5] Park d J. Jun B E. Self perturbing recursive least squares algorithm with fast tracking capability[J].Electronics Letter. 1992，28（6）：558-559.

[6] 常铁原，王月娟. 一种具有快速跟踪能力的改进RLS算法研究[J]. 计算机工程与应用. 2011，47（23）：147-150.

[7] Elnashar Ayman.Elnoubi Said. EI-Mikati Hamdi.Performance analysis of blind adaptive MOE multiuser receivers inverse QRD-RLS algorithm[J]. IEEE.Transactions on Circuits and Systems， 2008，55（1）：398-411.

[8] Kwang Seop Eom，Byung Eul Jun，DonG Jo Park. Fast Tracking and noise immunised RLS algorithm based on Kalman filter[J].  Electronics Letter， 1996，32 （25）：2311-2312.

[9] 段帅军.基于小波分解的变步长LMS降噪算法研究[J].软件，2018，39（12）：155-158.

[10] 雷翼龙，余涛.一种基于变抽头长度的变步长LMS算法[J].电子测试，2018（10）：55-57.

[11] 张进玉，王翀，杨宏，李国辉，赵瑶，王姣.基于反正切函数的可见光通信LMS均衡算法[J].光通信技术，2018，42（5）：59-62.

[12] 覃景繁，欧阳景正.一种新的变步长LMS自适应滤波算法[J].数据采集与处理 ，1997（3）：171-194.

[13] 陈泳，田金鹏，刘燕平.一种新的变步长LMS自适应滤波算法[J].电子测量技术，2015，38（04）：27-31

【通联编辑：梁书】