面向互联网+的混沌S盒构架与低复杂度图像加密研究
聂佳琦 吕梦如 张晓飞 王玉雯


摘要:本文提出了一种基于混沌映射构造动态S盒的加密方法。在Fridrich所提出的permutation-diffusion图像安全加密设计框架基础上,方法包括四个阶段:构造动态S盒、S盒替换、置乱与扩散。首先,提出了一种基于混沌映射联系明文的动态S盒构造方法。然后,利用基于猫映射的置乱过程提高算法的加密性能。最后,扩散过程实现雪崩效应降低加密算法的复杂度。根据不同类型的统计分析实验的结果表明,本文提出的加密方法与以前的加密方法相比更加安全、高效。
关键词:图像加密;动态S盒;混沌系统
中图分类号:TP18 文獻标识码:A
文章编号:1009-3044(2019)16-0012-02
开放科学(资源服务)标识码(OSID):
近年来,随着计算机技术以及通信技术的快速发展,数字信息被广泛地应用到社会各个领域当中。由于图像信息相关性强,冗余度高,且对于所加密的图像,要求解密图像具有高保真度,研究者们提出了一些新的针对图像的加密方案[1]。
混沌具有遍历性、混合性、确定性以及对初始条件和控制系数的敏感性等显著特点,非常适合于数据的加密。为了更好地隐藏明文信息,Y.Wang于2009年介绍了一种基于混沌的可变参数的图像加密算法。在这个算法中,产生密钥流的初始密钥由混沌映射与图像密文计算得出[2]。2011 年 Y. Wang 等提出了一种基于时空混沌的快速图像加密算法[3]。同年,M. Seyedzadeh 与 A. Mirzakuchaki 提出了一种基于分段混沌映射的快速图像加密算法[4]。2013 年澳门大学的 C. Chen 等也提出了一种基于变化参数与混沌映射的图像加密算法,体现出了混沌映射在改变图像加密系统参数,提升算法安全性方面的广泛应用[5]。
但在当前的研究中,仍存在一些未解决的问题,主要体现在:混沌虽然具有非线性的特点,但在用于S盒的构造算法时,由于S盒大小本身的限制,静态S盒在图像加密中的性能不能达到实际应用的要求;得到较高非线性度的S盒,利用更复杂的迭代系统会导致加密算法效率降低。
1 加密算法
提出利用一维Logistic映射结合明文的动态S盒构造方法,并引入置乱与扩散步骤构造加密方案。方案中利用两种混沌映射确保加密的安全性,并降低算法复杂度。构造与被加密图像相关的动态S盒,利用混沌特性很好的猫映射对明文进行置乱,扩散以达到雪崩效应。方法能够将混沌理论和S盒替换加密两种技术的优势结合在一起,提供一种随机性更强、复杂度更低的加密方案。
1.1一维Logistic映射
其数学表达式为:
1.2明文密钥建立关系
将明文输入公式(2)得到一个取值在[0,1]的数[keyi],用于构造动态S盒。
1.3构造动态S盒
[keyi]作为混沌系统的初值[x1],控制参数为3.99,生成256长度的数组与0~255的整数构建映射关系,即替换数组。由于明文不同因此构造的S盒也不同。
1.4加密步骤
Step1:输入一张图片[P(m,n)],m与n为图片像素的高度与宽度,也表现出了像素数目。
Step2:将图片矩阵代入迭代公式,得出密钥[keyi(i=1,2,...,8)]。其中, pj代表图像中第j个像素,ki(i=1,2,…,8)为用户选定的8个不同的范围在(0,1)的初始值。[keyi(i=1,2,...,8)]∈(0,1)用于生成构造动态S盒所需的密钥。
Step3:将明文分块[Bi(i=1,2,...,8)],每块大小为[m4×n2]。
Step4:构造每一明文块[Bi(i=1,2,...,8)]的S盒[S-boxi(i=1,2,...,8)]。将密钥作为初始值输入混沌系统。得到替换后图像[P1]。
Step5:利用猫映射公式如下:
对[P1]进行置乱,得到置乱后图像[P2]。
Step6:将[P2]代入扩散公式:
得到扩散后的结果[P3]。Step7:重复5次Step5,得到加密后图像,加密步骤见图。
解密步骤为加密步骤的逆步骤。
2 检验与分析
为了检验本文加密算法的性能,与其他四种图像加密算法做比较。分别为Scheme1[6],Scheme2[7],Scheme3[8],Scheme4[9]。
2.1 直方图分析
图2分析了几个平面图像的灰度直方图和图像加密后的直方图,可以看出,加密图像的直方图是均匀并且完全不同于明文各自的直方图。因此.该算法可以抵抗任何统计攻击。
2.2相关分析
计算和比较原图像和密文图像中邻域像素的相关性。计算方法如公式(5)所示:
从表1中可以看出,该加密方案产生去相关的相邻像素图像,清晰的的图像的相关系数接近1,但那些加密图像的平均相关性水平近似等于0,这表明,提出的方案对统计理论的攻击是安全的。
2.3密钥空间分析
对于一个健壮的加密方案,密钥空间必须足够大,才能使蛮力攻击不可行。在加密过程中,算法的密钥空间是指所有可能的算法的排列组合。为了考察该密钥有效抵抗攻击的能力,随机拟定一个初值,用16位十进制数表示(1位整数,15位小数),则本文算法的密钥空间为(1016)6×28×(28-1)4=2359。
2.4密钥敏感度分析
密钥敏感度分析满足了用户不受网络袭击的需求,本文做了一系列的密钥敏感度测试:用不同的尺寸加密了不同尺寸大小的灰度图像[P(M,M)],在用最初密钥加密的图像和在这种情况下加密的图像的不同像素的百分比在表2显示:
从表2中,可以清晰地看出,在密钥[keyi(i=1,2,...,8)]中细小的差别就可以导致加密图像大的改变。因此,一个好的加密系统必须具有较高的敏感度。
2.5执行时间
一个图像加密算法的执行时间取决于许多因素,如CPU结构,内存大小,操作系统,程序设计语言,编译器选项,编程技巧和代码优化等。当用相同的环境进行了分析比较,会提出了明确的加密方案,用于测量图像密码的速度。
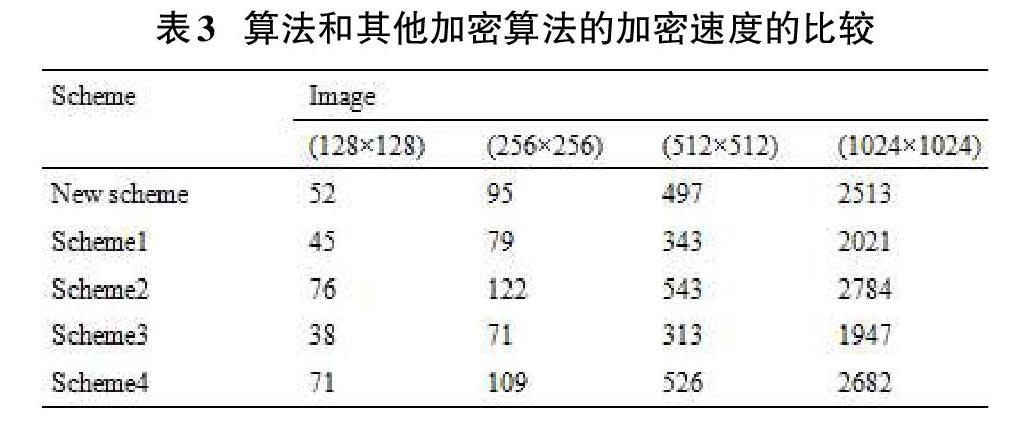
為了更准确地测出加密速度,实现了MATLAB代码的加密算法和其他方案。多次执行每一组的定时测试,测试结果如表3所示。经过该算法和其他加密算法的加密速度的比较,得出该加密算法有着可接受的加密速度的结论。
3总结
针对开放网络环境中存在的数字图像隐私保护这一亟待解决的问题,基于混沌理论提出一种创新、安全、有效的图像加密算法,确保图像安全。在方案设计方面,借助一维混沌映射生成动态S盒,并结合S盒替换、置乱、扩散三种技术设计加密方案。在实验验证方面,分别从密钥空间分析、密钥敏感度分析、直方图分析、相关性分析、明文与密文对比分析、执行时间等方面全面验证所提出加密方案的有效性。
参考文献:
[1] 王雅庆. 基于混沌的数字图像加密算法研究[D]. 重庆大学, 2013.
[2] Wang Y, Wong K W, Liao X, et al. A chaos-based image encryption algorithm with variable control parameters[J]. Chaos Solitons & Fractals, 2009, 41(4):1773-1783.
[3] Wang Y, Wong K W, Liao X, et al. A new chaos-based fast image encryption algorithm[J]. Applied Soft Computing, 2011, 11(1):514-522.
[4] Seyedzadeh S M, Mirzakuchaki S. Image encryption scheme based on Choquet fuzzy integral with pseudo-random keystream generator[J]. 2011.
[5] Zhou Y, Long B, Chen C L P. Image encryption using a new parametric switching chaotic system[J]. Signal Processing, 2013, 93(11):3039-3052.
[6] X. Wang, L. Teng, X. Qin, A novel colour image encryption algorithm based on chaos, Signal Process. 92 (4) (2012) 1101–1108.
[7] X. Wang, L. Liu, Y. Zhang, A novel chaotic block image encryption algorithm based on dynamic random growth technique, Opt. Lasers Eng. 66 (2015) 10–18
[8] Z. Hua, Y. Zhou, C.M. Pun, C.L. Philip Chen, 2D sine logistic modulation map for image encryption, Inf. Sci. 297 (2015) 80–94
[9] X.Y. Wang, L. Yang, R. Liu, A. Kadir, A chaotic image encryption algorithm based on perceptron model, Nonlinear Dyn. 62 (3) (2010) 615–621.
【通联编辑:唐一东】

