数据的正态性检验及Excel/SPSS/Stata 软件的实操应用
陈 军
(新疆师范大学 商学院,新疆 乌鲁木齐 830017)
1 数据正态性检验的相关理论
多数统计检验都要求数据满足正态分布,特别是针对小样本。如果误差项不服从正态性假定,虽然可以利用最小二乘法进行参数估计,但却无法进行检验和预测。如果解释变量不能很好地匹配因变量的峰度和偏度,将会导致样本性质中的统计推断结果发生偏差。实际情形中,出于样本可获得性的考虑,通常采用对数据进行变换的方法,将其数据转换成正态分布,但应该注意到,在数据转换的同时已将数据蕴含的原始信息发生了改变。由此得到的回归结果,其参数的意义解释也已和变换前有所改变。
数据正态性检验的方法主要有两类:使用图形进行大致的判断以及使用统计检验。图形检验中常用的是直方图和正态分位数图。如果得到的数据直方图和钟形相差很大,则拒绝正态性分布,这是一种非常直观的方法,实用性强。使用统计检验多基于卡方统计量,实质是根据下表1 中标注的区间找到落在该区间内的实际观测值个数和期望观测值个数,然后进行卡方检验。
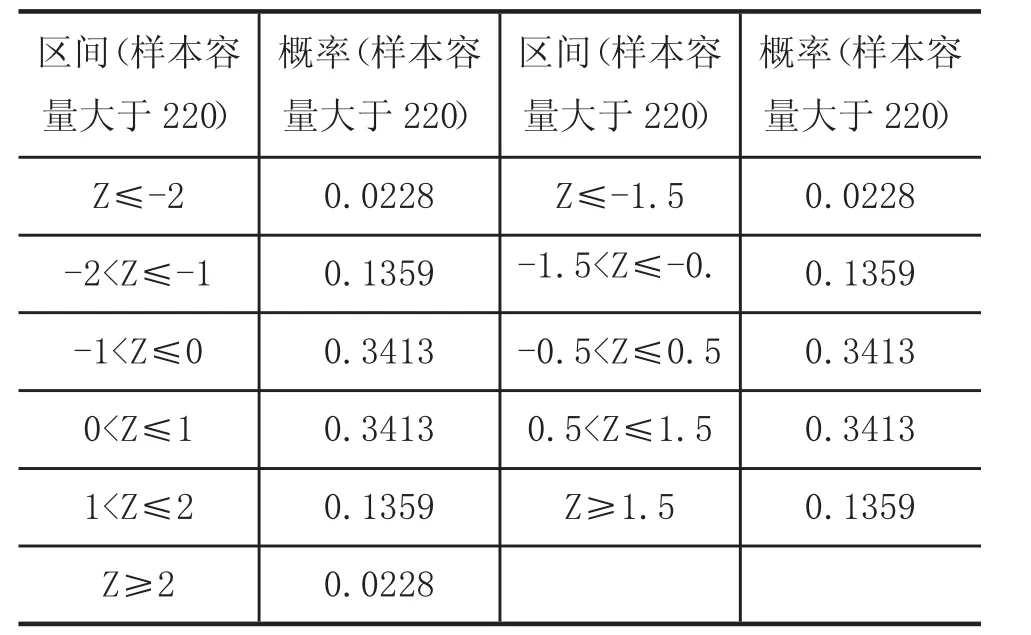
表1 卡方检验区间划分
数据正态性的其他统计检验,包括偏度-峰度检验、D′Agostino 检验、Shapiro-Wilk w 检验和Shapiro-Francia w′检验。应该注意,随着样本量的增大,所有的统计检验趋于拒绝原假设,而图形、偏度及峰度的数值分析可能更有利于研判数据正态性状况。
2 Excel 对于数据正态性的检验
Excel 对于数据正态性的检验方法相对单一,一般采用绘制正态概率图。如果标准正态概率图中的点基本围绕在一条直线周围,那么可以说该组数据基本服从正态分布。下面结合具体的例题进行。
例:某车间加工一批零件尺寸如下表2,请问零件尺寸是否呈正态分布。

表2 车间加工的零件尺寸数据 单位:毫米
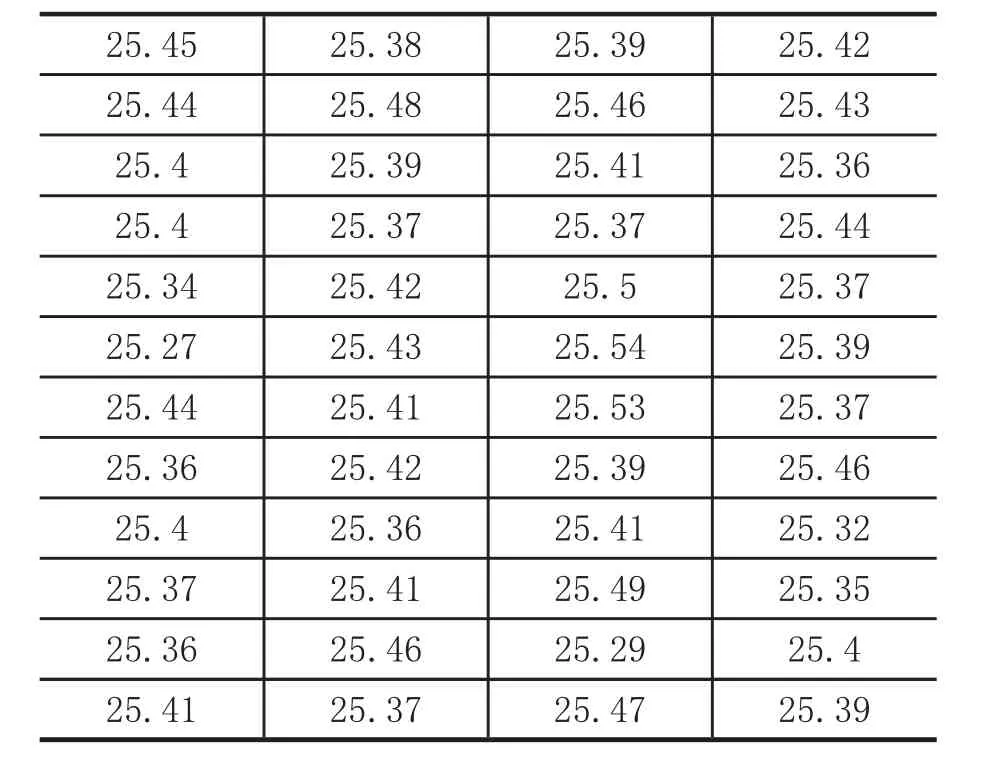
25.45 25.38 25.39 25.42 25.44 25.48 25.46 25.43 25.4 25.39 25.41 25.36 25.4 25.37 25.37 25.44 25.34 25.42 25.5 25.37 25.27 25.43 25.54 25.39 25.44 25.41 25.53 25.37 25.36 25.42 25.39 25.46 25.4 25.36 25.41 25.32 25.37 25.41 25.49 25.35 25.36 25.46 25.29 25.4 25.41 25.37 25.47 25.39
【实验操作步骤】
Step1:将表格数据按照升序排序成一列。
Step2:计算(j-0.5)/100。
Step3:根据(j-0.5)/100=P(Z),求出正态分位数。单击D2 单元格,选择“公式-〉插入函数”。在“插入函数”对话框,“选择类别”选取“统计”,“选择函数”选择“NORM.S.INV”,点击“确定”。结果见下图1。

图1 正态分位数及标准正态分位数计算结果
Step4:,选择“数据-〉数据分析”,在“分析工具”中选择“回归”,单击“确定”。以Zi 为纵轴,X(j)为横轴,绘制标准正态概率图。然后单击“确定”,得到标准正态概率图,如图2 所示。其中,X(j)转化为其对应的百分比排位。可以看出,由(X(j),Zi)形成的点基本围绕在一条直线周围,可以说该组数据基本上服从正态分布。

图2 标准正态概率图
3 SPSS 软件对于数据正态性的检验
SPSS 软件对于数据正态性的检验是建立在数据分布直方图的基础上,可采用多种检验方法。为比较方便,案例数据同上例。
【实验操作步骤】
在SPSS 里执行“分析-〉描述统计-〉频数”(菜单见下图,英文版的可以找到相应位置),然后弹出一个对话框,变量选择左边的“零件尺寸”,再点下面的“图表”按钮,弹出图中右边的对话框,选择“直方图”,并选中“包括正态曲线”。点击“继续”、“确定”按钮。数据分布直方图如下图3。

图3 输出的正态分布图(直方图)
图中横坐标为期零件尺寸,纵坐标为分数出现的频数。从图中可以看出根据直方图绘出的曲线是很像正态分布曲线。如何证明这些数据符合正态分布呢,光看曲线还不够,还需要进一步检验。
(1)检验方法一:看偏度系数和峰度系数
Step1:在“频率”对话框,点击“统计量”按钮,选取如下复选框。点击“继续”、“确定”按钮。选项界面见下图4。

图4 频率:统计量对话框及输出统计量结果
Step2:从“统计量”结果中,看到“偏度”为0.113,“峰度”为0.505,均小于1,可认为近似于正态分布。
(2)检验方法二:单个样本K-S 检验
操作步骤:在SPSS 里执行“分析-〉非参数检验-〉单个样本K-S 检验”,弹出对话框,检验变量选择“零件尺寸”,检验分布选择“常规(正态分布)”,然后点“确定”。结果如下图5。

图5 单样本K-S 检验对话框及输出结果
从结果可以看出,K-S 检验中,Z 值为0.735,P 值(sig 2-tailed)=0.652〉0.05,因此数据呈近似正态分布。
(3)检验方法三:Q-Q 图检验
操作步骤:在SPSS 里执行“分析-〉描述统计-〉Q-Q 图”,弹出对话框,变量选择“零件尺寸”,检验分布选择“正态”,其他选择默认,然后点“确定”,最后可以得到Q-Q 图检验结果,结果很多,我们只需要看最后一个图,见下图6。
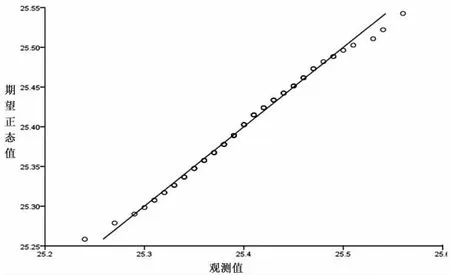
图6 Q-Q 图检验结果(零件尺寸的正态Q-Q 图)
QQ Plot 中,各点近似围绕着直线,说明数据呈近似正态分布。
4 Stata 软件对于数据正态性的检验
Stata 软件对于数据正态性的检验方法主要有分位正态图、正态性统计检验。为比较方便,案例数据同上例。
(1)检验方法一:分位正态图
分位正态图的绘制命令格式如下:Qnorm varname[if][in][,options]
该命令的大部分选项都是绘图命令所共有,独有选项是grid,加入grid 项可以在图中依次标 注 0.05、0.10、0.25、0.50、0.75、0.90、0.95百分位的坐标刻度。分位正态图将观测变量分布的分位数与一个具有相同平均数和标准差的理论正态分布的分位数进行比较,通过比较偏离程度进行直观研判正态性状况。
Step1:打开数据文件。
Step2:在“command”区域输入如下命令:.qnorm size,grid
回车,执行结果如下:

图7 size 的分位正态图
与完全正态分布相比(图中对角线),数据分布近似呈现正态性。
(2)检验方法二:正态性统计检验
【实验操作步骤】
Step1:打开数据文件。
Step2:在“command”区域输入如下命令:sktest size
回车,执行结果如下:

结果显示峰度、偏度检验以及峰度-偏度合并检验都表明呈现正态性(P 大于0.05)。
Step3:在“command”区域输入如下命令:lnskew0 size2=size回车,执行结果如下:

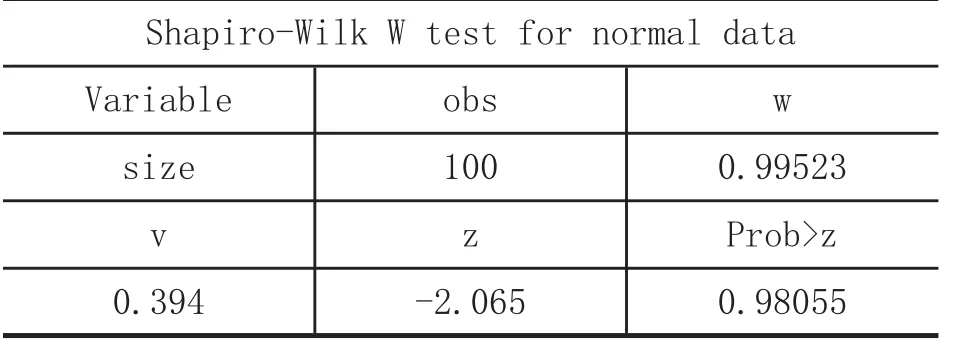
Step4:在“command”区域输入如下命令:.swilk size
回车,执行结果如下:
Step5:在“command”区域输入如下命令:swilk size2,lnnormal
回车,执行结果如下:
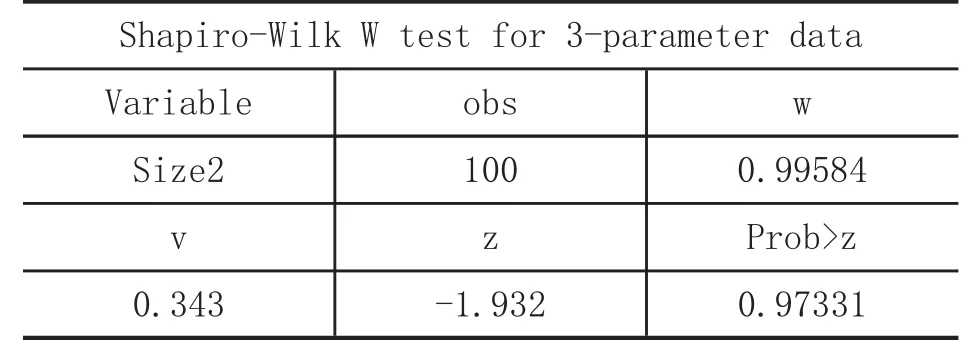
结果显示,同sktest 检验结果一样,表明数据分布呈现正态性。需要说明的是,lnskew0 命令是为变量size 找一个k 使得ln(size-k)的偏度为0,并定义这个新的变量为size2;当对完成这一变换的变量进行swilk 检验时,需要加入lnnormal 选项。
Step6:在“command”区域输入如下命令:.sfrancia size
回车,执行结果如下:

结果显示,同sktest 及swilk 检验结果一样,表明数据分布呈现正态性。
5 结语
通过上文分析,可以看到Excel、SPSS、Stata 几种软件都能处理数据正态性检验,但在具体的应用操作上存在一定差异:Excel 相对简单;SPSS 软件在分布直方图基础上检验方法较多;Stata 软件的检验方法则更为灵活。在实际应用中,要结合数据分析对于总体正态性的要求,像方差分析就要求数据分布满足正态性的条件,而回归分析(特别是大样本)则对于正态性检验的要求就没有那么重要。

