多次地震动作用下对桥梁圆端空心墩的位移响应研究
,2
(1.昆明理工大学 土木工程系,昆明 650093; 2.云南博航交通科技有限公司,昆明 650000)
1 引言
随着国内抗震规范的修订,基于结构性能的抗震设计理念也越来越深入人心[1-3]。相关资料[4-6]表明,由于区域、地质结构、应力场强度等方面的不同,在地震类型中,主余震型占60%,震群型占25%,孤立型地震序列仅占15%。整体上,结构在使用期间遭遇的地震动次数往往较多。有工程实例表明,个别结构在主震中并未发生倒塌现象,却在随后的余震中损坏[7-8]。因此,有很多学者致力于研究多次地震动作用对结构的影响,如:Mhin[9]在上世纪80年代,通过研究非线性单自由度体系对主余震的响应情况,认为主余震要求结构有更高的延性性能; Amadio.C等[10]学者同样通过单自由度体系来研究多次地震动下的结构损伤情况,认为多次地震会加剧结构的损伤; Sunasaka[11]等学者对城市高架桥进行研究,认为后续地震会加剧结构损伤,进而导致结构破坏。
国内方面,张沛洲、康谨之等[12]学者以单自由度为例分析主余震对结构累积损伤及抗震性能的影响; 于晓辉、吕大刚等[13]学者通过对比计算结构在考虑与不考虑多次地震动下的损伤差值,来研究其对结构的损伤影响; 李洪泉等[14]学者通过试验研究分析结构在地震作用下的累计损伤情况; 张煜敏[15]等学者以连续梁为例研究多次地震序列对桥梁结构产生的潜在震害。
以上学者研究均表明,在多次地震作用下,桥梁结构响应往往更为剧烈,导致的损伤也随之增加,在主震作用下未倒塌的结构在随后的余震中存在倒塌风险。但以上研究内容多数以单自由度为主,较少涉及多自由度结构,对山区铁路桥墩常用结构形式圆端空心墩也并未提及,再综合现行铁路抗震设计规范[16]并未考虑多次地震动(不同于频遇地震动)这一现象对桥梁结构的影响,作者以秋末河大桥为工程背景,基于抗震分析软件OpenSees对铁路圆端空心墩进行传统及累计增量动力分析(IDA),对比同一结构在单一地震及多次地震动下位移响应情况,来研究多次地震对铁路空心高墩的位移影响规律,进而给出相关抗震分析计算建议[17]。
2 工程概况
秋末河大桥位于成都至兰州铁路路段内,为一段曲线梁桥,前连成都,后接兰州,其复杂的水文地质条件给设计及施工带来诸多不便。大桥分左右两线桥,左线桥总长751.6m,右线桥总长743.5m,由24m及32m装配式预应力混凝土T梁桥组成,施工方法为先简支后连续,结构总体图如图1所示。该桥桥墩普遍较高,在30.5m到42.5m之间,设计时采用变截面圆端形式,外部变化比例为40∶1,内部空心部分变化比例为70∶1,桥墩上下两端部为变截面圆端实心墩,端部位置设置倒角,桥墩大样如图2所示,主要截面大样如图3所示。
3 模型建立
3.1 Midas全桥及单墩模型
采用桥梁通过有限元软件Midas/civil建立秋末河大桥全桥有限元模型,如图4所示。上部主梁采用梁单元模拟,下部桥墩、桩基础同样采用梁单元进行模拟,其中,桩—土相互作用通过在桩基础上施加等效节点弹簧来模拟,弹簧刚度采用“m”法进行计算。
由于秋末河大桥桥墩截面形式相同,均为变截面圆端桥墩,全桥模型分析计算较为繁琐,为提高计算效率,取一个具有代表性的桥墩进行研究,所选取的桥墩设计参数如表1所示。通过全桥有限元模型计算出主梁作用于单墩墩顶的竖向力,随后建立Midas/civil单墩有限元模型,计算其动力特性,顺桥向振型如图5所示,顺桥向振型参与质量如表2所示,累积质量参与系数随振型变化情况如图6所示。
从表2中可以看出,单墩第一阶振型质量参与质量较小,从图6的变化情况来看,当顺桥向累积质量参与系数达到90%以上时,振型数量为17,结合图5所示内容,发现其高阶振型较为明显,该圆端空心墩结构较柔,刚度相对较小,和以往研究的低阶振型为主的结构有所不同。

图1 秋末河大桥Fig 1 Qiumohe bridge

图2 桥墩构造Fig 2 Pier structure
图3 桥墩横截面Fig 3 Pier cross-sections

图4 Midas/civil有限元模型Fig 4 Midas/civil finite element model
表1 结构设计参数
Table 1 Structural design parameters

混凝土材料钢筋材料高度(m)截面尺寸(m)剪跨比轴压比墩身纵筋配筋率高配筋区低配筋区箍筋间距配箍率箍筋间距配箍率C35HRB40034.407.0×5.26.630.031.21%10 cm0.91%15 cm0.65%

图5 桥墩纵桥向部分振型Fig 5 Partial longitudinal mode of the pier
表2 顺桥向周期及参与质量
Table 2 Longitudinal period and participation mass

模态号周期/s振型参与质量/%10.354839.3030.073916.4360.03137.2080.01864.31110.01313.48130.01023.83
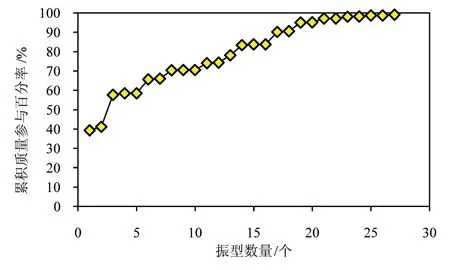
图6 累积质量参与系数分布Fig 6 Cumulative mass participation coefficient distribution

图7 混凝土本构曲线Fig 7 Concrete constitutive curve
3.2 OpenSees单墩模型
由于OpenSees处理抗震过程中涉及到的非线性能力较强,因而广泛应用于结构抗震分析中。本次模拟内容包括以下几方面:材料的本构关系、单元类型的选取、结构单元的离散、结果输出。模型参数见表1所示,本模型所涉及材料为钢筋和混凝土。对于钢筋采用OpenSees中自带的Steel01理想弹塑性材料; 对于混凝土材料,将其分为强约束区、弱约束区与非约束区,分别采取不同参数、相同本构类型的Concrete02材料进行模拟,其本构曲线如图7所示。由于本桥墩高阶振型较为明显,因此桥墩单元数量取为30。建立单墩结构后,将全桥模型中计算出的竖向力作用于单墩墩顶,并将其转化为质量进行数值模拟。
3.3 地震波的选取
当地地质资料表明,秋末河大桥地震动反应谱特征周期为0.45s,结合本文所研究内容为多次地震作用对铁路圆端空心墩的位移响应影响规律,所选取地震波均为实际记录地震波,具体如图8-10所示。
4 计算分析
4.1 累积增量动力分析

图8 El Centr地震波 图9 唐山迁安地震波Fig 8 El Centr earthquake wave Fig 9 Tangshan Qian'an earthquake wave
图10 汶川绵竹地震波 图11 累积增量动力分析加载方式Fig 10 Wenchuan Mianzhu earthquake wave Fig 11 Cumulative IDA loading mathod
传统增量动力分析(IDA)[18]是指,对结构作用一系列相同变化规律、不同峰值加速度的地震动,通过分析结构的响应变化规律,来研究结构的抗震性能,通常选用某个特定的指标进行评价,如位移延性、曲率延性、位移角等。该方法首先由Bertero[19]提出,随后被美国相关规范所采纳[20-21],该方法发展至今,已逐渐被人们作为一种评价结构整体抗侧倾能力的常用手段。
表3 El Centro地震波作用下结构位移
Table 3 Structural displacement with El Centr earthquake wave

0.1g0.2g0.3g0.4g0.5g0.6g0.7g0.8g最大正向位移32.5863.0896.12148.31187.01194.41193.31215.52最大负向位移-28.35-61.79-97.28-150.18-197.21-226.12-252.02-276.43绝对最大位移32.5863.0897.28150.18197.21226.12252.02276.43残余位移-1.08-2.01-3.25-5.68-8.15-9.54-10.00-13.86

表4 唐山迁安地震波作用下结构位移Table 4 Structural displacement with Tangshan Qian'an earthquake wave
虽然该方法被广泛接受,但其对考虑结构在多次地震动下的响应情况尚有欠缺。基于上述不足,作者提出累积增量动力分析方法,来考虑结构在多次地震动下的响应。具体加载方式如图11所示,在同一次分析工况中,同时作用一系列相同规律、不同峰值的地震动,为了使结构充分振动,经试算后,在每个地震动后增加30s的间隔期。
4.2 计算结果
结构在传统增量动力分析下的位移情况在后续对比数据中给出; 结构在累积增量动力分析下的位移时程曲线如图12-14所示。将同一地震波下不同分析方法得到的位移结果进行对比,如图15-17所示,两种分析方法作用下,绝对最大位移比值、残余位移比值情况见表3-5所示。
4.3 结果分析
从传统IDA计算结果上看,结构绝对最大位移及残余位移随着峰值加速度的增加而增加,其原因较为明显,对于最大位移响应而言,地震波加速度增加,结构的惯性力也随之增加,结构最大位移响应也随之增加; 对于残余位移而言,其变化情况需分两种情况分析:当结构处于弹性范围内时,残余位移随着加速度变大而变大,可认为近似为现象增加,当结构处于弹塑性范围内时,残余位移随着加速度的变大而变大,且速度较弹性明显,其原因在于结构进入弹塑性后,结构会产生相应新的塑性位移;

图12 El Centro地震波累积IDA结果 图13 唐山迁安地震波累积IDA结果Fig 12 Cumulative IDA result of El Centr earthquake wave Fig 13 Cumulative IDA result of Tangshan Qian'an earthquake wave

图14 汶川绵竹地震波累积IDA结果图 图15 位移对比—El Centro Fig 14 Cumulative IDA result of Wenchuan Mianzhu earthquake wave Fig 15 Displacement comparison—El Centro
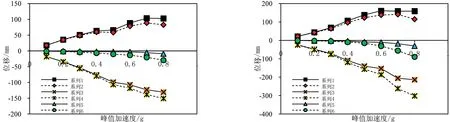
图16 位移对比—唐山迁安 图17 位移对比—汶川绵竹Fig 16 Displacement comparison—Tangshan Qian'an Fig 17 Displacement comparison—Wenchuan Mianzhu
表5 汶川绵竹地震波作用下结构位移
Table 5 Structural displacement with Wenchuan Mianzhu earthquake wave

0.1g0.2g0.3g0.4g0.5g0.6g0.7g0.8g最大正向位移21.9644.1068.95106.36138.51160.91158.53158.60最大负向位移-24.15-48.03-71.17-109.53-140.17-153.36-205.99-213.56绝对最大位移24.1548.0371.17109.53140.17160.91205.99213.56残余位移-0.57-1.98-2.05-4.29-8.57-10.57-18.49-30.11
表6 结构位移对比—El Centro
Table 6 Structural displacement comparison—El Centro

传统分析最大位移/mm32.5863.0897.28150.18197.21226.12252.02276.43残余位移/mm-1.08-2.01-3.25-5.68-8.15-9.54-10.00-13.86累积分析最大位移/mm32.5865.79105.31165.61224.04260.11297.00336.43残余位移/mm-1.08-4.00-8.02-15.17-24.42-34.59-45.62-61.64累积/传统最大位移11.041.081.101.141.151.181.22累积/传统残余位移11.992.472.673.003.634.564.45
表7 结构位移对比—唐山迁安
Table 7 Structural displacement comparison—Tangshan Qian'an

传统分析最大位移/mm18.0735.8853.6976.0499.19107.51123.25130.65残余位移/mm-.071-1.38-2.14-2.60-2.81-3.13-5.77-8.94累积分析最大位移/mm18.0734.9555.8179.59106.70118.04138.16150.72残余位移/mm-0.71-1.88-4.27-6.80-10.32-13.36-20.68-29.01累积/传统最大位移10.971.041.051.081.101.121.15累积/传统残余位移11.371.992.613.684.263.593.25
表8 结构位移对比—汶川绵竹
Table 8 Structural displacement comparison—Wenchuan Mianzhu

传统分析最大位移/mm24.1548.0371.17109.53140.17160.91205.99213.56残余位移/mm-0.57-1.98-2.05-4.29-8.57-10.57-18.49-30.11累积分析最大位移/mm24.1550.6376.07119.39156.16185.99261.97301.24残余位移/mm-0.57-2.54-4.81-9.26-14.86-30.86-55.86-89.52累积/传统最大位移11.051.071.091.111.161.271.41累积/传统残余位移11.282.352.161.732.923.022.97
从累积IDA计算结果上看,结构绝对最大位移及残余位移同样随着峰值加速度的增加而增加。原因大致同上,但同时又稍有不同。对于累积分析,结构的最大位移及残余位移较传统分析更大,其原因为:在进行累积IDA计算时,较高地震波工况的开始状态为较低地震波工况的结束状态,继承了上一工况后的结构状态。若上一工况结束状态存在残余位移,则下一工况的残余位移会更大; 若上一工况结束时存在损伤、材料刚度退化等不利结构受力的状态,则下一工况也会完全继承,导致结构会发生更大的损伤、材料刚度进一步退化等现象,故而结构的位移响应会更大。
将两种分析方法再次进行对比,从计算对比图(图15至图17)、对比表(表3至表5)所示内容,可以发现,累积IDA作用下的结构位移响应存在“跑偏”现象,即位移向某一方向增加; 同时,对于结构最大位移响应而言,当结构处于弹性状态,其最大位移响应的误差在5%以内,在工程可接受误差范围内; 当结构处于弹塑性状态,最大位移响应差异较大。对于结构残余位移而言,无论结构处于弹性还是弹塑性状态,其差异均很大,不容忽视。
通过以上对比分析可知,多次地震动对铁路圆端空心墩的位移响应有较大的影响,主要原因在于前一地震工况产生的结构刚度退化、材料损伤及残余位移对后一地震工况有较大的影响。本文涉及的是圆端空心墩,结构高阶振型较为明显,不再是低阶振型控制结构响应的结构,希望以后再进行相关结构的抗震位移性能分析时,能够参考本文的相关分析结果。
5 结论
(1)本文以秋末河大桥为工程背景,通过Midas/civil建立全桥模型计算后简化出单墩模型,通过OpenSees对圆端空心墩进行地震作用下位移性能分析;
(2)该圆端空心墩结构较柔,高阶振型较为明显,并非低阶振型控制的结构,在进行单一地震动计算时,即进行传统IDA,结构最大位移及残余位移随峰值加速度的增加而增加;
(3)在考虑多次地震动对结构影响情况下,即进行累计IDA计算,结构的位移响应与不考虑该影响时位移响应有较大区别,当结构处于弹性时,最大位移响应差异不大,误差在5%以内,为工程可接受误差; 当结构处于弹塑性时,最大位移响应差异较大,不可忽略; 且随着弹塑性的发展,多次地震动对最大位移的影响也更为明显;
(4)多次地震动对圆端空心墩结构的残余位移影响很大,即使结构处于弹性状态,其差异也较大,不容忽视; 随着结构弹塑性的发展,多次地震动对其影响(即两种情况下的残余位移比值)也趋于稳定。

