基于萤火虫算法的最大值最小化着色旅行商问题的求解
王东明, 代 星, 孟祥虎, 徐向平, 李 俊
(东南大学复杂工程系统测量与控制教育部重点实验室, 南京 210096)
0 引言
多旅行商问题(multiple traveling salesman problem, MTSP)是一种典型的组合优化问题, 近年来, MTSP已被成功应用于各类优化调度问题.着色旅行商问题(colored traveling salesman problem, CTSP)通过引入颜色来区分城市对旅行商多样的可访问性, 解决了MTSP难以描述城市可访问性差别的难题[1].本课题组提出的CTSP[2-4]及相关的应用研究[5-6]均以各旅行商的路径总和最小化为目标, 而未考虑各旅行商间旅行结果路径的差异,导致整个系统的效率下降.最大值最小化着色旅行商问题(min-max colored traveling salesman problem, MM-CTSP)采用最大旅行商路径最小化的目标代替总路径最小化的目标,有望一定程度地均衡各旅行商之间的旅行结果路径差异,从而提高系统的运行效率[7].遗传算法(genetic algorithm, GA)能成功求解着色旅行商问题, 但当城市规模增加时,该算法的耗时急剧增加且解质量变差[7].王艳[8]提出改进的离散化萤火虫算法(firefly algorithm, FA)求解旅行商问题,并证明了FA的收敛速度优于GA.Sayadi等[9]将FA算法应用到车间作业调度中,验证了FA算法的求解结果优于蚁群算法.于宏涛等[10]提出一种结合变邻域搜索算法思想的离散人工萤火虫算法求解旅行商问题, 并验证了该算法的有效性.本文拟采用FA来求解MM-CTSP, 以均衡各旅行商间的行程, 并通过仿真实验检验该方案的性能.
1 MM-CTSP模型
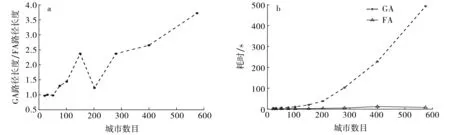
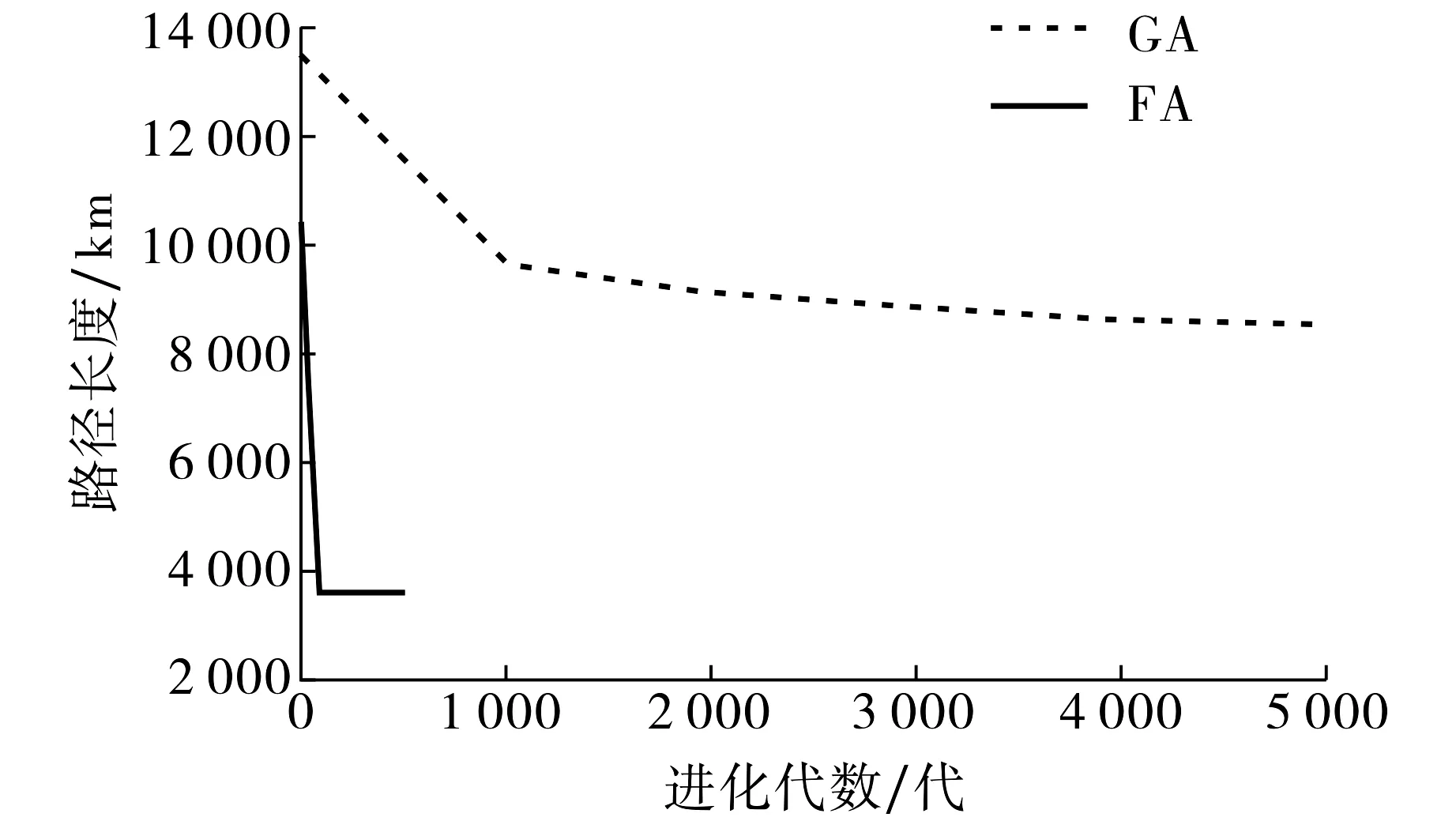
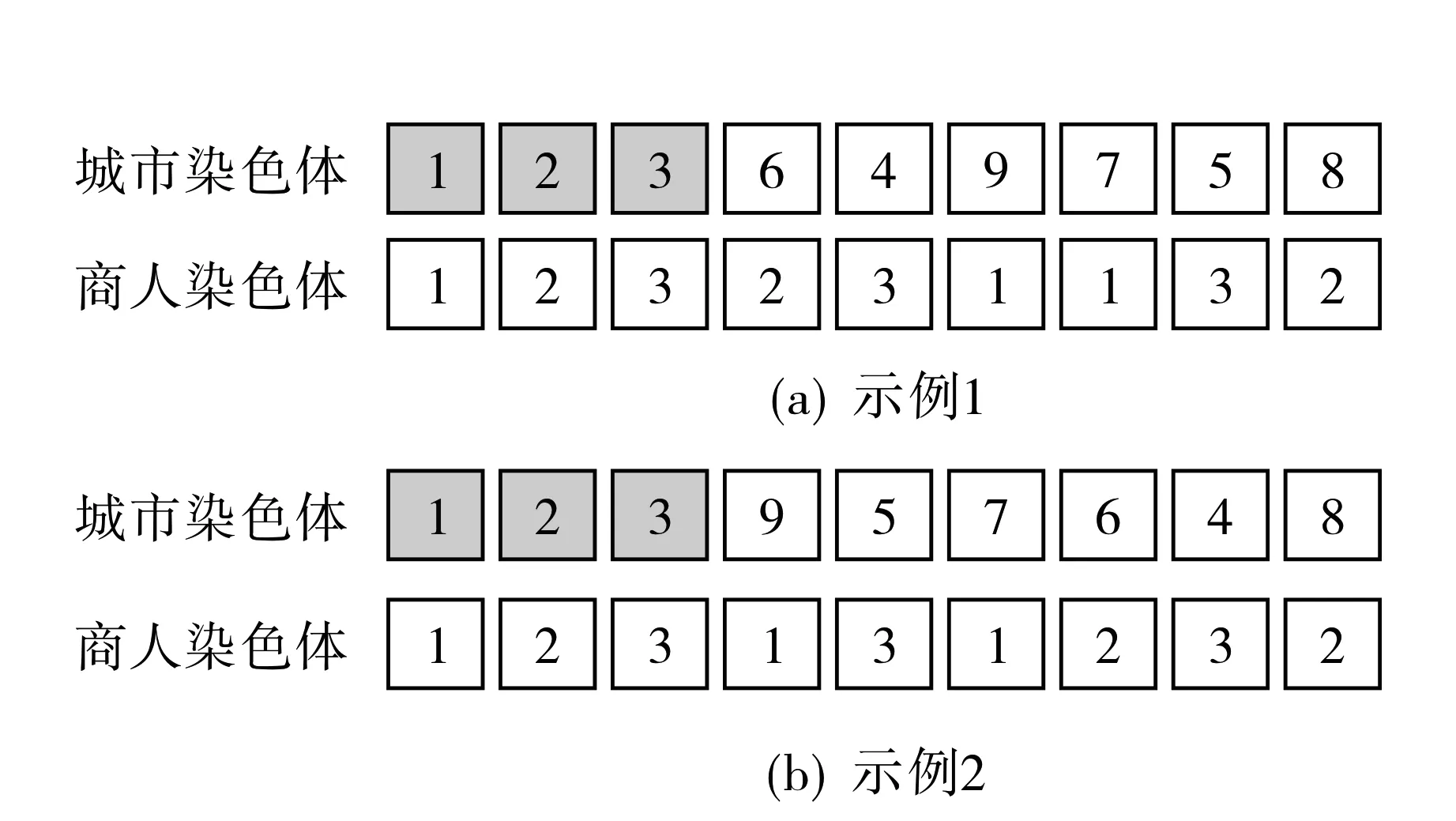
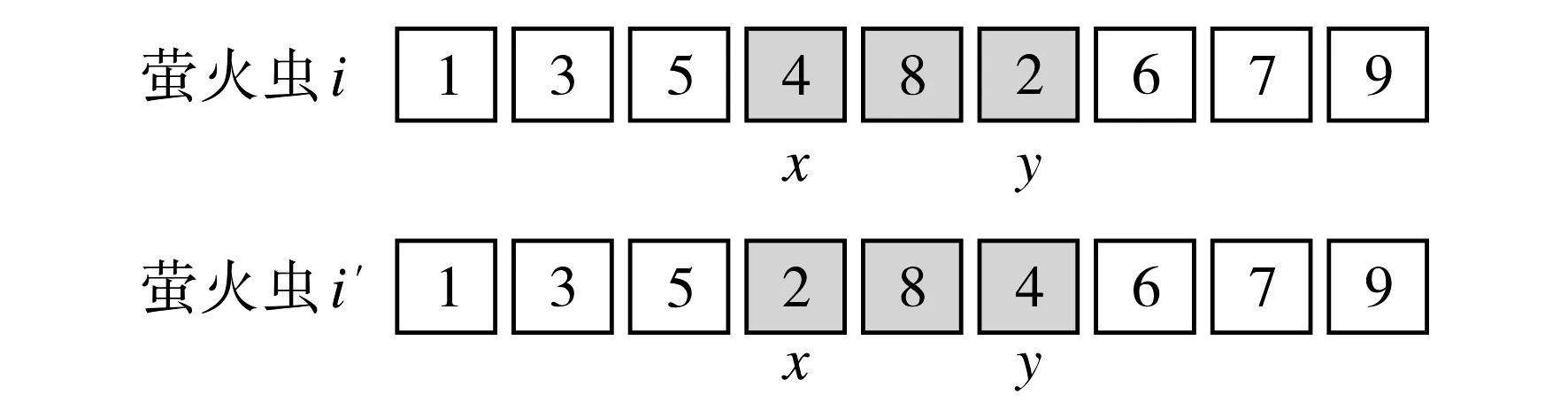
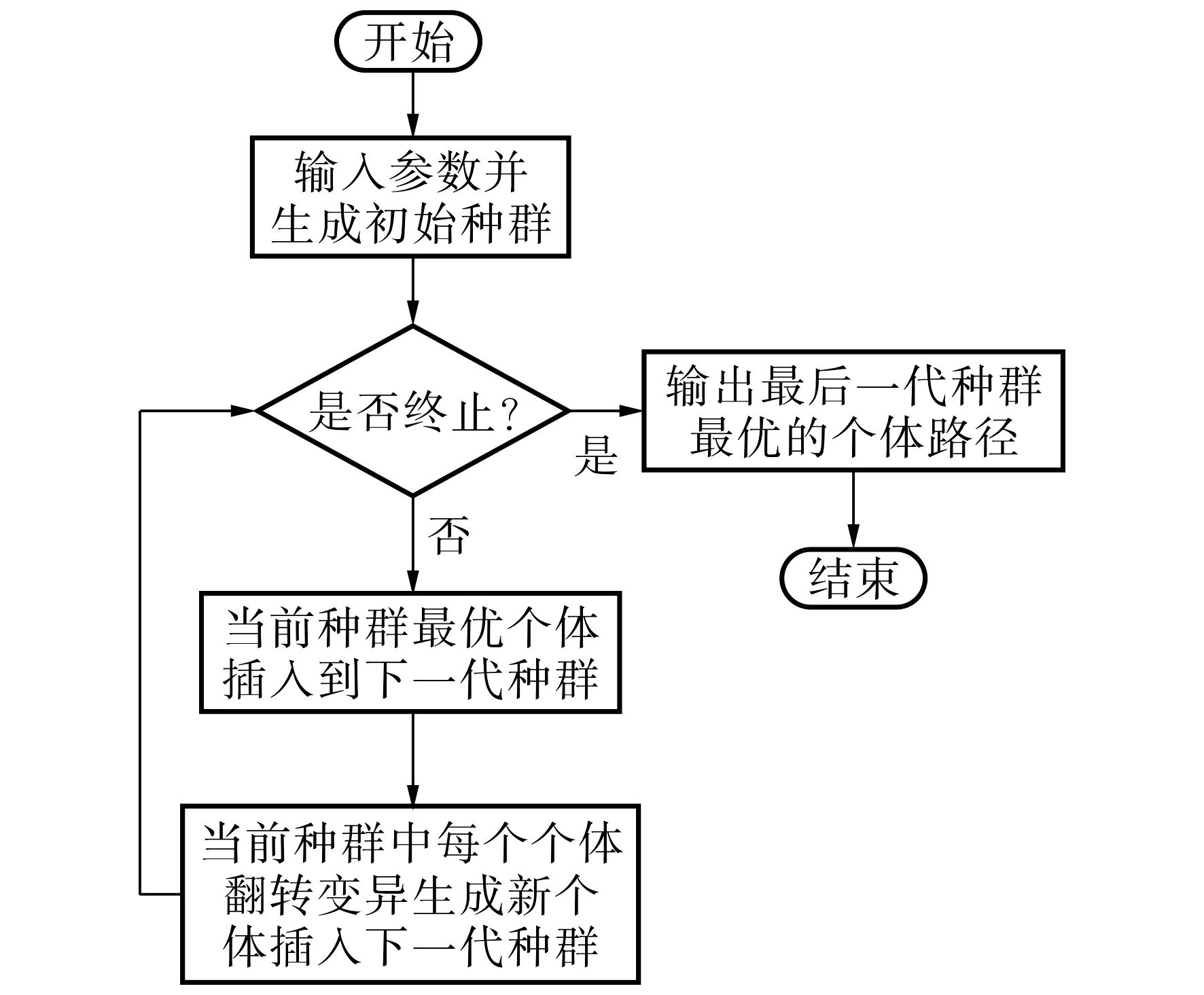
假设有m个商人和n个城市,m MM-CTSP的目标是将最大旅行商的花费最小化, 其目标函数为 (1) 1) 所有商人的起始城市和终止城市是商人各自的起始城市: ∑ixdkik=1, ∑ixidkk=1, ∀i∈Ik{dk}, ∀k∈Z; (2) 2) 商人k不能访问不含颜色ck的城市: ∑i∑jxijk=0, ∑i∑jxjik=0, ∀i∈V,∀j∈VIk,∀k∈Z; (3) 3) 所有城市被访问的次数为1: ∑i∑kxijk=1, ∑i∑kxjik=1,j≠i,∀i,j∈Ik,∀k∈Z; (4) 4) 所有城市只能被一个商人访问一次,即城市i被商人k访问: ∑jxjik=∑lxilk,i≠j≠l,∀j,i,l∈V; (5) 5) 去除无效的子环: uik-ujk+nxijk≤n-1,j≠i, ∀i,j∈Ik{dk}, ∀k∈Z, (6) 其中uik表示商人k的路径中从起始城市dk到城市i的城市个数. 目标函数(1)及约束方程(2)~(6)构成MM-CTSP模型.由于通用CTSP已被证明是NP-hard问题[4],而在此基础上提出的MM-CTSP依然是NP-hard问题,其精确求解很困难,故本文采用智能算法求解MM-CTSP. 图1 双染色体编码Fig.1 Dual-chromosome coding 采用双染色体编码[1]对CTSP进行编码, 城市染色体描述城市编号序列,商人染色体描述访问对应城市编号的商人编号.图1给出了CTSP双染色体编码的2个示例, 其中城市染色体中前面3个节点是每个商人所对应的起始城市, 在每个商人路径后须加入对应的起始城市.由图1可见, 示例1,2中商人1的路径为1-9-7-1, 商人2的路径为2-6-8-2, 商人3的路径为3-5-4-3.双染色体编码对不同的基因链解码后得到的路径可能相同,并且在执行两条基因编码的交叉和变异操作后须重新确认城市编码基因与旅行商编码基因间对应关系的正确性, 故编码方案耗时长,效率较低[2]. 直接路径编码中所有商人都有一个城市访问序列, 如图2所示,在每个商人的城市访问序列后加上商人各自的起始城市即得到商人1的路径为1-9-7-1, 商人2的路径为2-6-8-2, 商人3的路径为3-5-4-3.由于直接路径的编码与解码一一对应, 故本文采用直接路径编码. 适应度函数F=1/(1+fmax),fmax=max(f1,f2,…,fm), 其中fmax表示最大的旅行商路径值,fi表示商人i的路径值,i∈Z. 适应度值F越大表明解质量越好, 同时F也代表了萤火虫的亮度. 萤火虫之间的距离r=10d/n, 其中d为2个萤火虫路径存在差异边的数目,n为城市的数目. 距离为r的2个萤火虫之间的吸引力β(r)=β0e-γr2,β0是其中较亮的萤火虫的亮度值,γ为光强吸收系数. 当萤火虫i的亮度值小于萤火虫j对萤火虫i的吸引力值时, 萤火虫i通过定点翻转变异更新, 否则采取随机翻转变异. 图3 翻转变异Fig.3 Inversion mutation 翻转萤火虫i路径中点x,y之间的路径生成新的引火虫i′, 如图3所示.定点翻转变异是通过存在的不同边找到定点x,y并翻转变异更新.随机翻转变异则随机选取不相等的x,y进行翻转变异更新.比较萤火虫i和萤火虫i′的亮度, 保留亮度大的萤火虫. 图4 FA算法流程示意图Fig.4 Flow chart of FA FA的算法流程如图4所示.首先随机初始化第一代萤火虫种群,将当代种群中最亮的萤火虫保留到下一代种群,然后对当代种群的所有萤火虫进行翻转变异更新,并将更新后的萤火虫插入到下一代种群,直至达终止条件时最后一代种群中最亮萤火虫的最大商人路径即算法所得解. 为了验证萤火虫算法求解MM-CTSP的性能, 设计10个案例分别从解质量、耗时和收敛速度等3个方面对FA与GA进行分析. 本文案例中所有数据的坐标来自TSPLIB问题库.实验平台是安装有32位Windows7操作系统的Dell Optiolex3020, CPU为Inter Core i3, 主频3.4 GHz, 4 GB内存.算法程序采用C++实现, 运行平台为VS2013.所有案例中的城市坐标和城市颜色分配文件来源于https://pan.baidu.com/s/10hV2u5cdGLqTiFGh0Gd0fQ. 每个算法的种群个体设置为20, 各算法在达到105次函数评价时停止迭代更新, FA的光强吸收系数γ取0.06.所有案例运行算法10次, 取运行结果得到最大商人路径的最优解、最差解和平均值, 结果如表1及图5所示.由表1和图5可知,在案例1~3中, GA和FA的解质量相近, FA的耗时远小于GA; 在案例4~10中, FA的解质量和耗时都优于GA, 且随着城市规模的增大, FA的解质量和耗时的优势更明显. 表1 GA与FA求解MM-CTSP的实验结果 图5 平均解质量(a)及耗时(b)随城市数目变化的关系曲线 Fig.5 Average solution quality and time consuming 图6 案例6的进化曲线Fig.6 Evolutionary curve of case 6 图6给出了2种算法在案例6中每代种群中最好个体的进化曲线.由图7可知, 在105次函数评价下, FA的迭代次数仅为500代, GA的迭代次数为5 000代, 但是当FA迭代到约100代时即已收敛且解质量优于GA. 综上所述, 当求解MM-CTSP的城市规模小于76个时, GA与FA的解质量接近, 但FA的耗时较少;当城市规模大于76个时, FA的解质量优于GA, 且耗时少, 收敛速度快,随着城市规模的进一步增加,FA在解质量和耗时上的优势更明显.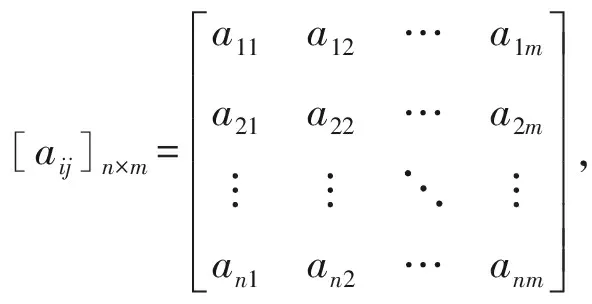
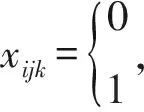
2 萤火虫算法
2.1 编码设计
2.2 亮度与距离
2.3 吸引力与萤火虫更新
3 实验结果与分析