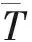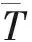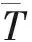外逆的扰动与最简表示
张慧淳, 潘维维, 郭志荣, 黄强联*
(1. 扬州大学数学科学学院, 江苏 扬州 225002; 2. 扬州职业大学数学学院, 江苏 扬州 225009)
一些重要的广义逆, 如Moore-Penrose逆[1-2]、 Drazin逆[3]和群逆[3-4]都是外逆, 由于非零有界线性算子总存在非零外逆, 同时外逆具有一定的稳定性, 因而外逆广泛应用于数值分析[1-2]、算子方程[5]、最优化和数理统计[2]等学科中.Nashed[6]首先研究了外逆的扰动, 给出了外逆稳定性定理; Wei[7]研究并总结了外逆的扰动与表示; Huang等[8]讨论了外逆的稳定扰动与最简表示, 得到了最简表示为广义逆、Moore-Penrose逆、Drazin逆和群逆的特征; Zhu等[9]在仅假设外逆的条件下给出了最简表示为广义逆、Moore-Penrose逆、Drazin逆和群逆的充要条件.本文拟在文献[9]的基础上探讨最简表示为扰动算子的{2,3}-逆、{2,4}-逆和{2,5}-逆的充要条件, 并对文献[8-10]的相关结果进行推广、改进与补充.
1 预备知识

设非空集合θ⊆{1,2,3,4,5}, 算子S∈B(Y,X), 方程: (1)TST=T; (2)STS=S; (3) (TS)*=TS; (4) (ST)*=ST; (5)TS=ST, 其中T*表示T的共轭算子.若算子S满足方程(i) (∀i∈θ), 则称S为T的θ-逆, 记为Tθ.每种θ-逆都有其自身的性质和意义, 如{1}-逆为内逆; {2}-逆为外逆;{1,2}-逆为广义逆, 记为T+;{1,2,3,4}-逆为Moore-Penrose逆, 记为T†; 而{1,2,5}-逆则为群逆, 记为T#.




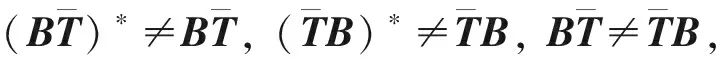
引理4[10]设X=M1⨁N=M2⨁N, 若M1⊆M2, 则M1=M2.
2 主要结果

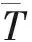
若定理5中的条件外逆T{2}为T的{2,3}-逆T{2,3}, 则可得到如下结果.

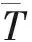

注7推论6改进了文献[8]的定理2.4, 后者仅证明了1)与3)等价.

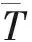

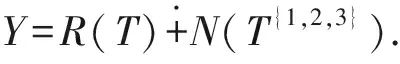
类似可得下列结论.