亚纯双单叶函数类的系数不等式
2019-08-12 03:12李小飞冯建中
扬州大学学报(自然科学版) 2019年2期
秦 川, 李小飞, 冯建中*
(长江大学 a. 工程技术学院; b. 信息与数学学院, 湖北 荆州 434022)
设Ω表示圆盘外区域V={z∈C, 1<|z|<+∞}内具有形式为
(1)
的亚纯单叶函数族, Bulut[1]定义了一类V内的亚纯函数类Ωs(β,λ), 亚纯函数和亚纯双函数及其子类的性质已有不少研究, 亚纯函数理论被应用在单复变各个领域,如唯一性理论、值分布理论、复微分及差分方程理论、正规族理论等,其研究领域逐步深入至多复变理论.通过解析函数理论和不等式理论,文献[2-4]利用一类线性算子定义了一类亚纯函数族的卷积性质; 文献[5-7]引入了具有复数阶,并利用线性算子定义了一类亚纯单叶函数类,研究了它的系数估计; 文献[8-9]通过引入三阶微分算子和乘积变换, 研究了一类亚纯单叶函数族的包含性质、幅角性质和从属性质.本文拟构造一类亚纯单叶函数族和一类亚纯双单叶函数族,利用微分从属的性质研究系数的上限估计, 并由此推导出Fekete-Szegö不等式, 从而推广了亚纯函数类的系数估计,丰富了微分从属的理论.
1 预备知识
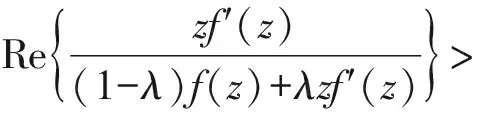
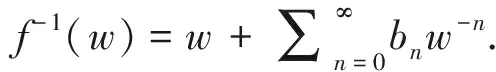
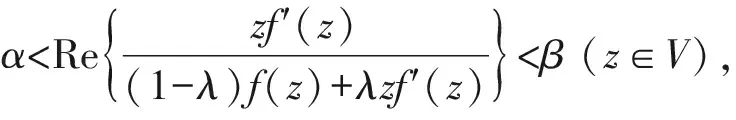
定义3若g=f-1, 且f,g∈Ωs(α,β,λ), 则称f为亚纯双单叶函数,记为f∈Ωs,σ(α,β,λ).
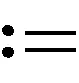
2 主要结论
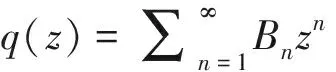
引理2[11]设α,β为实数且满足0≤α<1<β,定义p(z)=1+iπ-1(β-α)log([1-zexp(2πi·(1-α)/(β-α))]/(1-z)), 则p(z)将单位圆盘U映射为带状区域{w:α 引理4[13]若函数p(z)=1+p1z+p2z2+…在U内解析,且具有正实部,则对任意k=1,2,…,都有|pk|≤2. P1h1/2=-(1-λ)a0,P1k1/2=(1-λ)a0, (2) (3)
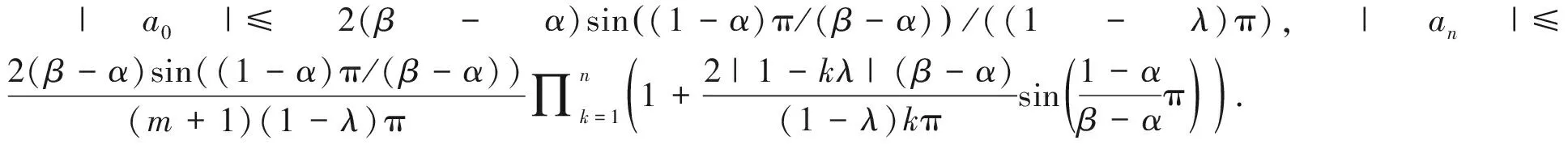
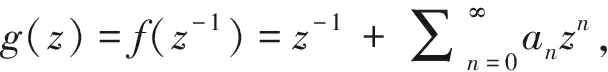
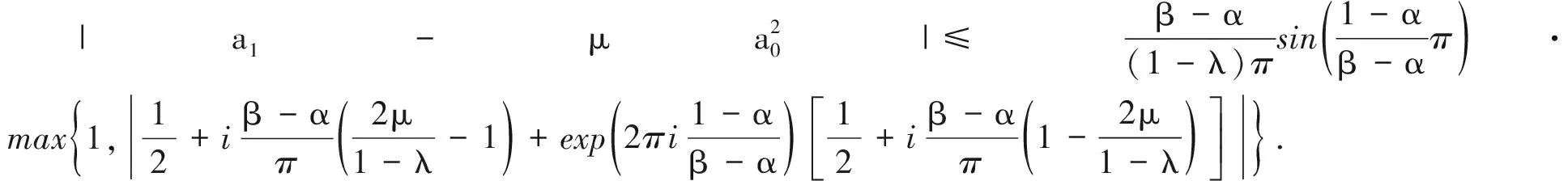

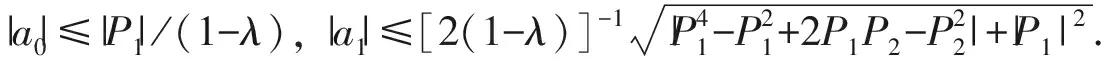
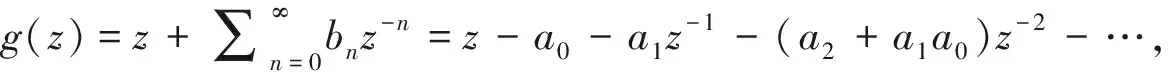
猜你喜欢
上海师范大学学报·自然科学版(2022年3期)2022-07-11
北京航空航天大学学报(2022年5期)2022-06-06
初中生学习指导·提升版(2022年4期)2022-05-11
黑龙江大学自然科学学报(2022年1期)2022-03-29
云南大学学报(自然科学版)(2022年1期)2022-02-21
中学生数理化(高中版.高二数学)(2021年5期)2021-07-21
校园英语·上旬(2020年1期)2020-05-09
商情(2019年9期)2019-04-01
卷宗(2017年16期)2017-08-30
考试周刊(2016年44期)2016-06-21

