具有状态传感器故障的非线性系统容错稳定控制
付启龙, 龚建业, 沈启坤
(扬州大学信息工程学院, 江苏 扬州 225127)
随着现代化工业的发展,企业对生产过程的安全性和生产设备的可靠性要求越来越高,在此条件下,故障容错控制吸引了越来越多的关注.在故障容错控制的研究中,非线性系统的研究占据着十分重要的地位,已取得丰硕的研究成果.Jiang等[1]针对非线性系统时变过程中出现的故障,提出了一种新的估计方法,并设计了容错控制器,通过稳定闭环系统来补偿故障的影响; Efimov等[2]研究了非线性系统未知输入估计和补偿的问题,提出了一种基于高阶滑模差分和离散时间优化技术的方案;Tong等[3]提出了基于后推技术的动态面控制设计方法,用于设计自适应分布跟踪容错控制器.由于神经网络有着强大的学习能力和逼近非线性函数的能力,一些研究人员则采用神经网络来逼近实际系统中的非线性项[4-5].Zuo等[6]提出了存在固定增益控制器的充分条件,保证了闭环系统在所有可能故障下的规律性、无脉冲和稳定性,并提出自适应容错控制器,通过估计故障和在线更新参数矩阵来补偿系统的故障影响; Shen等[7]讨论了具有执行器故障的不确定非线性系统的容错动态面控制问题,采用了一种主动容错控制方案,并运用动态面控制技术,提出了一种新颖的故障诊断算法,消除了具有输出误差且时间导数已知的经典假设; Li等[8]研究了非严格反馈非线性系统的主动容错控制问题;Tong等[9]研究了严格反馈形式的不确定随机非线性系统模糊自适应执行器故障补偿控制;Wang等[10]针对具有建模不确定性和执行器故障的非线性系统,采用滑模控制,利用不同的设计参数分别处理建模不确定性和执行器故障;Chen等[11]研究了数字通信网络中具有未知时变执行器故障的非线性系统鲁棒控制问题. 本文针对一类具有状态传感器故障的非线性系统,考虑了存在外部干扰的情况,拟利用神经网络的逼近能力,提出一种自适应容错稳定控制方案.
1 问题描述与基本假设
考虑非线性系统
(1)
其中系统状态x=[x1…xn]T∈Rn, 系统输入u∈R, 系统输出y∈R,f(x)∈R是未知的光滑函数,有界函数h(t)∈R表示外界未知干扰.设状态传感器故障模型为xf=x+bf, 其中xf=[xf1xfn]T∈Rn, 状态传感器的偏置故障bf=[bf1…bfn]T∈Rn.控制目标: 设计一个自适应控制律u, 使系统渐近稳定, 同时保证闭环系统中所有信号半全局一致终结有界.
假设1存在未知实常数h*>0, 使得|h(t)|≤h*.
假设2对于状态传感器故障模型, 存在一个未知实常数b0>0使得‖bf‖≤b0.
本文利用径向基神经网络逼近未知连续函数f(x).在一个闭集上,神经网络能以任意精确度逼近任意连续函数[12-13], 但状态发生故障时,神经网络的输入就不是真实的状态x而是被故障干扰的状态xf,故本文在利用神经网络逼近系统(1)中未知光滑函数f(x)时,做如下变换:f(x)=W*TS(x)+ε=W*TS(xf)-W*T(S(xf)-S(x))+ε.
假设3存在未知正实常数ε*和wm, 使得|ε(x)|≤ε*, ‖W‖≤wm.
2 结果与讨论
2.1 控制器设计

2.2 稳定性分析
3 仿真结果

图1 x1, x2随时间t的变化轨迹Fig.1 Trajectories of x1 and x2 with time
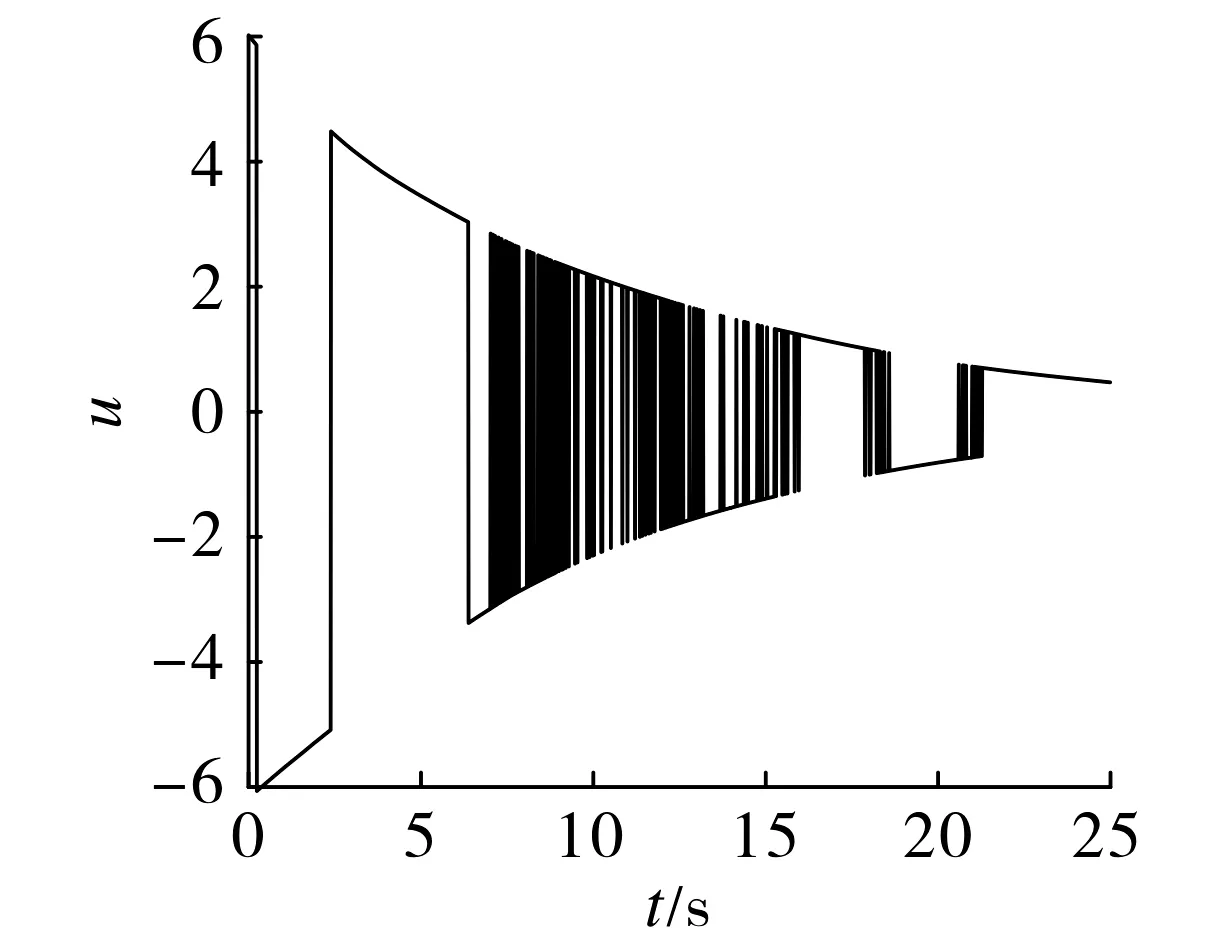
图2 控制信号u随时间t的变化Fig.2 Variation of control signal u with time

图和随时间t的变化Fig.3 Variation of estimated

