基于分支界定法的发电机开停机分配问题的研究
赵海颐,彭泽峰,李丛昀,崔圣
基于分支界定法的发电机开停机分配问题的研究
赵海颐,彭泽峰,李丛昀,崔圣
(三峡大学 电气与新能源学院,湖北 宜昌 443002)
电能,作为最受人类关注的二次能源,有着易转化、好生产等优势,作为人类社会不可或缺的一部分,它扮演着至关重要的角色。以每天各时段用电需求和已有发电机各类数据作为已有条件,进行时间段的划分,将一非线性且非整型问题转化为一线性整型问题,利用分支界定法,建立优化模型,使用Lingo进行求解,研究了发电机如何使用才能既满足用电需求又使成本最低的混合整数规划问题,提高了发电机的使用效率。
发电机;混合整数规划问题;分支界定法;优化模型
1 引言
电能的利用是人类第二次工业革命的标志,它代表了人类社会进入了电气时代。20世纪,人类社会开始出现以电力系统为传输能量中枢的工业社会,对以电磁为基础的信息科学的发展起到巨大的推动作用。在中国,为努力推动社会经济全面发展而抓紧实施电气化建设,电气化建设这个目标似乎并没有终点,目前,还没有人能够预见下一次能源的大转变方向,同时,也很难预测到未来社会电气化的程度[1]。电能,作为一种二次能源,便于从多种途径获得,且易于转化为其他的能源,用以满足生活生产和建设的需要。与其他能源相比,电力的易生产、易传送、易调控的特点使它成为最为理想的二次能源,在人类世界里扮演着重要的角色,因此建设电气化社会是十分有必要的。
本文首先利用已知数据将发电机运行成本划分为三部分,即固定成本、边际成本和启动成本。在此基础上增加约束条件,达到利用分支界定法的程度,做出对时间段的划分,利用Lingo程序求解结果,进而预测一周内的运行成本,以实现最优的发电机分配安排。
2 发电机开停机分配模型的建立与求解
2.1 模型构建
在已有需求的情况下,针对不同配置型号的发电机,将每日用电需求分为七个时间段,在不同时段满足供电需求,并使发电成本最小,这是一个把非线性化成线性、非整型化成整型的动态规划和资源配置问题,即混合整数规划问题。
发电机只要开启,就会有固定成本,所以某天所有发电机的固定成本可用下式表示:

式(1)中:1为某天所有发电机的固定成本;ij为运行时间;Gi为型号为的运行发电机台数;Gi为型号为的发电机的固定成本。
当发电机运行发电功率大于其最小输出功率时,大于最小输出功率这一部分是边际功率,这一部分的发电成本就是边际成本。所以,某天所有发电机运行的边际总成本可用下式表示:

式(2)中:2为某天所有发电机运行的边际总成本;ij为型号为在时间段为的每台发电机的实际输出功率;gi为型号为型号的发电机的最小输出功率;gi为型号为的发电机的每千瓦的边际成本。
当第一天00:00开启发电机时,所有的发电机都有启动成本,启动总成本等于启动发电机总台数与该种发电机启动成本之积,但是从这个时刻之后只有时段始端新开启的发电机才有启动成本。要计算启动总成本就先要了解发电机的变化情况,得到发电机的启动总台数。
使用后一个时间段的型号发电机数量减去前一个时间段的型号发电机数量就可以得到后一时间段的发电机启动台数,因为关闭发电机不需要成本,所以当得到发电机启动台数小于等于0时,都认为启动台数为0台,从而不需要启动成本。时间段型号发电机的启动(变化)台数如下式所示,其中默认0时刻前一时刻所有型号发电机已开启数量为0台:
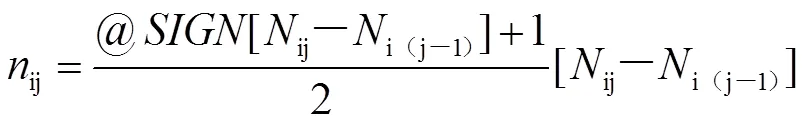
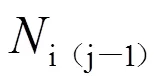
启动成本为:
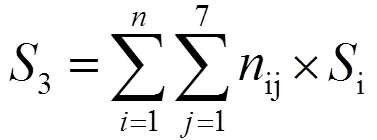
式(4)中:i为型号为的发电机的启动成本。
要使每日总成本和一周总成本最小的模型为:

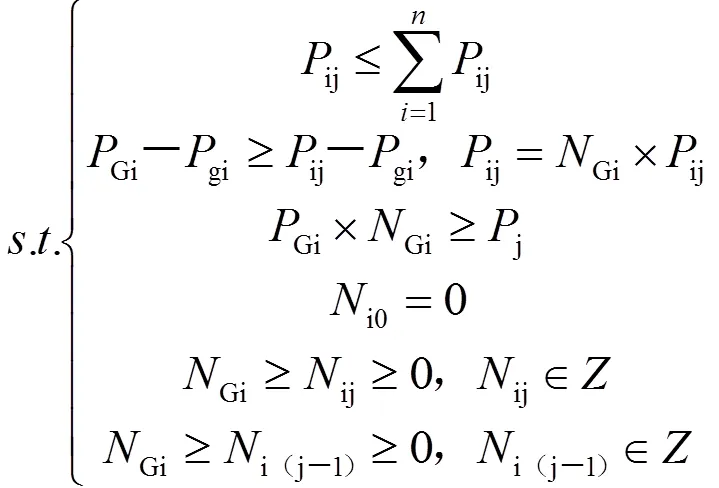
2.2 模型求解
本文采用分支界定法[2],求解此混合整数规划问题。先对其进行整数规划的线性规划求解,如果最优解是整数,则满足该问题的条件,假如最终结果不是一个整数,此时直接向上取整得到的结果在某些时候可能并不是一个最优解。因此求出整数规划的上下界,用增加约束条件的方法,再将该线性规划的区域划分出多个可行的子区域(或称分支),再对这些区域求解线性规划的问题,多次进行后,子区域逐渐缩小,就可得到该问题的最优解。
本题采用Lingo[3]进行编程解答,流程如图1所示。Lingo可用于一些线性或者非线性的方程求解,十分适合求解优化模型。
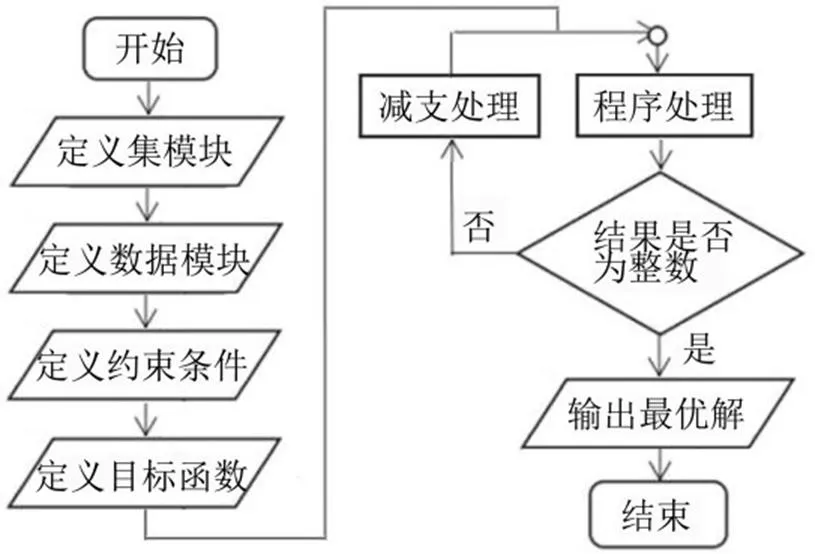
图1 分支界定法程序求解流程图
以四种型号的发电机为例,利用Lingo进行求解,整理所得结果,求解得每天各时段发电机运行台数,如表1所示。
表1 每日各时段发电机运行台数
型号时间 00:00—06:0006:00—09:0009:00—12:0012:00—14:0014:00—18:0018:00—22:0022:00—24:00 型号1发电机3101010101010 型号2发电机4434444 型号3发电机0888882 型号4发电机2333232
运用Lingo求解得出1 d的最小成本mind=230 060元。进而预测出1周的最小成本为min=1 596 680元。
3 结果分析
3.1 对Reduced cost进行分析
“”表示当变量有微小变动时,目标函数的变化率。其中,基变量的值应为0,对于非基变量(,),相应的值表示当某一个变量(,)增加一个单位时目标函数的增加量。例如变量(1,6)对应的值应为-4 480,表示当非基变量(1,1)的值变化时(此时假设其他非基变量保持不变,但为了满足约束条件,基变量显然会发生变化),最后目标函数值=230 060-4 480=225 580元。
3.2 Slack or surplus及Dual price的解释
“”是给出松弛变量或剩余变量的值,两种变量的取值能够表达现行的可行点是在可行域的内部还是其边界,即在取此可行解时,原来的约束条件是否成立;“(对偶价格)”表示当对应约束有微小变动时,目标函数的变化率,即目标函数对约束条件的一阶偏导数,满足条件。
3.3 其他分析
其结果经推理较合理,输出结果中对应的每一个约束有一个对偶价格,如果其数值为,表示对应约束中不等式右边如果增加一个单位,目标函数增加个单位。因此,如果在最优解处取等号(即“紧约束”也成为有效约束或者其作用约束),对偶价格才可能不是0。
因此,按上述方法对发电机开停机进行分配可实现最优分配,能够提高发电机效率并减小成本,具有实际参考价值。
4 结束语
本文探究的是发电机的开停机分配情况与成本问题,属于混合整数规划模型,首先对数据进行分析,进行时间段的划分,并使用分支界定法建立模型,然后利用Lingo进行分析求解,给出最优的发电机使用分配情况方案,提高发电机的使用效率,降低成本。此外,该模型可推广至生产过程中生产资料的生产设备的分配问题,例如运输过程中的运输工具的分配问题,例如货船、货车的分配问题;设备安装的分布问题,例如舞台现场灯光、音响的布置等,对解决最优分配问题具有现实意义。
[1]吴汉荣.电气化在工业领域中的应用与发展研究[J].山东工业技术,2017(3):33.
[2]李博涛,王之琪,王秀彩.分支界定法在特征向量提取中的应用[J].山西电子技术,2011(2):37-38.
[3]熊文涛,肖应雄.LINGO软件在目标规划实验教学中的应用[J].新疆师范大学学报(自然科学版),2019,38(1):65-69.
G434
A
10.15913/j.cnki.kjycx.2019.13.008
2095-6835(2019)13-0019-02
赵海颐(1999—),女,研究方向为电气工程及其自动化。
〔编辑:张思楠〕

