基于贝叶斯网络的某型导弹状态评估

田述栋，刘崇屹，宋代宗

（91049部队，山东青岛266102）

随着科学技术的不断发展，各种高精尖技术广泛应用于某型导弹中，大大提高了导弹的综合性能，这就对导弹的维护保障提出了更高的要求。长期以来，大部分学者将某型导弹故障的预防和检测作为研究重点，一旦发生故障，可以快速准确定位、排除和处理故障。但对导弹当前处于何种状态、何时发生故障却少有研究。因此，迫切需要采取科学高效的手段评估导弹当前的状态，进而开展基于状态的预防性维修工作，提高导弹的战备完好性，夺取战场环境主动权。

20世纪60年代初，美国国防部明确规定“没有评估模型的新武器研制项目不予立项[1]”，这成了武器装备状态评估技术发展的契机，大量评估方法模型应运而生且各有所长。神经网络评估方法[2-3]自适应、泛化、容错能力强，适用于多类别状态的评估，但是全局解释能力差强人意，并且需要大量训练样本，往往难以满足要求；支持向量机[4-5]即使在样本较少的情况下也能得到最优解，但是分类器中核函数的选择缺乏令人信服的统一标准；模糊综合评判法[6-7]对定性定量指标统一表示，能够出色地解决模糊性问题，但是隶属度函数的确定是个难点；灰色评估方法[8-9]擅长处理小样本、贫信息问题，但是容易出现多个灰类交叉以及各个灰类聚类系数相近的无差异性现象。

贝叶斯网络[10-11]因其突出的概率表达能力、不确定问题处理能力和多源信息融合能力在不确定推理领域占据重要地位。将贝叶斯网络应用在导弹状态评估中具有如下优势：图形化概率表达方式符合人类思维模式，便于推理，用“边”描述变量之间的因果关系，用条件概率表达其关系强弱；贝叶斯网络本身就是表达不确定性的模型，与导弹所处状态的不确定性相符；贝叶斯网络能够融合多源信息，尤其是高度冲突的信息，可以同时融合多种状态影响因素建立模型，并且避免出现与事实严重不符的情况；贝叶斯网络拓扑结构灵活，具有全局更新能力，可以推广应用于不同型号导弹状态评估模型的建立[12-13]。

因此，本文在综合考虑某型导弹测试信息和定性信息的基础上，提出了一个基于贝叶斯网络的某型导弹状态评估方法。结合专家打分法，建立了多状态信息融合的贝叶斯网络模型，实现了某型导弹定性和定量状态信息的有机结合。

1 状态等级的重新划分

对某型导弹的状态进行评估前须要确定其状态等级。传统的“是非制”评估方法只是简单地将其划分为“故障”和“正常”2种状态[14-16]：若某型导弹的所有测试参数均在规定的范围内，就认为某型导弹“正常”；否则为“故障”。不仅无法确切地知晓某型导弹的性能退化程度，而且若在制定维修策略时不加以区分，则会导致“无病医治”或者“有病不治”的情况发生。因此，本文结合实际情况将某型导弹的状态进行重新划分，如表1所示。

表1 某型导弹状态划分Tab.1 Quality state level division of a certain type of missile

2 状态信息的评估

2.1 定量状态信息的评估

现有某型导弹的状态评估方法通常以测试信息作为定量状态信息。导弹的性能测试参数种类多样，各个测试参数的量纲和阈值往往不同。因此，为了方便下一步网络推理，在确定其状态之前需要对各个测试参数进行归一化处理，利用归一化值表征相应测试参数的状态。归一化函数为：

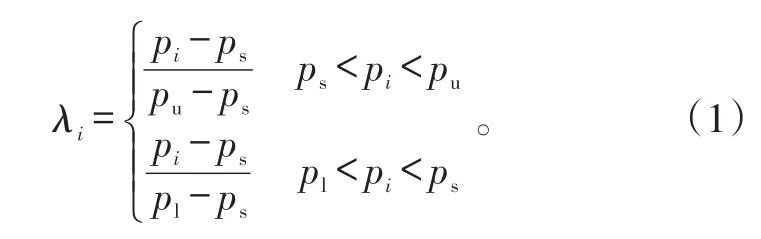
式（1）中：pi为第i个测试参数的实测值；ps为标准值；pu为上阈值；pl为下阈值。

不难看出，当λi趋近于0时，实测值趋于标准值，测试参数处于最佳状态；当λi趋近于1时，实测值趋于上阈值或者下阈值，测试参数处于最差状态。

划分的“优”、“良”、“中”、“差”4个状态等级之间不存在明确的界线划分，只存在模糊的过渡区域，因而借鉴模糊集合理论提出一种改进的隶属度函数，表征测试参数与4个状态之间的隶属关系，如图1所示。

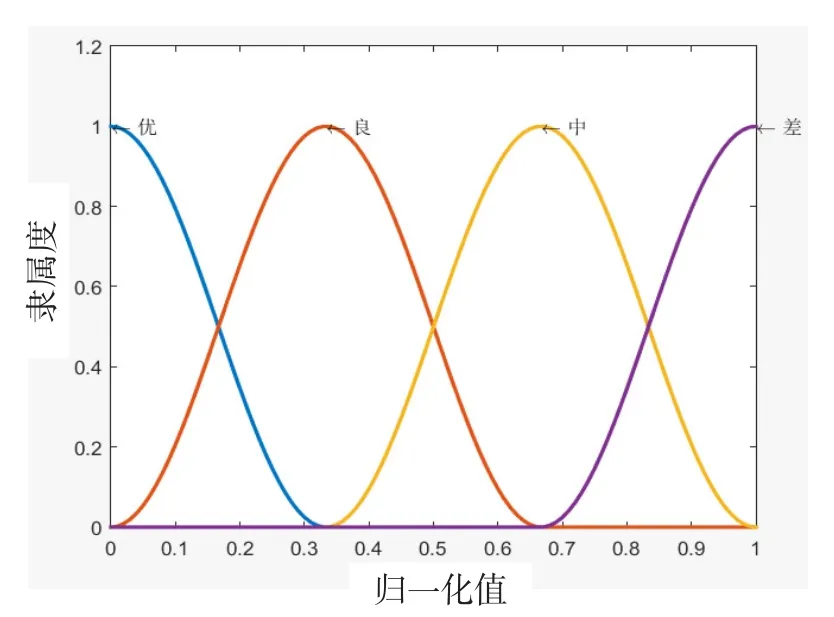
图1 改进隶属度函数Fig.1 Improved distribution affiliation function

从图1中可以看出，改进的隶属度函数可以量化表示相邻状态等级之间的不确定性。也就是说，每个测试参数均以不同的隶属度分别属于2个状态等级，且隶属度之和等于1。

各个性能测试参数的归一化值对应的隶属度函数分别为：

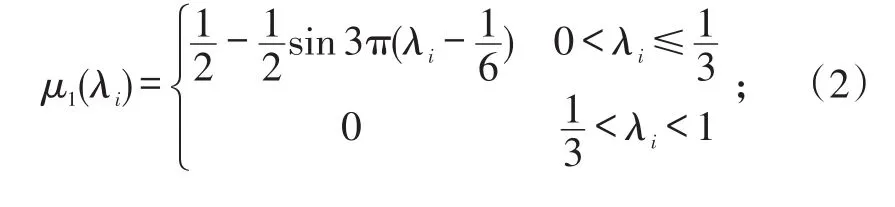
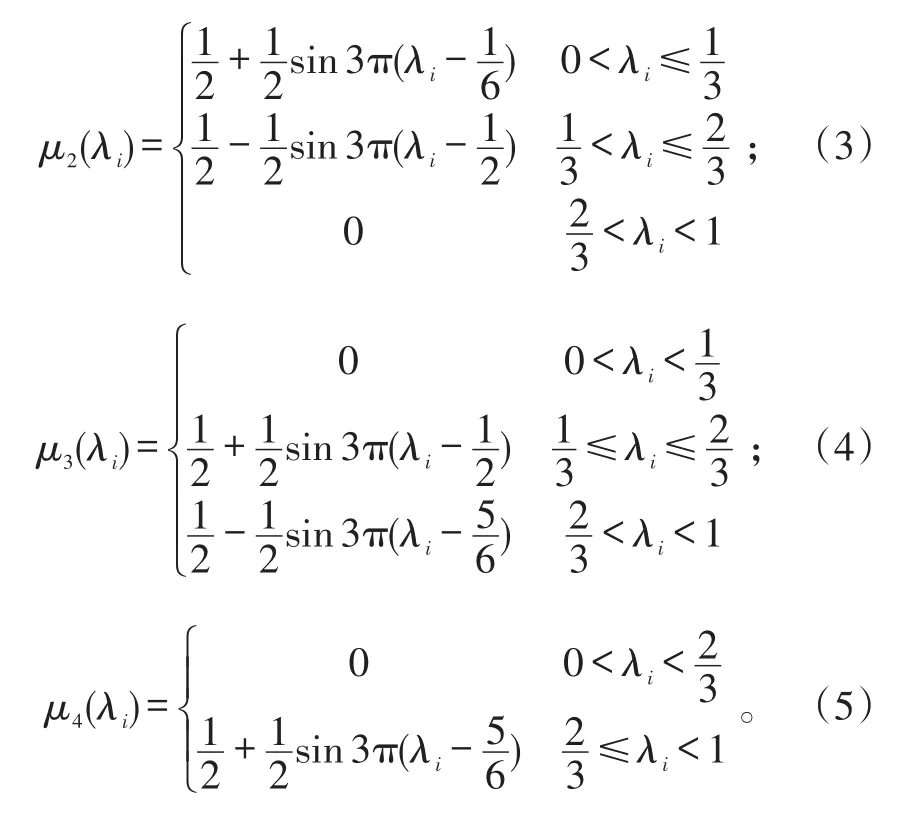
μ1(λi)、μ2(λi)、μ3(λi)、μ4(λi)分别为第i个测试参数的归一化值λi隶属于“优”、“良”、“中”、“差”4个状态等级的隶属度函数。

2.2 定性状态信息的评估

某型导弹的状态是包含测试信息在内的多种类型影响因素共同作用的结果。仅仅依据测试信息得到的状态评估结果的可信度不高，因而考虑结合定性状态信息进行评估。定性状态信息主要指对导弹定性要求满足程度的描述。

对某型导弹定性信息的状态进行评估时，只要某定性指标不满足规定要求，则认为该定性指标是故障的，直接判定导弹为“故障”状态。若某定性指标满足规定要求，则该定性指标是正常的，即处于“优”、“良”、“中”和“差”中的某一个具体状态。考虑到定性指标的描述和评估往往具有一定的模糊性和随机性，本文采用云模型[17]处理这种不确定性。

假设某型导弹有N个指标s1,s2,…,sN，邀请k位专家e1,e2,…,ek沟通协调后，分别给出各个指标的总评分范围[di,ui]（0≤di＜ui≤1;i=1,2,…,N）。

采用指标近似法对评分范围区间进行云化得到云模型Ci=((Ex)i,(En)i,(He)i)（i=1,2,…,N）。

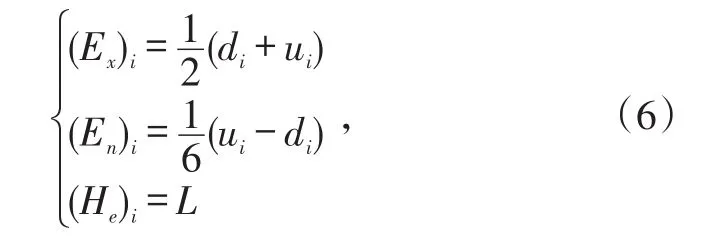
式中，L为常数，通常由人为指定。

专家给出的“优”、“良”、“中”和“差”4个状态等级的评分范围为[ay,by]（0≤ay＜by≤1;y=1,2,3,4），同样得到相应的云模型Ty=((Ex)y,(En)y,(He)y)。

计算N个指标隶属于4个状态等级的隶属度，具体算法如下。

输入：云模型Ci=((Ex)i,(En)i,(He)i)和Ty=((Ex)y,(En)y,(He)y)，云滴数Nc。

输出：云模型Ci=((Ex)i,(En)i,(He)i)和Ty=((Ex)y,(En)y,(He)y)的隶属度γ(Ci,Ty)。

Step1：生成一个以(En)i为期望、(He)i为标准差的正态随机数 (E′n)i。再以 (Ex)i为期望、(E′n)i为标准差生成正态随机数xi，作为云模型Ci=((Ex)i,(En)i,(He)i)的一个云滴。

Step2：以(En)y为期望、(He)y为标准差生成正态随机数 (E′n)y。

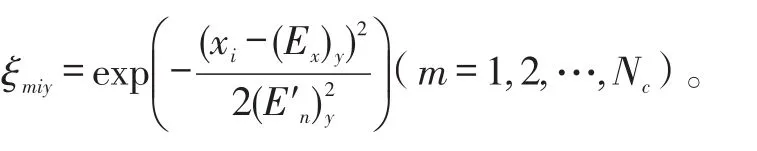
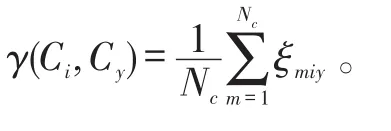
3 基于贝叶斯网络的多状态信息融合评估模型

确定了某型导弹各个状态信息的状态等级之后，难点就在于融合各个信息的状态以确定整个导弹的状态等级[18]。因此，选用多源信息融合能力较为出色的贝叶斯网络建立多状态信息融合的评估模型。

3.1 评估模型的构造

依据某型导弹的状态信息（包括定性和定量状态信息），只要存在状态信息不满足规定要求，例如某型导弹的单个或者多个测试参数超出规定的阈值范围或者某定性指标不满足规定的要求，则直接判定导弹是“故障”的；若导弹全部的状态信息均满足规定要求，则导弹处于“优”、“良”、“中”和“差”中的某一个具体状态。此时，某型导弹的定量状态信息和定性信息均能够反映该导弹的状态，对导弹状态的评估问题则可以视为多状态信息的融合问题，即可以在评估定量状态信息和定性信息状态评估结果的基础上，通过贝叶斯网络融合全部状态信息确定导弹的最终状态等级。最终设计出的评估模型如图2所示。

3.2 评估流程的规划

首先，评估状态信息。判断某型导弹的全部状态信息中是否存在不满足要求的情况。若存在，则直接给出该导弹的状态等级为“故障”；否则，分别对导弹的测试参数和定性信息进行评估，确定各个状态信息对应于“优”、“良”、“中”和“差”4个状态等级的状态隶属度。

其次，建立贝叶斯网络。构造贝叶斯网络拓扑结构，将各状态信息对应于“优”、“良”、“中”和“差”4个状态等级的状态隶属度作为贝叶斯网络的根节点状态，构建条件概率分布表，进而建立贝叶斯网络。

最后，融合多状态信息。根据建立的贝叶斯将各个状态信息进行融合，最终得到整个导弹处于“优”、“良”、“中”和“差”状态等级的概率。评估流程如图3所示。

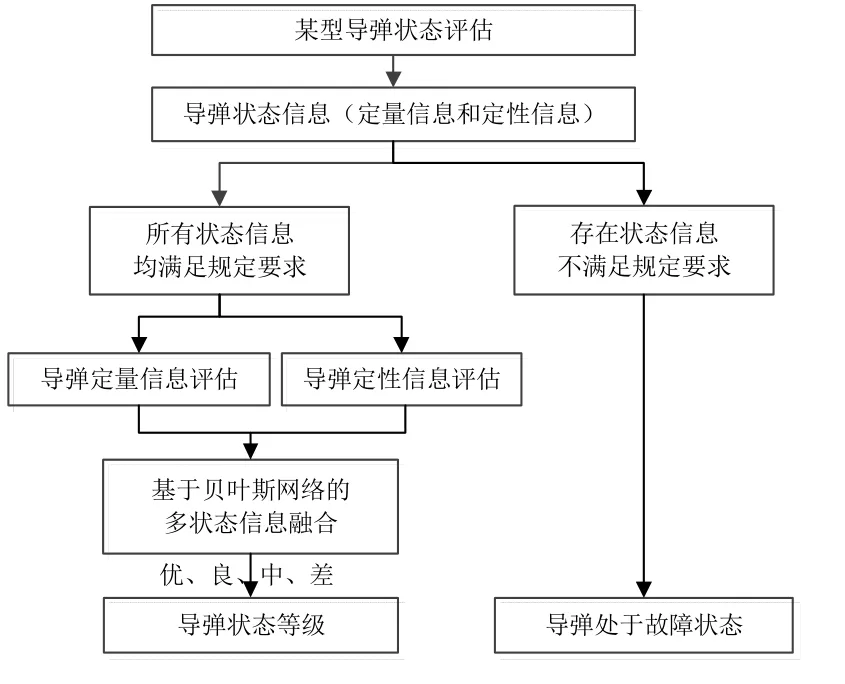
图2 状态评估模型Fig.2 State evaluation model

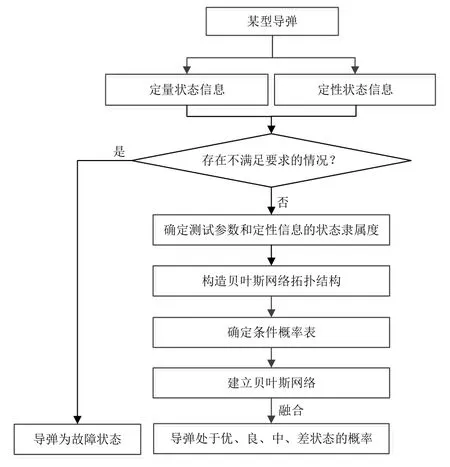
图3 状态评估流程图Fig.3 Flow chart of state evaluation

3.3 贝叶斯网络的建立

1）贝叶斯网络拓扑结构的构造。贝叶斯网络的拓扑结构是贝叶斯网络的重要组成部分。目前，常用的构造方法分为参考专家经验的手动构造法和通过智能算法进行数据学习的自动构造法。考虑到某型导弹的评估知识比较完善，因而邀请领域内专家确定的某型导弹状态评估贝叶斯网络拓扑结构见图4。

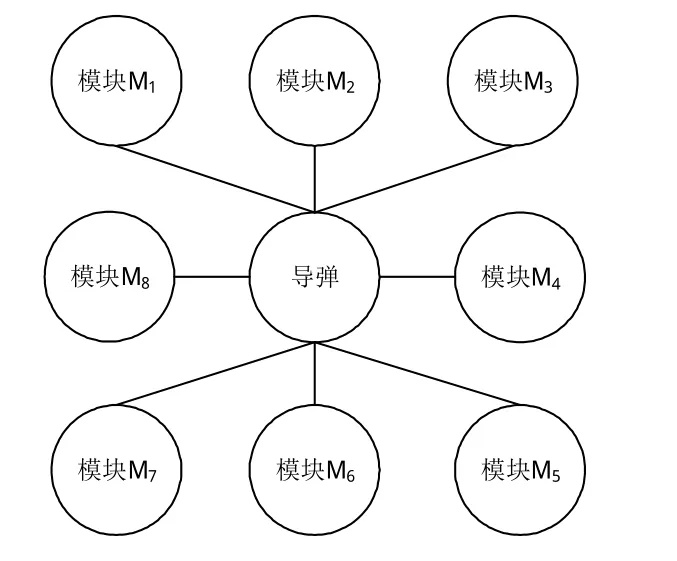
图4 导弹拓扑结构图Fig.4 Topology chart of missile

其中，根据专家意见将某型导弹共划分为8个模块，并且这8个模块均包含多个子单元，因而它们都是中间节点，可以继续建立中间节点的下一层拓扑结构，以模块M1为例构建的拓扑结构如图5所示。

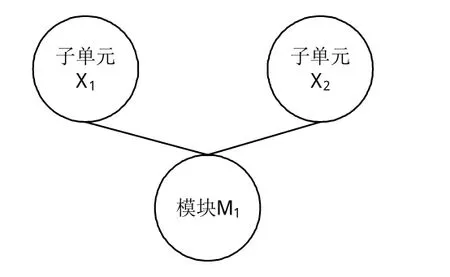
图5 模块M1拓扑结构图Fig.5 Topology chart of moduleM1

2）条件概率表的构建。确定了贝叶斯网络各个根节点状态和拓扑结构，难点就落在了贝叶斯网络条件概率表的创建上。目前，主要有参数学习和专家咨询2种方法。考虑到某型导弹组成部件众多、各个元器件之间关系密切，导致其贝叶斯网络结构复杂，节点之间大多为非逻辑关系，参数学习过程比较繁琐，因而往往采用咨询专家的方法，即通过专家之间相互沟通给出最终的条件概率表。

4 举例分析

以贮存状态下的某导弹为研究对象，考虑到状态信息众多，这里以其某子单元X1为例，其余子单元和模块可以按照相同的方法完成评估。

4.1 状态信息的评估

以测试参数V1和V2的假设值为例，利用式（1）进行归一化处理，分别代入式（2）～（5）中，计算出隶属于“优”、“良”、“中”、“差”4 个状态等级的隶属度，如表 2所示。

以子单元X1的接口因素V3为例，10位专家给出的评分范围为[0.999 7，0.645 1]，代入式（6）计算得相应的云模型为C(0.822 4,0.059 1,0.005 2)。同理得到“优”、“良”、“中”、“差”4 个评价等级云分别为T1(0.948,0.017 3,0.005 2)、T2(0.850,0.015 3,0.004 6)、T3(0.686,0.039 3,0.009 1)、T4(0.284,0.094 7,0.013 9)。进而计算得出接口因素V3隶属于4个状态等级的隶属度分别为55.62%、37.88%、6.29%和0.21%。

表2 定量状态信息评估Tab.2 Evaluation of quantitative state information

4.2 多状态信息的融合

构造子单元X1的贝叶斯网络拓扑结构如图6所示，邀请10名专家给出相应的条件概率表，经过推理即得到整个子单元X1处于“优”、“良”、“中”、“差”4个状态等级的可能性依次为0.401 7、0.348 0、0.170 4和0.079 9，即处于“优”状态并且正向“良”状态过渡。

构建整个导弹的贝叶斯网络拓扑模型，输入所有状态信息的假设值，最终确定其处于“优”、“良”、“中”、“差”4个状态等级的可能性分别为0.124 6、0.396 9、0.381 8和0.096 7。

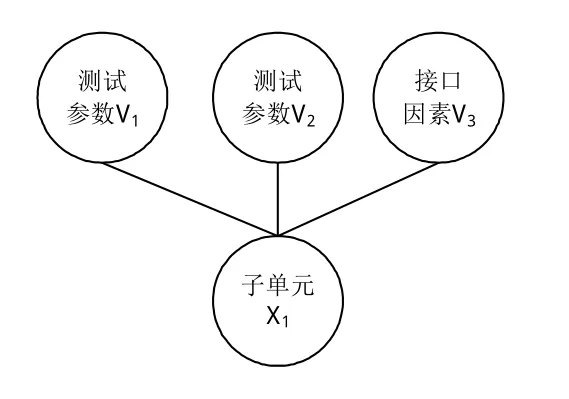
图6 子单元X1拓扑结构图Fig.6 Topology chart of sub element

5 结束语

针对传统“是非制”导弹状态评估方法的不足，本文对某型导弹的状态等级进行了重新划分，并且兼顾了其测试定量信息和定性信息，提出了一个基于贝叶斯网络的导弹状态评估方法，给出了某型导弹的最终状态等级，实现了定性状态信息和定量状态信息的有效融合。通过某型导弹状态评估的举例分析验证了所提方法的可行性和合理性，主要结论如下：

1）给出了一种改进的隶属度函数表征测试参数与状态等级的隶属度，克服了状态等级之间界线划分不明确的问题；

2）采用云模型表征导弹定性信息的状态隶属度，不仅能够处理定性信息的随机性和模糊性，而且避免了仅仅依据导弹测试信息评估导弹状态导致的评估结果可信度不高的问题。