基于模糊动态逆的飞机直接升力控制

梁洪瑜，张 勇，徐 鸣

（1.海军航空大学，山东 烟台264001；2.海军装备部，北京100071）

直接升力控制方法诞生于20世纪60年代，其发展大致可分为3个阶段[1-3]。第一阶段，主要从理论的角度分析直接升力控制的机理和用途；第二阶段，直接升力控制方法被运用到一些验证机上，实现了从理论研究到工程应用的转化；第三阶段，结合现代控制理论进行直接升力控制律的设计。与传统飞行控制方法相比，直接升力控制能够解除飞行轨迹同飞机姿态的耦合，能够实现对飞行轨迹的直接控制，从而使得飞行轨迹的响应比传统飞机更快。直接升力控制方法的这些特性对于飞机的机动飞行和舰载机的着舰“保角”飞行都有十分显著的意义。

直接升力控制的实质即为解耦控制。目前，能够实现解耦控制的方法有很多，包括特征结构配置法[1]、逆奈奎斯特阵列法[2]、LQG/LTR方法[4]以及高增益串联渐进解耦控制方法[5]等。为了增强控制系统的鲁棒性，杨向忠等人[6]设计过一种带优化修正函数的模糊控制系统，之后张筱磊[7]、马小娟[8]、杜金刚[9]等人在进行鲁棒直接升力控制的研究中基本上沿用了这一方法。李林侃等人[10]在设计直接升力控制系统时，将H-∞理论同动态逆理论结合，设计了一种鲁棒动态逆控制器，使系统的动态性能和鲁棒性能均有所改善。鲁可、袁锁中等人[11]将定量反馈理论融入动态逆控制系统中，同样在实现解耦的基础上达到了良好的系统动态性能和鲁棒性。此外，μ综合方法[12]、线性二次型高斯方法[13]也被用以增强直接升力控制系统的鲁棒性。

本文在设计控制系统过程中，用模糊控制器分别控制已用动态逆控制器完成解耦的迎角和俯仰角通路，并在优化目标函数中引入对超调量的约束，对模糊控制器参数进行优化后，设计出以实现飞机直接升力控制为目的的一种模糊动态逆控制器。数值仿真结果表明，本文设计的模糊动态逆控制器能够实现直接升力控制，并且具有一定的鲁棒性，在动态响应上也优于单纯的动态逆控制器。

1 飞行动力学建模

本文以AFTI/F-16飞机为研究对象，其纵向上的受力分析及相关角度如图1所示。

图1 飞机纵向受力及相关角度示意图Fig.1 Longitudinal force and attitude angle of the aircraft

直观来看直接升力控制是对飞机飞行轨迹的直接控制，而实质上是对飞机迎角和俯仰角的解耦控制。由图1可以看出，飞机的迎角、俯仰角、航迹角具有关系α=θ-γ。直接升力的3种模态中，单纯直接升力模态是保持迎角α不变的控制，机身俯仰指向模态是保持航迹角γ不变的控制，垂直平移模态是保持俯仰角θ不变的控制。因此，仅研究直接升力控制时，只需考虑与飞机姿态有关的动力学方程即可。

飞机纵向上角度的控制方程如式（1）所示。假定飞机安装有保持速度恒定的动力补偿系统，基本能够保持飞机速度不变。同时，考虑到飞机速度的响应相对于角度的响应慢得多，因此能够将速度引起的力和力矩的变化略去[14]。根据以上假设，在气流坐标系下将式（1）在基准状态进行小扰动线性化后，得到飞机α、q、θ变化的状态空间方程如式（2）所示。

AFTI/F-16飞机的主要参数如表1所示[15]。

表1 AFTI/F-16飞机主要参数Tab.1 Main parameters ofAFTI/F-16 aircraft

参考文献[15]，将AFTI/F-16飞机的气动数据代入式（2），即可得到飞机姿态变化的状态空间方程：

式（3）中：状态变量x=[ΔαΔqΔθ]T；控制变量u=[ΔδeΔδf]T；状 态 矩 阵 和 控 制 矩 阵 分 别 为

2 控制器设计

2.1 动态逆控制器的设计

假设MIMO系统的状态空间方程为：

式（4）中：状态向量为x(t)∈ℝn；输入 向 量 为u(t)∈ℝm；输出向量为y(t)∈ℝp；A为n×n矩阵；B为n×m矩阵；C为p×m矩阵。

假设系统为正方系统，满足m=p，且输入信号用r(t)表示，则系统输出跟踪输入信号的误差为：

对系统的输出方程求导，直至其表达式中出现输入向量u(t)，即：

若矩阵CB可逆，则定义一个辅助输入：

然后，可得输入向量表达式为：

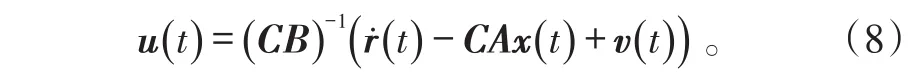
取v(t)=Ke(t)代入式（7），得系统误差动态方程：

只需选取合适的矩阵K，即可使系统稳定并且实现控制解耦[16]。

依据上述步骤设计的动态逆控制器为：

对于矩阵C为单位阵，且矩阵B中存在全零行的情况，则可将式（4）整理成如下形式：

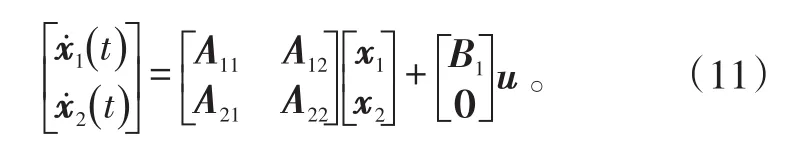
此时状态向量x1(t)的形式满足常规动态逆控制器设计的条件，令

式中，e1=r1-x1。从而能够设计出满足解耦要求的动态逆控制器。

单独采用动态逆方法时，设计的飞行控制系统Simulink仿真图如图2所示。

图2 基于动态逆方法的直接升力控制系统Fig.2 Direct lift control system based on dynamic inverse method

2.2 模糊控制器的设计

动态逆方法要求建立准确的飞机飞行动力学模型。而实际上，这一条件基本不可能满足。当飞机动力学模型不准确或者由于扰动、环境变换导致飞机实际动力学方程内部参数发生微小变化时，单纯使用动态逆方法将无法保证飞行控制的实际效果。为此，本文将模糊控制理论同动态逆控制器相结合，实现直接升力控制的同时，从而保证控制系统的鲁棒性。

模糊控制起源于20世纪60年代，由美国的L.A.Zadeh[17-18]首次提出。它是一种依赖专家经验、以模糊集理论和模糊逻辑推理为基础的智能控制方法，一般主要由模糊化接口、推理机和解模糊接口组成。本文设计的是一种两输入单输出的模糊控制器，通过将这一控制器同动态逆控制器结合使用，最终设计出具备一定鲁棒性的解耦控制系统。

模糊控制器的设计步骤如下：

1）确定模糊控制器结构为两输入单输出的二维模糊控制器。其中，输入变量为误差e及其导数，输出变量为U0。

2）定义输入及输出变量模糊集。令E=ke⋅e，EC=kec⋅。将E、EC、U0分别划分7个模糊集，分别为NB（负大）、NM（负中）、NS（负小）、Z（零）、PS（正小）、PM（正中）、PB（正大）。其中，E、EC的论域均为[-6,6]，U0的论域为[- 3,3]。

3）定义隶属度函数。经过仿真试验，本文采用图3所示的隶属度函数。

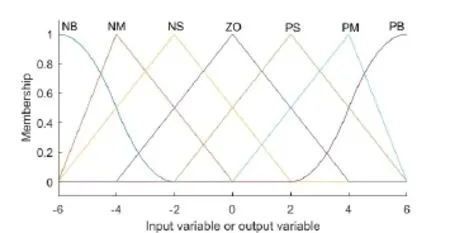
图3 隶属度函数图Fig.3 Membership function plots

其中，输入变量e、的隶属度函数均采用图3所示隶属度函数，横坐标单位分别为rad、rad/s；输出变量为无量纲量，其隶属度函数采用与输入变量相同类型的隶属度函数。其中，论域设置为[- 3,3]。

4）建立模糊控制规则表。根据经验和程序调试，建立模糊控制规则表如表2所示。

表2 模糊控制规则表Tab.2 Fuzzy control rule table

5）反模糊化。为了保证模糊控制器的输出更加平滑，本文采用面积重心法作为反模糊化的方法。面积重心法采用隶属度函数同坐标横轴围成的图形的重心横坐标作为控制输出。

反模糊化方法的数学表达式为：

式（13）中：μ(x)为隶属度函数；x为隶属度函数的横坐标；xo为模糊控制器的最终输出。

将动态逆控制器中的矩阵用模糊控制器代替，即可得到基于模糊动态逆方法的飞机直接升力控制系统，最终系统的Simulink仿真图如图4所示。

图4 基于模糊动态逆方法的直接升力控制系统Fig.4 Direct lift control system based on fuzzy dynamic inverse method

3 仿真分析

3.1 参数优化

图4所示的模糊动态逆控制系统中，存在8个待定参数，即ke1、kec1、ku1、ki1、ke2、kec2、ku2、ki2。

为了使控制系统能够达到理想的响应特性，需要对这些待定参数进行寻优计算。控制系统常用的寻优计算的准则有ITAE准则、ITSE准则、ISTAE准则、ISTSE准则等[19]，这些准则能够使系统参数向着特定的目标进行优化。其中，ITAE准则能够保证系统响应的快速性。

本文考虑到直接升力控制的目的在于对飞行轨迹的直接控制，超调量的存在将使得直接升力控制的效用大大降低。因此，在ITAE准则的基础上，加入正值误差函数的积分项，以约束系统响应的超调量。

本文参数优化时单条通路的目标函数为：

由于误差函数是二维向量，整个控制系统存在耦合，采用分别优化2条通路的方式难以保证最终优化的效果。因此，本文采用同时优化2条通路的方式，并将最终的优化目标确定为：

本文采用序列二次规划（Sequential Quadratic Programming，SQP）算法[20]对控制系统的参数进行优化。

SQP算法是求解非线性最优化问题的一种非常有效的方法，该方法的基本思想是将原问题转化为求解一系列二次规划（Quadratic Programming，QP）问题，经过一步步迭代从而求得最优解。

SQP算法的迭代公式可以用xk+1=xk+αkdk表示，其中，dk是由通过求解QP问题得到的迭代方向，αk是通过修正计算得到的迭代步长。当迭代满足终止条件时，算法结束。

采用SQP算法对图4中控制系统的参数进行优化，其结果见表3。

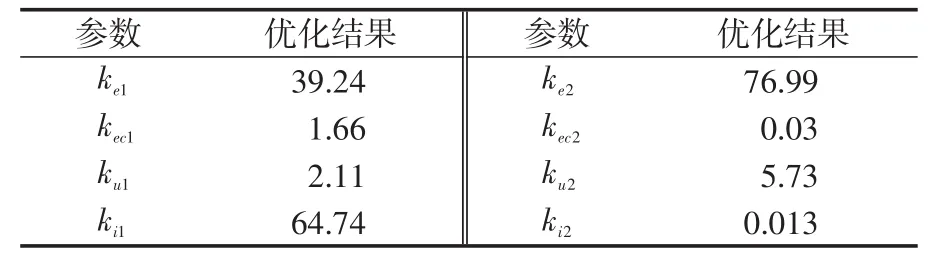
表3 参数优化结果Tab.3 Parameter optimization results

3.2 仿真实验

对本文设计的直接升力控制系统进行仿真。设初始时刻AFTI/F-16飞机在20 000ft的高空以Ma=0.9的速度定直平飞，配平迎角和俯仰角均为1.86°，全动式平尾和襟翼的最大偏转角为±25°，仿真步长为0.001s。

仿真实验1：单纯直接升力控制模态。

在t=0 s时，输入Δα=0，Δq=1(°)/s；在t=1s时，输入Δα=0，Δq=0(°)/s 。这相当于系统输入为Δα=0，Δθ=1，动态逆控制器和模糊动态逆控制器下的仿真结果如图5、6所示。

图5 2种控制器下的迎角和俯仰角响应曲线Fig.5 Angle of attack and pitch angle response curves under two controllers

图6 2种控制器下的舵面偏角响应曲线Fig.6 Control surface deflection response curves under two controllers

仿真实验2：垂直平移控制模态。

在t=0 s时，输入Δα=0，Δq=0(°)/s；在t=1s时，输入Δα=1，Δq=0(°)/s。动态逆控制器和模糊动态逆控制器下的仿真结果如图7、8所示。

图7 2种控制器下的迎角和俯仰角响应曲线Fig.7 Angle of attack and pitch angle response curves under two controllers

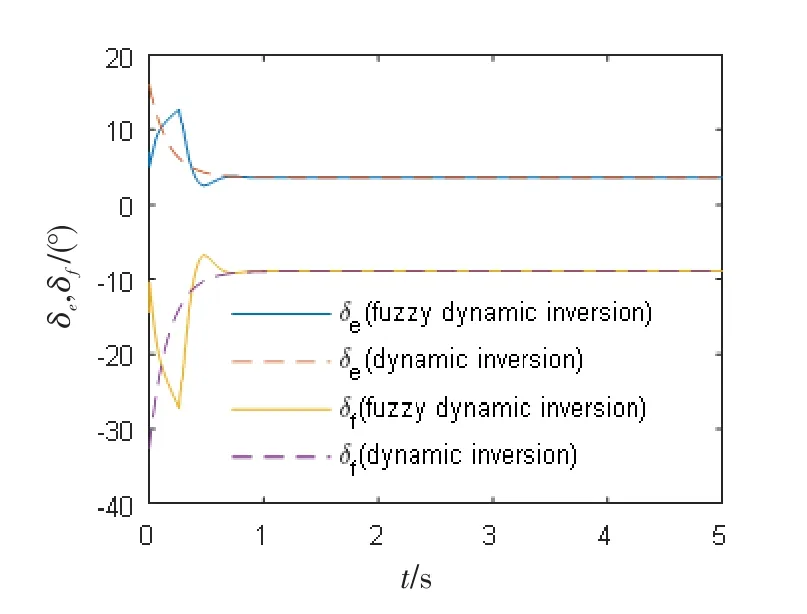
图8 2种控制器下的舵面偏角响应曲线Fig.8 Control surface deflection response curves under two controllers

仿真实验3：鲁棒性验证。

为了验证控制系统的鲁棒性，现假设飞机舵面气动数据发生改变，导致状态空间方程中的输入矩阵产生了-10%的变化，飞机在单纯直接升力控制模态和垂直平移控制模态下的迎角和俯仰角响应如图9、10所示。

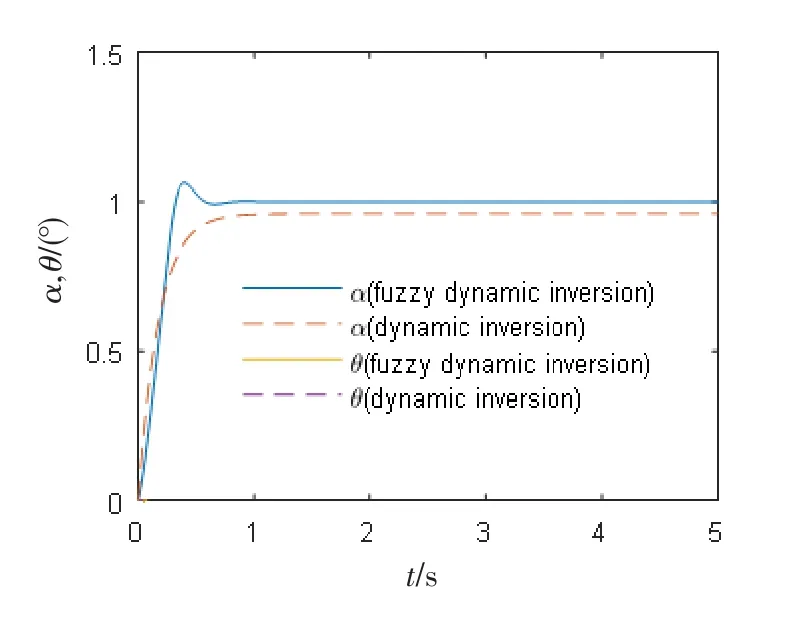
图9 单纯直接升力控制模态下的迎角和俯仰角响应Fig.9 Angle of attack and pitch angle response under simple direct lift control mode

图10 垂直平移控制模态下的迎角和俯仰角响应Fig.10 Angle of attack and pitch angle response in vertical translation control mode

3.3 仿真结果分析

以上3个仿真实验的结果表明：

1）模糊动态逆控制器和动态逆控制器都能够实现直接升力的单纯直接升力模态和垂直平移模态，并且能够直观看出模糊动态逆控制的系统调节时间更短，响应速度优于动态逆控制。仿真实验1不是严格意义上的单位阶跃响应，无法定量分析其调节时间。仿真实验2中，模糊动态逆控制下迎角的系统调节时间为0.435 s，动态逆控制下迎角的调节时间为0.500 s，模糊动态逆控制响应速度更快。

2）仿真实验1中，2种控制器的舵面偏角幅值相同，并且模糊动态逆控制的舵面偏转响应更快，这也是模糊动态逆控制下飞机姿态响应更快的原因。仿真实验2中，模糊动态逆控制的舵面偏转角幅值比动态逆控制更小，因而从这一方面来讲，动态逆控制更优。

3）从仿真实验3可以看出，飞机参数发生微小变化的情况下，2种控制方法仍能实现单纯直接升力控制模态和垂直平移控制模态，但是动态逆控制下飞机迎角和俯仰角响应会存在约5%的稳态误差，这将对实际的飞行控制产生不利影响。

4 结束语

本文提出一种将模糊控制器同动态逆控制器相结合的策略，利用动态逆控制器实现飞机的直接升力控制，利用模糊控制器增强飞机控制系统的鲁棒性。在参数优化过程中，对ITAE性能指标进行改进，引入正向误差积分项从而增加了对系统稳态误差的约束。仿真结果表明，本文所设计的模糊动态逆控制系统优于单纯采用动态逆方法设计的控制系统。本文模糊动态逆控制系统具有良好的指令跟踪性能和解耦性能，能够在实现直接升力控制的基础上快速准确地跟踪系统输入信号；在飞机自身参数发生变化引起状态空间方程参数小幅变化时，本文设计的模糊动态逆控制系统仍然能够准确实现控制目标，证明本文设计的直接升力控制系统具有良好的鲁棒性。