基于改进线性回归模型的民航货物周转量预测

王 琪 李继唐

(1.东北林业大学交通学院,黑龙江 哈尔滨 150040； 2.东北林业大学林学院，黑龙江 哈尔滨 150040)

1 概述

伴随着我国社会主义市场经济的快速发展，作为生产和消费中间环节的交通运输业在发展中的重要作用日益突出。为保证市场的长久向上向好发展，加强交通运输业的管理运行水平势在必行。民用航空运输作为现代化快速运输方式，是其重要组成部分。随着消费水平、生活水平的提高，民航货运需求大幅度上升。中国的航空运输系统在改革开放后得到了快速发展，但总体上仍处于规模小、发展不平衡的成长期。通过合理的预测民航货物周转量，将有利于制定合理的基础设施建设规划，完善其管理运行方法，使其良好适应增长的航空货运需求，有效促进民航货运的快速发展。同时，这将促进交通运输业的多元化系统建设，满足未来货运发展需要[1-3]。

为了保证预测的准确性，选择合适的模型尤为重要。曾广东等人在GM(1,1)对数据进行预测的基础上,采用一种信度马尔科夫链对结果进行修正,新方法引入了Dempster-Shafer(DS)证据理论来描述相对误差所处状态分类的不确定性，建立基本概率指派函数,然后对灰色马氏链的转移概率矩阵进行重新构造,最后根据近期相对误差所处的状态得到将来的状态,进而修正预测结果提高了对货物周转量预测的精确度[4]。李之红等人采用数理统计的方法,得出了三大产业生产总值和5种运输方式所承担货物周转量的相关关系函数,并以此确定了综合货运网络各种运输方式的里程规模。结合当前常规数据结构,建立不同运输方式所承担货物周转量合理比例的多目标货物周转量比例计算模型(CCTV Model),并基于运输效率、运输效益、对经济增长的贡献分别确定了合理货物周转量构成比例[5]。

但是，线性回归模型在某些情况下预测的准确率难以保证。李祚泳等人针对高维、非线性环境系统的传统预测模型存在结构复杂、收敛速度慢、求解精度低的局限,提出对环境系统预测量及其影响因子进行幂函数与对数函数相结合的规范变换，规范变换与误差修正的一元线性回归预测模型简单、预测精度高、稳定性好,不存在“维数灾难”,因而可广泛用于任意系统的预测建模[6]。本文将采用遗传算法对线性回归模型进行优化，以提高线性规划模型在铁路客运量预测中的准确率。

2 预测模型

2.1 研究数据

本文研究数据为1990年—2017年全国民航货物周转量(数据源于《中国统计年鉴2018》)，数据集如表1所示(货物周转量单位：亿吨公里)。

表1 1990年—2017年民航货物周转量

民航货物周转量数据是随年份变化的时间序列，因此年份序列为输入量x，周转量为输出量y。为了使数据分析简单化，需要对输入量进行标准化[8]，标准化过程如下：

(1)

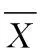
预处理后的数据呈比较明显线性递增趋势，因此本文采用一元线性回归模型对民航货物周转量数据进行预测。取1990年—2014年的数据为训练集，2015年—2017年的数据为测试集。

2.2 线性回归模型

一元线性回归模型根据输入量和输出量的定量关系得出近似直线的函数，民航货物周转量数据在散点图上表现为曲线式增长，因此本文采用多项式拟合来构建预测模型。建模过程如下：

f=p0xn+p1xn-1+…+pn-1x+pn

(2)

(3)

其中，f为预测模型；pn为多项式f的各项系数；n为多项式的次数；L为向量的二范数，即该模型的损失函数[9]。为了确定多项式的次数，本文在python3.6环境下编程(下同)，训练后输出函数图像如图2所示(为了使函数更加直观，输出函数的多项式次数取1,3,5)。

输出各预测模型多项式系数pn和损失值如表2所示。

表2 输出值

所得函数损失值随次数增加而减少，损失值越小说明拟合效果越好，但根据输出函数图像，在多项式次数大于5以后呈现出明显的过拟合现象[10]，因此本文不考虑多项式次数大于5的情况。

为了选出最佳预测模型，本文应用所得5个预测模型对民航货物周转量数据进行预测，所得结果如表3，图3所示。

表3 预测结果

经过对比发现，当多项式次数为2时，预测准确率为0.83，平均误差为37.81，预测效果最好，因此选取最佳预测模型为：

f=16.09x2+56.92x+60.08

(4)

2.3 遗传算法优化模型

本文采用遗传算法优化选取模型的多项式系数求解过程，整体优化过程如图4所示。

遗传算法执行时，应用程序随机生成50个个体，为使运算提高效率和精确度，种群范围设置为：

(5)

向量的二范数越小则适应度越高。因此，式(3)为适应度的目标函数。整体进行交叉操作的概率pm=0.85，每个位进行交换的概率pe=0.5，即个位交叉随机。变异概率pm=0.1，最大迭代次数为100，步长设置为0.6。运行后得到优化模型为：

f=19.97x2+67.84x+60.08

(6)

将其应用到民航货物周转量预测，得到的结果如表4所示。

表4 优化模型预测结果

年份201520162017预测值197.15212.89229.25准确率0.94平均误差11.58

3 结语

本文采用线性回归模型对民航货物周转量进行预测，然后利用遗传算法优化该模型参数计算过程，并将优化后的模型应用进行测试，得到结论如下：利用遗传算法改进线性回归模型可以提高民航货物周转量的精度。优化后的模型，准确率相对提高了0.11，平均误差减少了26.23，预测结果较为准确。