桥墩高度对群桩-承台系统动刚度的影响分析
刘建磊,贺相林,张 勇,马 蒙,王 凯
(1.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081;2.朔黄铁路发展有限责任公司,河北 肃宁 062350)
桥墩基础静刚度反映了在外荷载作用下其抵抗变形的能力。当桥墩基础承载力受沉降变形控制时,竖向静刚度即反映了桥墩基础与变形相关的承载能力。测试桥墩基础的竖向静刚度有2种方法,其一是直接通过静载试验从荷载-沉降曲线的初始线性段获得,另一种是利用机械阻抗法通过测试动载作用下的桥墩基础动刚度来间接推算[1-3]。当测试对象为服役桥梁时,后者是唯一可采用的手段。既有研究大多数只分析了单桩动刚度[4-5],对于常用的群桩-承台基础形式,往往不具备直接在桩顶施加动载的条件,取而代之的是在承台顶部[6]或桥墩顶部施加动载,获得整个群桩-承台-桥墩体系的动刚度。
为了获得群桩-承台-桥墩体系相对稳定的动刚度值,激振点和拾振点均应合理选取。此外,当需要评估一系列桥墩基础的竖向动刚度时,不同桥墩墩高的差异对竖向动刚度的影响也不容忽视。为分析上述问题,本文建立了三维动力有限元模型,施加瞬态激励以分析系统的竖向动刚度值。考虑了激振点分别位于墩顶和承台顶2种情况,分别分析了这2种激励情况下,系统竖向动刚度受墩高变化的影响。
1 桥墩-基础-土层耦合分析模型
利用有限元软件MIDAS/GTS建立了桥墩-基础-土层耦合三维动力分析模型(图1)。土层四周和底部模拟为黏弹性人工边界。桥墩基础形式考虑为4根桩组成的群桩-承台基础,桩径1.2 m,承台尺寸为5.4 m×5.4 m,桥墩截面尺寸为2.4 m×1.8 m,墩身截面不改变,墩高在0~30 m之间变化(墩高为0时即模型中不包括桥墩单元)。在第2,3节中分别在承台表面和桥墩顶部施加瞬态动力荷载,荷载时程和频谱曲线见图2。将距离墩顶中心1,3,5个单元距离的节点定义为墩顶拾振点A1,A3和A5,将承台顶部距离墩底边缘1,3,5个单元距离的节点定义为承台顶部拾振点B1,B3和B5,墩底中心与承台连接处的节点定义为拾振点C(见图3)。

图1 有限元模型整体及局部示意

图2 瞬态激振荷载时程和频谱曲线
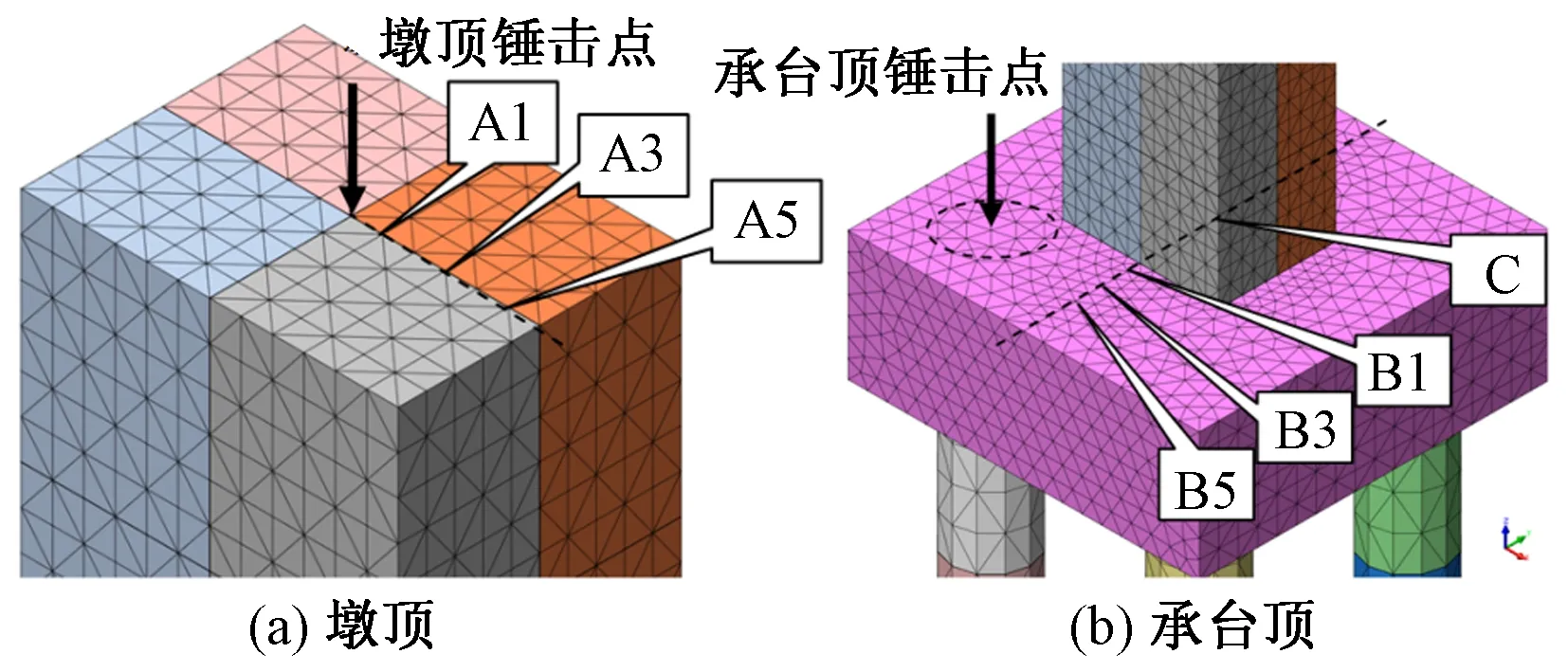
图3 墩顶和承台顶部拾振点示意
机械阻抗法测试中,动刚度函数Kd(f)定义为
(1)
式中:F(f)为激振频谱;v(f)为拾振点速度响应频谱;f为频率;v(f)/F(f)表示速度导纳。
当作用在结构上的动荷载频率f→0时,动刚度值趋于静刚度Ks,即Kd→Ks。激振由于动荷载频率永远大于0,因此动刚度也总是大于静刚度。通常,低频段(<30 Hz)动刚度值相对稳定,对应低频段速度导纳曲线为一斜率恒定的直线[7]。
实际工程测试时,由于激振质量有限等因素,较难得到稳定性较好的10 Hz以下频段动刚度值。研究表明[6]:10~30 Hz动刚度值相对稳定。因此,本文在分析动刚度时,选取2.5 Hz和20 Hz两个代表性频率,前者反映了理想状态下一个较低的频率,后者反映了工程测试中常分析的频率。
2 锤击承台时竖向动刚度分析
2.1 墩高变化对动刚度的影响
当锤击单根桩所对应承台顶部时,承台上拾振点B1动刚度随墩高变化曲线见图4(a)。不同频率下动刚度随墩高变化趋势不同。频率较低时(2.5 Hz),动刚度值相对稳定,但频率较高时(如20 Hz)动刚度变化幅度很大:在墩高从6 m变到9 m时,以及从18 m 变到21 m时,动刚度出现两个增加的突变;其余情况是随墩高增加动刚度减小。
进一步分析承台正中C点的动刚度,其变化规律与B1点不同,见图4(b)。2.5 Hz频率下动刚度值相对稳定,但20 Hz频率下动刚度除0 m到3 m出现一个突变值外,动刚度均随墩高增加缓慢减小。显然,3 m 墩高的动刚度突变与从无墩到有墩应力场突变有关。

图4 锤击承台顶时B1点和C点动刚度随墩高变化曲线
2.2 墩高变化对系统模态的影响
在2.1节中,20 Hz时B1点和C点动刚度随墩高变化表现出完全不同的规律,尽管2个点都位于承台顶面,但其区别在于C点位于体系对称中心,而B1点则不是。由于施加冲击力位于桩顶对应承台上,是一个非对称荷载,因此随着墩高增加,承台模态不对称性出现跳跃性渐变可能会引起上述现象。为了证明这一点,进一步分析墩高在0~30 m范围内变化时,承台和桥墩系统在100 Hz以内的模态情况,见表1。从表1可见,拾振点B1在20 Hz时动刚度发生突变的点(墩高9,21 m 时)都对应有20 Hz频率附近模态阶数的突变:墩高在0~6 m变化时,20 Hz位于第1阶模态之内;墩高为9 m时,20 Hz位于第1,2阶模态之间(动刚度突变);墩高在12~18 m变化时,20 Hz位于第2,3阶模态之间;墩高为21 m时,20 Hz位于第3,4阶模态之间(动刚度突变);墩高在24~30 m变化时,20 Hz位于第4,5阶模态之间。由此可见,当锤击位置不在系统对称点上时,桥墩高度改变对10~30 Hz频率下动刚度影响较大。
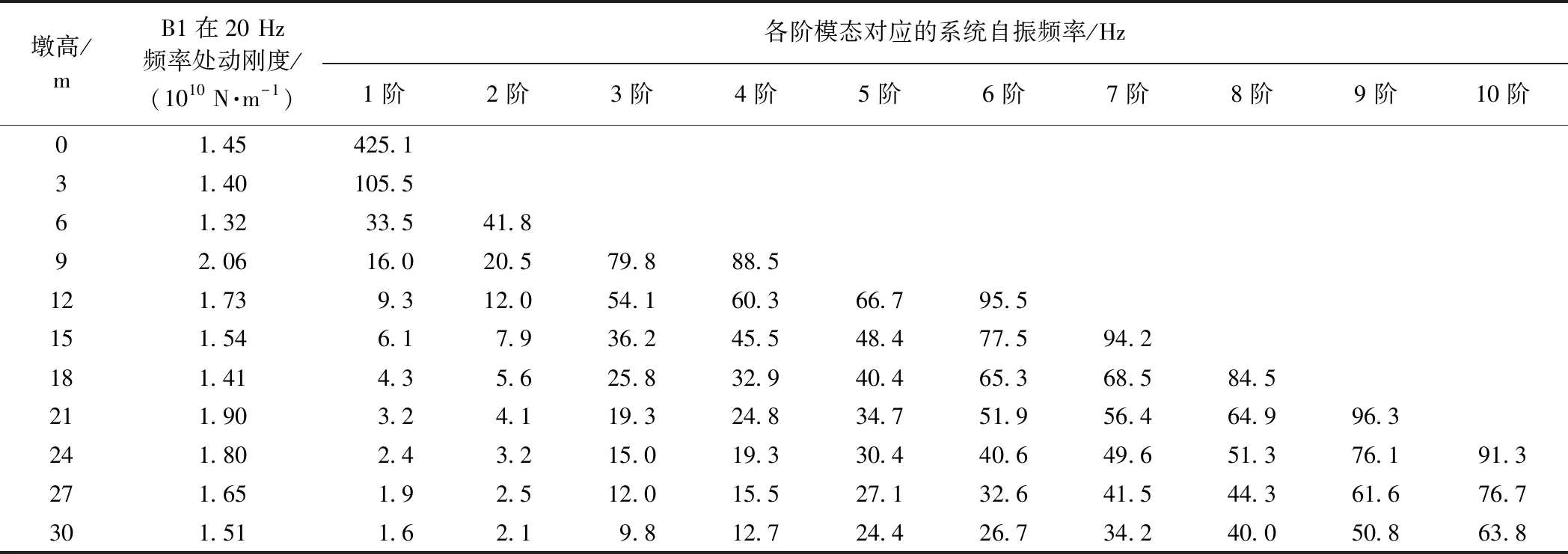
表1 承台-桥墩系统各阶模态自振频率随墩高变化情况
3 锤击墩顶时竖向动刚度分析
当锤击墩顶中心时,墩顶测点A1,A3和A5在2.5 Hz和20 Hz频率下的动刚度随墩高变化曲线见图5。当锤击墩顶中心时,承台顶部测点B1,B3和B5在2.5 Hz和20 Hz频率下的动刚度随墩高变化曲线见图6。可以看出,变化趋势与第2节中锤击承台顶部情况不同:当分析频率极低时,动刚度数值相对稳定,受墩高影响不大;而当分析频率为20 Hz时,动刚度均随墩高增加而单调递减。

图5 锤击墩顶时,墩顶测点A1,A3,A5动刚度随墩高变化曲线
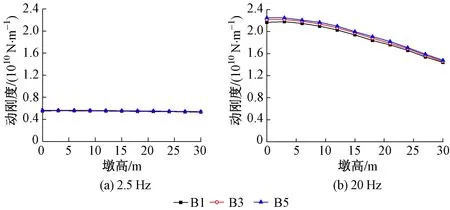
图6 锤击墩顶时,承台顶测点B1,B3和B5动刚度随墩高变化曲线
为进一步对比不同位置处动刚度随墩高变化的衰减梯度,将图5(b)、图6(b)图形绘制在同一张图中分析(图7)。可以发现:墩高小于15 m时,墩顶和承台顶在20 Hz时动刚度的衰减梯度有所差异,且墩高越低,衰减梯度差异越明显。而当墩高大于15 m时,二者衰减梯度趋于一致。

图7 锤击墩顶时,墩顶和承台顶面在20 Hz的动刚度随墩高变化趋势
由此可见,如果通过锤击墩顶获得系统在20 Hz左右的动刚度,墩高的影响不容忽视。当分析一系列桥墩基础动刚度时,如果桥墩墩高差异明显,采用20 Hz 频率下的动刚度较难作为一个合理指标去估算系统的静刚度值。
4 结论与建议
通过建立三维动力有限元模型,分析了桥墩高度对群桩-承台系统动刚度的影响。考虑了激振点位于承台上和桥墩顶部2种情况,计算结果表明:
1)2种激振点位情况下,2.5 Hz频率下系统动刚度受桥墩高度变化影响小,计算结果稳定。
2)当激振点位于承台上时,由于激振点和拾振点均不在结构对称中心上,因此当频率较高时(20 Hz左右),系统动刚度会受到自身模态的影响而发生阶跃式突变。
3)当激振点位于墩顶中心时,随着桥墩高度的增加,20 Hz频率下的系统动刚度降低。
根据计算结果,当工程中需要测试评估一系列群桩基础-承台-桥墩系统的动刚度时,应尽可能取较低的分析频率。当振源无法激励出稳定的低频振动时,建议优先选择墩顶作为激振点,且应考虑墩身高度对结果进行修正。

