基于数据内在特性和LSTM的用电数据异常检测算法研究
吴刚
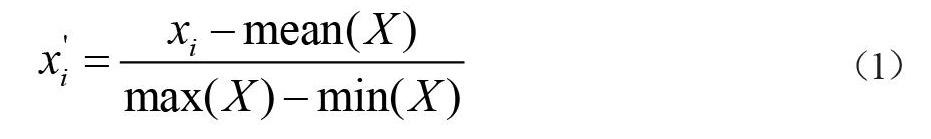

摘 要:为解决现有用电数据异常检测算法准确率低的问题,首先,文章分析了用户用电数据具有时间关联特性、高维度特性,且容易受外部因素影响等特性。其次,基于数据内在特性和LSTM理论,提出了基于数据内在特性和LSTM的用户用电数据异常检测算法。该算法采用有放回的构造数据集策略,构造K个数据集合,采用4层LSTM网络,实现高维数据特征提取,利用两层全连接的隐含层组成的神经网络,实现用户特征数据匹配,采用大概率事件将K个数据集的结果中出现最多的分类作为该节点的分类。通过实验,验证了文章算法比传统算法好,提高了准确率,降低了误报率。
关键词:大数据;异常检测;深度学习;LSTM
1 大数据和人工智能背景下的电力数据采集
随着社会经济快速发展,电力资源在人民群众的日常生活中发挥的作用越来越重要。但是,个别用户为了减少电力资源费用的支出,通过窃电、欺诈等欺骗手段进行偷电,给电力公司造成了严重的经济损失。为解决此问题,电力公司已经采取了较多的措施进行检查和整改,并且取得了一定的效果[1-2]。智能电网技术的快速发展,为用电数据异常分析提供了新的研究手段。在大数据电力设备采集下的用户用电数据更加丰富、数据量更加庞大[3]、存储设备和网络通道的资源更加丰富[4]。例如,史玉良等[5]提出了传统数据库和MongoDB数据库相融合的电力用户数据存储体系架构,实现了电力用户数据的可扩展性存储。
在此背景下,基于大数据和人工智能技术的用电数据异常检测研究已成为当前的研究热点和研究趋势。根据研究采用的工具和方法不同,可以分为以下3类。(1)基于统计学理论知识进行异常用电数据挖掘研究,盛立锃等[6]将多项式拟合技术应用到异常用电数据检测当中,有效地解决了用电量预测效率低的问题。Bianco等[7]分析了用电数据的内在特点和关联关系,将用户用电数据检测问题转换为线性回归问题进行求解,提高了用户用电数据检测的准确率。Pappas等[8]、Wang等[9]分析了时间序列理论和自回归理论,提出了自回归移动模型,有效解决了季节变化对用户用电异常检测产生的负面影响。(2)基于数学建模与专家系统相结合的用电异常检测研究,Arisoy等[10]基于电力公司长期运营的专家知识,对用电数据的时间关联关系进行了数学建模,实现了用户异常用电量的检测,并通过仿真实验,验证了算法提高了检测效率和性能。李亚等[11]将电力数据建模为聚类模型,基于专家知识分析,提出改进K-means聚类和反向传播(Back Propagation,BP)神经网络的台区线损率算法,有效提高了用户用电数据的线损率分类性能。石帮松等[12]从经济学的视角,将电力用户数据建模为博弈模型,从经济学理论方面,研究了用电数据的特性。(3)基于深度学习等人工智能理论进行数据分析。Zhang等[13]、赵文清等[14]基于循环神经网络理论和长短期记忆网络理论,提出基于深度学习的用戶用电数据分析,有效提高了数据分析结果的准确率。许元斌等[15]分析了单一聚类算法在电力用户数据分析时性能低的问题,提出了基于K-means和Canopy的双聚类智能检测算法,并通过实验验证了算法的运行效率。
基于上述分析可知,用户用电数据异常检测研究已经取得了较多研究成果。但是,当前研究主要集中在解决异常用电数据检测的性能方面的问题。随着电力用户数据和用电设备地快速增长,用户用电数据的维度和数据量也快速增加,导致现有用电数据异常检测算法性能低的问题。为解决此问题,本文分析了用户用电数据具有时间关联特性、高维度特性,提出了基于数据内在特性和长短期记忆网络(Long Short-Term Memory,LSTM)的用户用电数据异常检测算法。通过实验,验证了本文算法比传统算法好,提高了算法性能。
2 电力公司目前面临的问题
在大数据环境下,电力公司可以通过网管系统采集和存储的数据类型更加多样,数据保存时间更长。这对于用户用电异常数据检测提供了丰富的数据资源。通过对长时间段内数据的关联关系进行分析可知,不同用户电力数据之间存在相似性,同一用户在不同时间段内的数据也存在相关性。例如,某一个居民在未来几天的用电量与当前时间的用电量类似和相关。居民的用电数据也具有一定的周期性和规律性。例如,每个月的用电数据量与之前月份或往年同期月份具有一定的相关性。此外,用户的用电量与天气、节假日等外部环境关系也比较紧密。
从上述分析可知,在进行用电量分析时,如果能够同时对一个长时间段内的数据进行分析,将有助于通过用户用电量的关联关系,分析用户用电数据之间的时序关系,有效挖掘用户用电的异常数据。本文以378天为时间周期,选取了某省电力用户的用电数据进行异常数据检测。数据信息包括用户ID、年月日、用电量等字段数据。
3 数据准备和优化
3.1 数据预处理
为提高数据质量,减少数据重复和数据缺失等错误导致的检测算法性能低的问题,在执行检测算法之前,对数据进行了预处理。其中,对于重复数据,采取删除策略进行处理。对于缺失数据和错误数据,首先,建立数据字段的上限值和下限值。其次,从上下限区间采用随机选择的办法进行填补。最后,对所有数据字段进行归一化处理,避免不同字段取值范围的区别导致的数据质量问题。归一化处理采用公式(1)进行处理。其中,X={x1,x2,…,xn}表示包含n个数据的向量。mean(X)表示求解X的平均值。max(X)表示X的最大值。min(X)表示X的最小值。X'i表示对Xi执行归一化之后得到的数据。
3.2 生成K个数据集合
随着存储设备和存储技术的丰富和成熟,电力公司存储的用户用电数据量爆发式增长,这些数据资源对用电异常检测提供了丰富的资源。通过对已有的用电异常检测研究分析可知,过拟合问题是一个常见问题。为了减小过拟合问题对检测结果的影响,本文在生成测试集和训练集的过程中,采用有放回的构造数据集的策略,构造K个数据集合,提高数据集合的随机性。在选取K个数据集合之后,将其中90%的数据作为训练集进行训练,将剩余的数据作为测试集进行测试。
如果同时对一个较长时间段内的数据进行分析,需要检测算法具备处理高维数据的能力。针对此问题,下一步将基于LSTM理论,提出能解决高维数据的异常数据检测算法。充分挖掘隐含在高维数据中的关键特征,挖掘出的关键特征越多,检测算法的检测性能越好,将越有利于提出更加优化的检测算法。
4 基于数据内在特性和LSTM的用电数据异常检测算法
4.1 算法流程
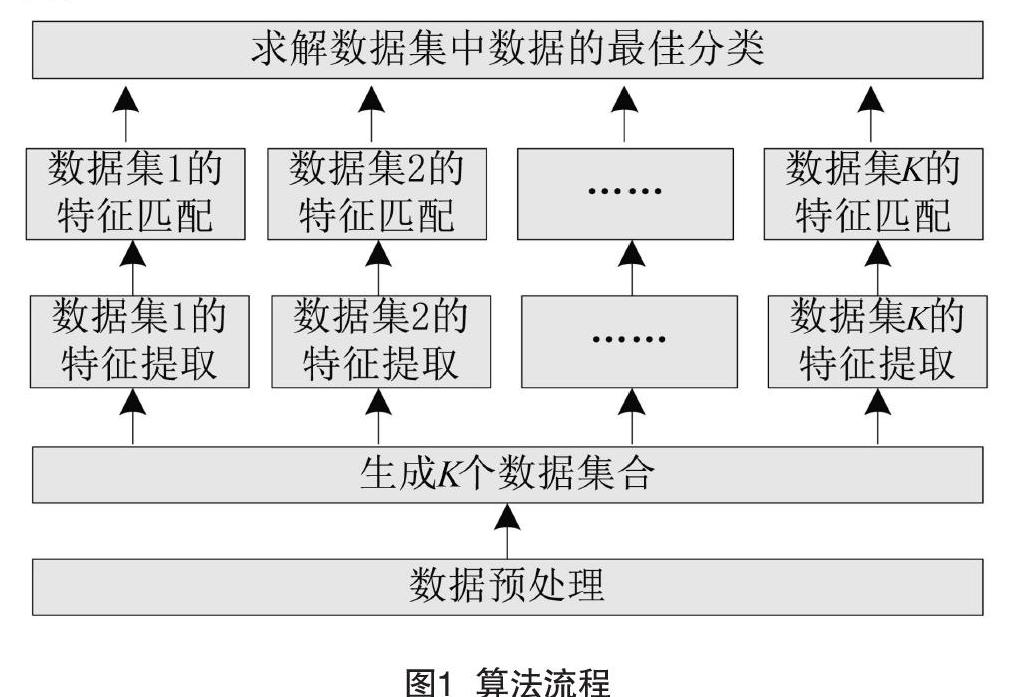
基于数据内在特性和LSTM的用电数据异常检测算法流程如图1所示,包括5个过程。
(1)数据预处理:对于重复数据、缺失数据和错误数据进行清洗,采用归一化处理方法,对数据实现归一化处理。
(2)生成K个数据集合:采用有放回的构造数据集的策略,构造K个数据集合,提高数据集合的随机性。
(3)对K个数据集进行特征提取:对于每个数据集,基于用电特性的4层LSTM算法,从378个特征中提取32个数据的内在关键特征。
(4)对K个数据集进行特征匹配:对于每个数据集,采用3层全连接层进行窃电识别,直到损失函数达到阈值,输出2维的数据分布。
(5)求解数据集中数据的最佳分类:采用大概率事件,将K个数据集的结果中出现最多的分类作为该节点的分类。
4.2 特征提取
由于LSTM网络具备记忆功能,可基于时间关系关联电力用户数据,本文的特征提取模块由多个长短期记忆块连接组成,其结构如图2所示。首先,将第K个数据集合划分为3个数据子集作为输入。其次,4层LSTM构成的特征提取模型对特征进行提取。
从用电特性角度分析可知,用电与温度、节假日影响较大,考虑到春、夏、秋、冬4个季节,清明节、中秋节、端午节、元旦、五一、国庆节、春节7个关键节日,所以,本文在4层LSTM网络实现特征提取时,将用电特征设置为32。对于每个LSTM网络模块,包括输入门、遗忘门、输出门3种门。其中,输入门用于接收用户用电数据xt和上一个时刻的输出ht-1,输入值z使用公式tanh(Wz[ht-1,xt])计算。输入门的取值i使用sigmoid(Wt[ht-1,xt])进行计算。遗忘门的取值f使用公式sigmoid(Wf[ht-1,xt])进行计算。输出门的取值o使用公式sigmoid(Wo[ht-1,xt])进行计算。基于此,LSTM网络模块的新状态取值ct使用公式(2)进行计算,每个LSTM网络模块的输出值ht使用公式(3)进行计算。
4.3 特征匹配
为完成数据类型的标注,本文利用一个由2层全连接的隐含层组成的神经网络实现用户特征数据的匹配工作。该特征匹配模型中,输入层输入数据为特征提取获得的32维数据。为提高算法的性能,本文使用均方差损失函数,对神经网络的参数进行调整。均方差损失函数使用公式(4)进行计算。其中,yi表示特征匹配模块的分類结果,表示用户用电数据的真实分类结果,N表示特征匹配模块分类的用电数据的数量。
4.4 求解数据集中数据的最佳分类
考虑到K个数据集的特征配匹结果存在差异,不便于决定最优的分类结果。本文基于随机森林算法求解数据最佳分类的方法,最终的分类结果采用概率事件进行计算,即对于每个用电用户数据,将K个特征配匹结果中相同分类最多的类型作为最终的分类。
5 性能分析
为了生成数据集,本文选取某省95 389个用电用户的378天的电量数据,其中,异常数据3 528条,其余为正常数据。本文算法中K取值为[3,9],步长为2。在进行实验时,为了防止正常数据和异常数据不均衡影响算法性能,在构造训练数据时,对正常数据进行欠采样,减小正常数据与异常数据的不均衡差距。实验中,共生成10个数据集,每个数据集进行10次实验,最终结果取平均值。
实验中,首先,分析了K取值对算法性能的影响。其次,为了验证本文所提模型的有效性,与传统的机器学习算法支持向量机(ADoSVM)、使用单个数据集合算法(ADoIL-oneD)进行对比实验。
首先,K取值为3,5,7,9时算法性能如图3—4所示。随着K取值增加,算法的准确率逐渐增加,误报率逐渐降低。当K取值为9时,算法性能出现下降。实验结果说明,K取值为7时,算法性能比较优化。
下面以K取值为7的情况下,与传统的机器学习算法支持向量机(ADoSVM)、使用单个数据集合算法(ADoIL-oneD)进行对比实验。算法性能如图5—6所示。算法ADoIL-7和算法ADoIL-oneD两种算法的准确率都高于算法ADoSVM,误报率都低于算法ADoSVM,说明本文算法提出的异常检测算法优于传统的机器学习算法。另外,算法ADoIL-7的性能优于算法ADoIL-oneD,说明多数据集减小了过拟合问题对算法性能的影响,有助于求解最佳的分类结果,提高了异常检测算法的检测性能。
6 结语
电力资源在人民群众的日常生活中发挥的作用越来越重要。但是以窃电、欺诈等欺骗手段进行的偷电行为给电力公司造成了严重的经济损失。用户用电数据异常检测研究对于电力公司的正常运营变得更加重要。为解决此问题,本文分析了用户用电数据具有时间关联特性、高维度特性,提出了基于数据内在特性和LSTM的用户用电数据异常检测算法。通过实验,验证了本文算法比传统算法提高了算法性能。下一步工作中,将对该模型进行优化,基于迁移学习理论,生成通用性较强的模型,降低模型对运算环境的要求,提高算法的实用性。
[参考文献]
[1]雷煜卿,李建岐,侯宝素.面向智能电网的配用电通信网络研究[J].电网技术,2011(12):14-19.
[2]ULUDAG S,LUI K S,REN W,et al.Secure and scalable data collection with time minimization in the smart grid[J].IEEE Transactions on Smart Grid,2016(1):43-54.
[3]屈志坚,陈阁.容错存储的电力系统监测数据查询优化技术[J].电网技术,2015(11):3221-3227.
[4]葛磊蛟,王守相,瞿海妮.配用电大数据存储架构设计[J].电力自动化设备,2016(6):194-202.
[5]史玉良,王相伟,梁波,等.基于MongoDB的前置通信平台大數据存储机制[J].电网技术,2015(11):3176-3181.
[6]盛立锃,曾喆昭,李莎.基于代数多项式模型的用电量预测研究[J].电力科学与技术学报,2015(1):34-40.
[7]BIANCO V,MANCA O,NARDINI S.Linear regression models to forecast electricity consumption in Italy[J].Energy Sources Part B Economics Planning&Policy,2013(1):86-93.
[8]PAPPAS S S,EKONOMOU L,KARAMOUSANTAS D C,et al.Electricity demand loads modeling using Auto Regressive Moving Average(ARMA)models[J].Energy,2008(9):1353-1360.
[9]WANG Y,WANG J,ZHAO G,et al.Application of residual modification approach in seasonal ARIMA for electricity demand forecasting:a case study of China[J].Energy Policy,2012(3):284-294.
[10]ARISOY I,OZTURK I.Estimating industrial and residential electricity demand in turkey:a time varying parameter approach[J].Energy,2014(4):959-964.
[11]李亚,刘丽平,李柏青,等.基于改进K-means聚类和BP神经网络的台区线损率计算方法[J].中国电机工程学报,2016(17):4543-4551.
[12]石帮松,张靖,何宇,等.基于动态博弈的配电网单相电力用户用电行为分析[J].电力系统自动化,2017(14):87-91,139.
[13]ZHANG J,ZHENG Y,QI D.Deep spatio-temporal residual networks for citywide crowd flows prediction[J].AAAI,2016(5):25-29.
[14]赵文清,沈哲吉,李刚.基于深度学习的用户异常用电模式检测[J].电力自动化设备,2018(9):34-38.
[15]许元斌,李国辉,郭昆,等.基于改进的并行K-means算法的电力负荷聚类研究[J].计算机工程与应用,2017(17):260-265.

