抽汽供热机组自整调节控制策略研究
姜清尘,有志伟,杨建明
(1.东南大学 能源与环境学院,南京 210096;2.上海电气电站设备有限公司 汽轮机厂,上海 200240)
“十三五”规划以来,热电联产规模进一步扩大,大容量、高参数、双级抽汽供热机组大量投运。但受制于热、电负荷间复杂的耦合关系,目前行业内抽汽供热机组的自整调节策略尚不完善[1]。部分热电厂的调节过程主要依赖于操作人员的经验,在保证热功率稳定的前提下缓慢改变各个阀门的开度来实现对电功率的调节。这种控制方式调节时间长,热电过程的调整缓慢并且不准确,难以达到电网要求的一次调频考核标准。
早期的机械液压调节系统多基于线性机理模型,通过优化调节阀的结构设计,使调节阀传递矩阵和调节对象传递矩阵相乘得到对角矩阵来消除热电负荷的耦合关系[2]。随着数字电液调节系统的出现,控制回路中加入了关于电功率及供热蒸汽抽汽压力PI调节器的负反馈调节[3]。传统调节方式对非再热单级抽汽供热机组这一类结构简单的供热机组具有良好的适用性,但对于结构日益复杂的供热机组,控制效果不佳,易导致油动机长期处于波动中,出现漏油磨损等情况。究其原因,在于控制算法中对抽汽供热机组这一被控对象的运行特性仍缺乏深入的研究。
笔者提出了一种以热工况图为核心,基于抽汽供热机组热力特性及调节阀特性的自整调节控制策略,并以CC100-8.83/4.12/1.47型100 MW双级抽汽供热凝汽式汽轮机为研究对象,在基于LabVIEW软件平台建立的动态仿真模型上,进行单级、双级抽汽供热变工况试验,验证了该自整调节策略的可行性。
1 热力系统
1.1 系统简述
抽汽凝汽式供热机组热力系统由锅炉、汽轮机、发电机、凝汽器、高压加热器、低压加热器、除氧器、给水泵、凝水泵等设备组成。以某单级抽汽供热机组为例,其原则性热力系统见图1。
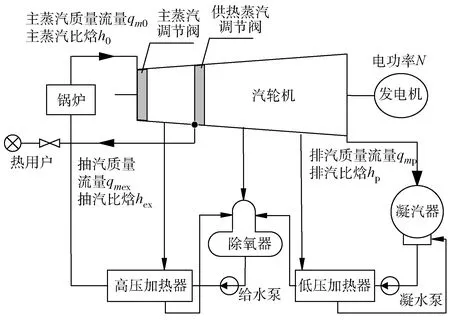
图1 抽汽供热机组热力系统图
1.2 热电耦合关系
供热机组对外输出热、电两类负荷。以图1的抽汽供热机组为例,若忽略小流量的非调整抽汽,则电功率及抽汽质量流量可用式(1)表示:
(1)
式中:N为电功率,kW;qm0为主蒸汽质量流量,kg/s;h0为主蒸汽比焓,kJ/kg;qmex为抽汽质量流量,kg/s;hex为抽汽比焓,kJ/kg;qmp为排汽质量流量,kg/s;hp为排汽比焓,kJ/kg。
经简单推导,该机组热电关系见式(2),qmex的改变会使N随之变化。在供热机组调节过程中,主蒸汽调节阀开度XC0或供热调节阀开度XCi(i=1或2)中任意一者的单独变化都会同时影响N和qmex,这一特性称为热电耦合。耦合关系也可用矩阵形式表示,单级抽汽供热机组热电耦合关系见式(3),双级抽汽供热机组见式(4)。
N=qm0×(h0-hp)-qmex×(hex-hp)
(2)
(3)
(4)
式中:耦合矩阵A由机组自身热力特性、调节阀流量特性决定。结构越为复杂的机组,其耦合矩阵越复杂,但对于每一台确定的机组,耦合矩阵是唯一确定的。
2 自整调节控制策略
2.1 策略简述
根据第1.2节所述,抽汽供热机组自整调节的本质即求解热电耦合矩阵A的逆矩阵A-1。A和A-1的求解可以根据机组热力特性和调节阀流量特性分别构建数学模型,将解耦过程拆分为两步:先以电网和热用户所需的热电负荷N、qmex为输入值,根据机组热力特性计算出所需的主蒸汽及供热蒸汽调节阀的通流质量流量qmC0、qmCi,以矩阵形式表示[见式(5)],矩阵B即热蒸汽调节阀通流质量流量与热电负荷之间的对应关系;再以调节阀通流质量流量为输入值,根据调节阀流量特性计算出通过相应流量所需的开度指令XC0、XCi(i=1或2),以矩阵形式表示[见式(6)],矩阵C即调节阀开度与调节阀通流量之间的对应关系。
上述过程相当于将热电耦合矩阵的逆矩阵A-1分解成了两个子矩阵的乘积并分别求解,从本质上完成了热电解耦。
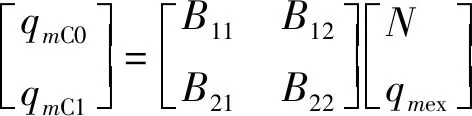
(5)

(6)
联立得:
(7)
则解耦矩阵:
(8)
根据以上分析,得到了基于机组运行特性的自整调节控制策略中的前馈部分。该部分由两步骤组成,分别对应控制算法中的热工况图计算程序和调节阀开度计算程序。
2.2 热工况图计算程序
热工况图反映了抽汽供热机组qm0、qmex与N三者之间的关系,是供热机组热力特性的直接体现。关于热工况图的绘制方法,行业内已有明确的规定[4]。热工况图同时还包含以下边界条件:最大供热量边界线、最大电功率边界线、最大主蒸汽量边界线、最小排汽量边界线及最小供热量边界线。
单级抽汽供热机组热工况图见图2,双级抽汽供热机组热工况图见图3。
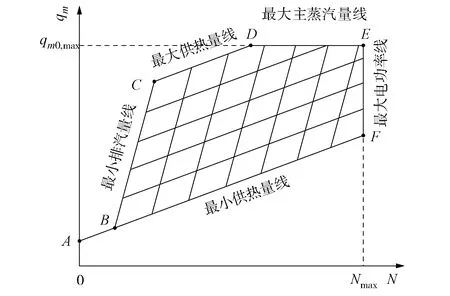
图2 单级抽汽供热机组热工况图

图3 双级抽汽供热机组热工况图
依据热工况图,即可编制相应的计算程序,以N和qmex为输出值,计算qm0。近似认为等供热量线为一组平行的直线,则单级抽汽供热机组qm0计算式为:
(9)
式中:k为一次项系数;b为常数项,是关于qmex的函数F(qmex),可根据实际机组热工况图拟合确定。
对于双级抽汽供热机组,可近似认为当qm0、高压供热量qmex1一定时,随着低压供热量增大,单位低压供热量qmex2所导致的电功率减少量为定值。则qm0计算式为:
(10)
式中:N′可理解为某供热工况下,若低压供热的蒸汽全部返回汽轮机中做功时汽轮机的电功率;k2为一次项系数;k1为单位低压供热蒸汽若用于汽轮机做功能够增加的发电量。
根据qm0和qmex,即可得到各调节阀的qmCi。
2.3 调节阀开度计算程序
调节阀开度计算程序的作用为:以调节阀前的设计压力pV0和第2.2节计算出的调节阀通流质量流量qmV为输入值,计算相应的调节阀开度指令XV。
火电机组汽轮机配汽主要有节流配汽和喷嘴配汽两种方式。节流配汽机组采用全周进汽,将蒸汽通过一个或一组同时启闭的调节阀调节[见图4(a)];喷嘴配汽机组通过调节级调节,调节级由3个以上顺序开启的调节阀及对应喷嘴组组成[见图4(b)]。

图4 火电机组汽轮机配汽方式
无论机组采用何种配汽方式,qmV均可视为关于pV0、XV和调节阀后压力pV1三者的函数。工程计算中,通常忽略pV1变化的影响,认为qmV仅由pV0和XV决定,表达式为:
qmV=F(pV0,XV)
(11)
根据调节阀或调节级流量特性曲线(见图5),可以编制当pV0恒为设计值pV0R时,调节阀质量流量qmVR关于XV的关系式(12)。当变工况下pV0偏离设计值时,可根据pV0与设计压力的比值对调节阀流量进行修正,见式(13)。

图5 主调节级流量特性曲线
(12)
(13)
式中:qmV为调节机构通流质量流量,kg/s;XV为调节阀开度,%;pV0为调节阀前压力,kPa;qmVR为当调节阀前压力为设计压力时的调节阀通流质量流量,kg/s;pV0R为调节阀前压力的设计值,kPa,对于确定的机组,pV0R为确定值(主蒸汽调节级前压力即新蒸汽压力;供热调节级前设计压力即供热压力)。
对式(12)取逆运算,并与式(13)联立,即可得到根据qmV、pV0逆算XV的表达式(14)。式(11)~式(14)即为调节阀开度计算程序的编制依据。
(14)
3 对调节偏差的反馈补偿
3.1 反馈补偿原因分析
第2章所述的自整调节属于开环控制,其控制精度与机组运行方式、热工况图的准确性、调节阀流量特性曲线的准确性、热平衡图的准确性等诸多因素有关。此外,实际机组长期运行过程中,又存在调节阀磨损、通流级组效率变化、结构改造等情况。因此,以上过程所产生的系统误差和偶然误差都将导致计算得到的调节阀开度指令与实际需求值存在偏差。
为补偿这一偏差,自整调节系统引入负反馈控制。以供热蒸汽抽汽压力和机组实际发电功率为被控量,通过串联PI调节器,实现对功率和供热蒸汽抽汽压力的无差调节。
3.2 带偏差死区的PI控制
单级抽汽供热机组控制方框图见图6,双级抽汽供热机组控制方框图见图7。
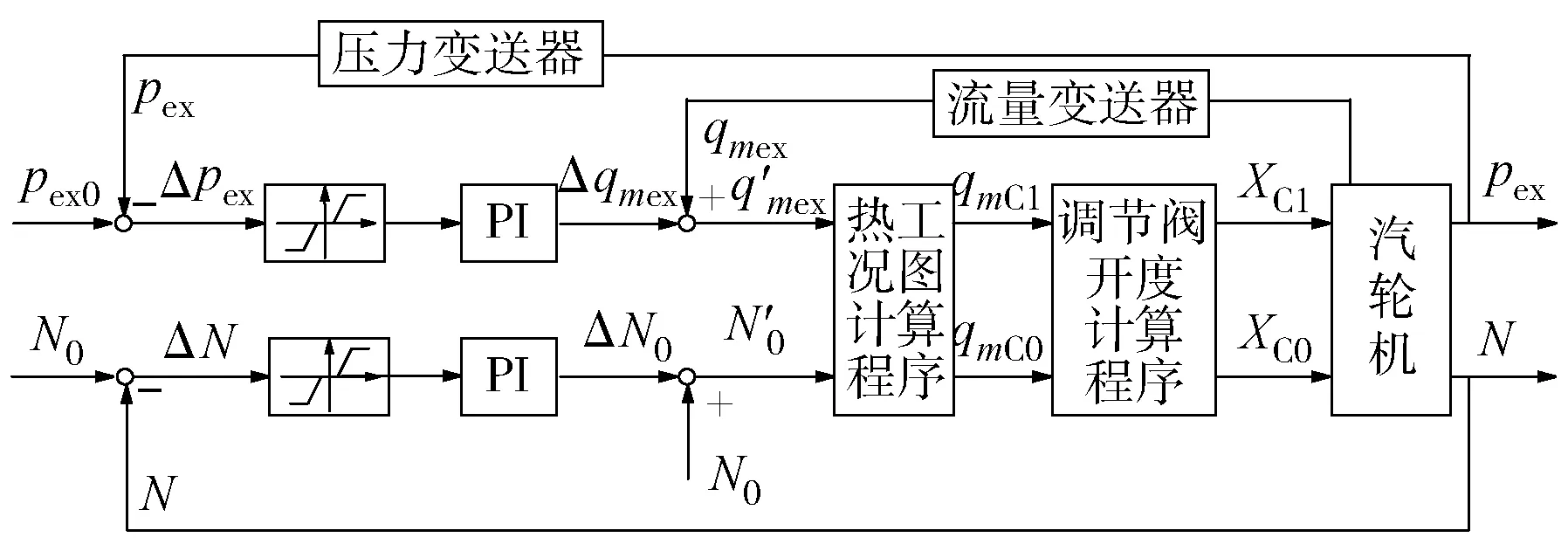
图6 单级抽汽供热机组控制方框图

图7 双级抽汽供热机组控制方框图
压力变送器和流量变送器分别测量pex和qmex。控制程序根据机组实际电功率与电网指令偏差ΔN及供热蒸汽抽汽压力与设计压力偏差Δpex,通过PI调节器,对机组qmex和目标电功率N0进行修正。修正后的qmex′和N0′作为输入值,送入热工况图计算程序和调节阀开度计算程序,即可计算所需的调节阀开度X。
所述负反馈调节系统带有偏差死区功能,当pex、N与目标值的偏差在允许范围以内时,偏差输出为0,此时调节阀不再动作,有利于减小油动机的磨损,并提升调节过程的稳定性。
4 仿真结果与分析
4.1 研究对象简述
以CC100-8.83/4.12/1.47型100 MW双级抽汽供热凝汽式汽轮机为研究对象,其原则性热力系统图见图8。该机组采用定压运行,通过控制主蒸汽调节级C0开度调整主蒸汽流量。供热工况下,高、低压热用户分别通过改变高、低压供热阀开度X1、X2调节供热蒸汽流量。机组自整调节系统通过控制高压供热调节级C1开度以维持高压供热蒸汽抽汽点A压力为4.12 MPa,通过控制低压供热调节级C2开度以维持低压供热蒸汽抽汽点B压力为1.47 MPa。
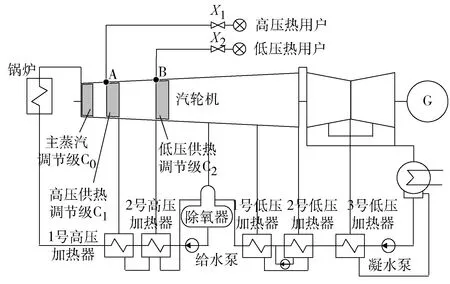
图8 CC100-8.83/4.12/1.47机组原则性热力系统图
基于LabVIEW软件平台建立汽轮机侧动态仿真数学模型。在仿真模型基础上,按第2、第3章所述的解耦策略建立自整调节控制程序,并进行单级、双级抽汽变工况试验。
4.2 单级抽汽供热变工况试验
以高压单级抽汽供热试验为例,手动改变供热阀开度X1以模拟高压热用户用汽量变化,手动改变N0以模拟电网负荷指令变化。自整调节系统通过调节C0及C1开度以响应电负荷需求,并维持高压供热蒸汽抽汽点A压力4.12 MPa。X1开度扰动、N0扰动试验见表1,电功率及高压供热蒸汽压力动态响应曲线见图9。

表1 高压单级抽汽供热变工况试验



图9 高压单级抽汽供热变工况试验1、2动态曲线
由表1可以看出:在所设计的自整调节控制算法下,机组电功率静态偏差在1%以内,供热压力静态偏差在0.5%以内,且调节过程动态响应良好。
4.3 双级抽汽供热变工况试验
双级抽汽供热工况下,手动改变供热阀开度X1、X2以模拟高、低压热用户用汽量变化,手动改变N0以模拟电网负荷指令变化。自整调节系统通过调节C0、C1、C2开度以响应电负荷需求,并维持高压供热蒸汽抽汽点A压力4.12 MPa,低压供热蒸汽抽汽点B压力1.47 MPa。X1、X2开度扰动和N0扰动试验见表2,电功率及高、低压供热蒸汽压力动态响应曲线见图10。

表2 双级抽汽供热变工况试验
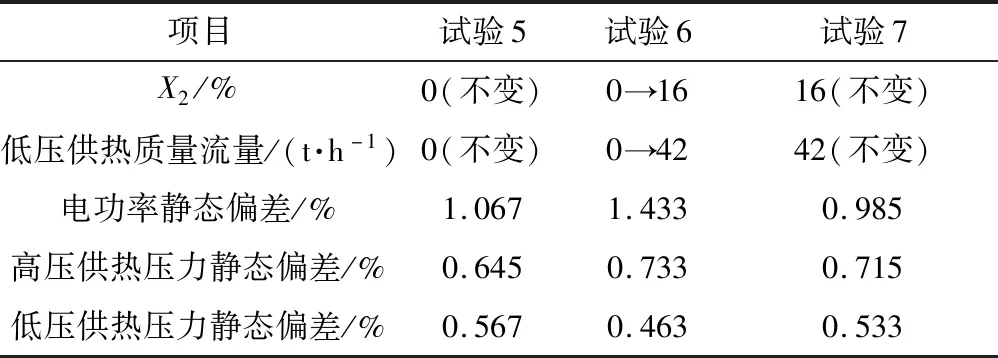
表2(续)

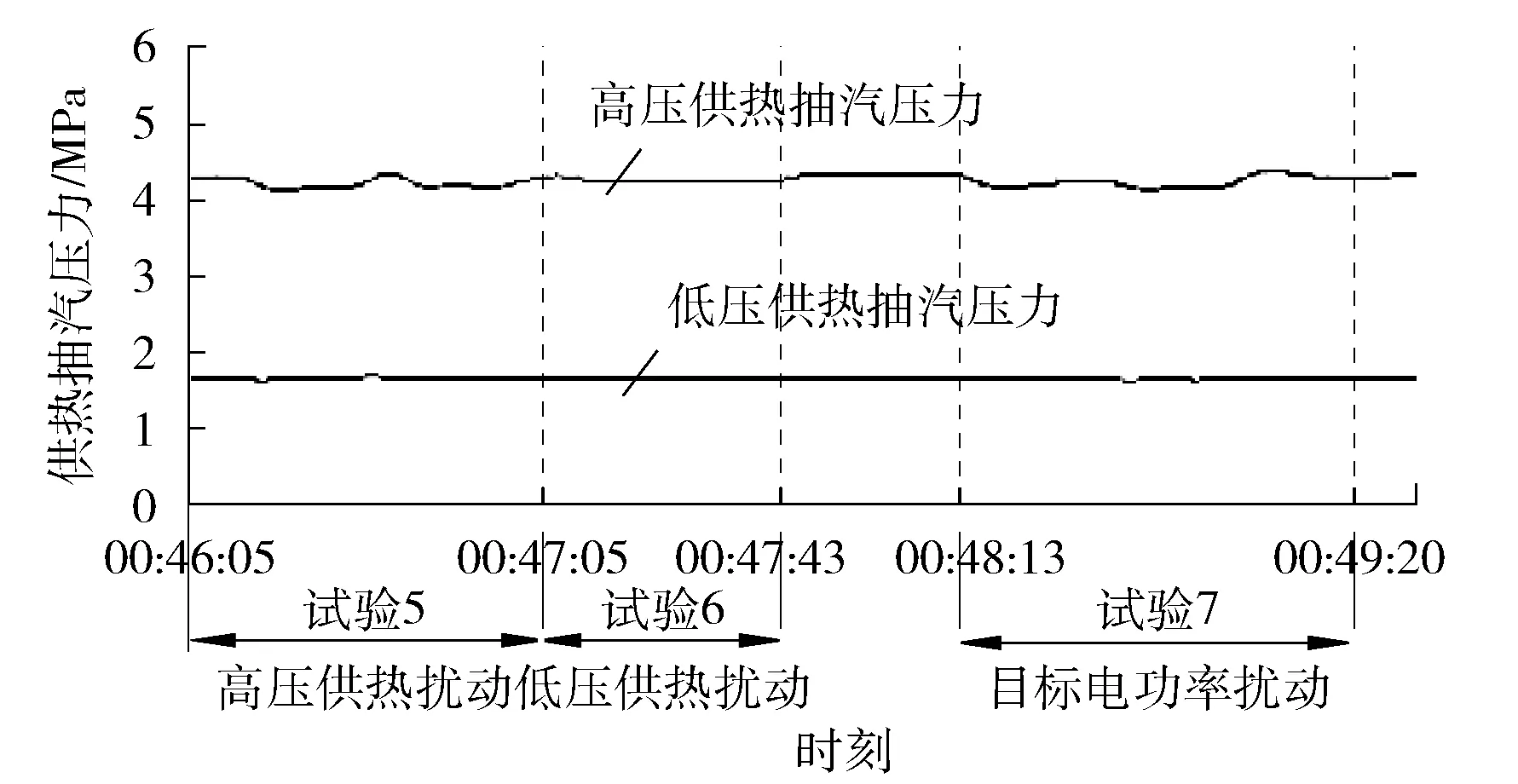
图10 双级抽汽供热变工况试验5、6、7动态曲线
由表2可以看出:在所设计的自整调节控制算法下,机组电功率静态偏差在1.5%以内,供热压力静态偏差在1%以内,且调节过程动态响应良好。
5 结语
(1)笔者提出了一种以热工况图为核心,基于抽汽供热机组运行特性的自整调节控制策略。通过建立抽汽供热机组动态数学模型,并进行电功率目标值扰动及供热量扰动等变工况试验,验证了这种自整调节策略的可行性。
(2)相比于传统的调节方案,该调节策略的优势为:将具体机组的热力特性(热工况图)及调节阀特性(调节阀流量曲线)纳入自整调节算法中作为前馈调节,可以有效提升一次调节的准确性,减少后续负反馈调节的时间,从而在保证调节精确性的同时能有效减少油动机的磨损。
(3)该调节策略尚存在一些问题:工程实际中通常只监测供热蒸汽抽汽的压力,而不直接监测供热质量流量,因此如果要应用这种控制策略,则应增加流量变送器;且热工况图和调节阀流量曲线的录入会使控制系统相对复杂。但是随着计算机运算能力的提升与传感器工艺的发展,这种自整调节控制策略作为一种新的、可行的控制思路,具有进一步研究的意义和价值。

