含腐蚀缺陷埋地管道悬空段力学作用与可靠性分析

王晓静,倪晓阳,李明桥

(1.中国地质大学(武汉)工程学院，湖北 武汉 430074；2.湖北省汉江河道管理局,湖北 潜江 433100)

近年来，我国长输油气管线铺设规模大幅提升，油气管道长期服役后，会因外部干扰、腐蚀、管材和施工质量等缺陷发生失效事故，其中埋地管道意外悬空是管道安全事故的常见失效形式。为了保证管道的安全，许多学者对含腐蚀缺陷的埋地管道进行了研究。如杨理践等[1]针对管道的腐蚀缺陷，给出了它们适用的缺陷尺寸范围；顾晓婷等[2]研究认为针对中低强度管线钢在选用剩余强度评价方法时可选择改进的B31G方法，而针对中高强度管线钢在选用剩余强度评价方法时可选用DNV RP-F101和

PCORRC方法；马廷霞[3]综合了前人的研究方法，建立了埋地管道悬空段的几何非线性大变形分析模型。

基于上述研究，本文采用有限元分析软件Abaqus，对含腐蚀缺陷的埋地管道悬空段受力情况与可靠性进行了数值模拟研究。

1 埋地管道悬空段受力有限元分析模型的建立

本文选择直径为610 mm、壁厚为8 mm、内压为4.3 MPa的X65管线钢为研究对象,根据《油气输送管道穿越工程设计规范》的要求，埋地管道在实际铺设的过程中，管道埋深一般为1～3 m,考虑到埋地管道悬空段管-土相互作用的区域可以无限延伸，在有限元仿真模拟中为了便于计算分析，将土体模型的宽度和深度设置为10 m。

1. 1 材料参数的选择

X65管线钢和土体材料的各项物理参数见表1和表2[4]，以便对管道和土体的材料属性进行设置。

表1 X65管线钢材料的物理参数

表2 土体材料的物理参数

在Abaqus软件中，选用摩尔库仑模型对土体进行模拟分析，符合基于温克乐地基假设的弹塑性地基模型，该模型所需的相关数据可以通过试验获得。黏土材料的各项性能参数见表3。

表3 黏土材料的性能参数

Ramberg-Osgood本构关系[3]能够较为准确地反映材料应力与应变的弹塑性关系。根据X65管线钢的本构关系和管材的各项物理参数，对管道材料属性进行设置。X65管线钢材料应力与塑性应变对应的关系数据见表4。

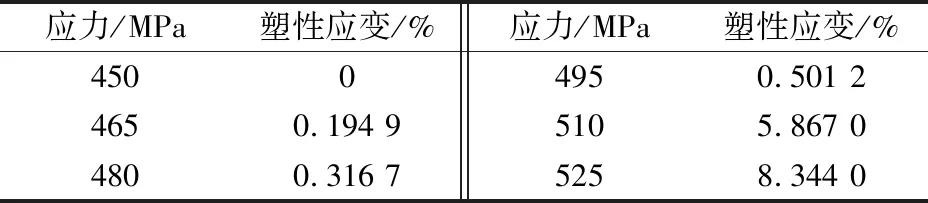
表4 X65管线钢材料应力与塑性应变对应的关系数据

1. 2 单元选择与网格划分

由于埋地管道悬空段的静力学分析需要考虑土体的弹塑性变形，所以在土体单元的选择中，采用8节点线性减缩单元。在管道单元的选择中，采用三维4节点减缩壳单元。在选择好单元类型之后，对所建立的埋地管道悬空段受力有限元分析模型进行网格划分，通常对重点研究区域的网格加密，而对非重点研究区域的网格划分得较稀疏，其网格划分结果见图1。

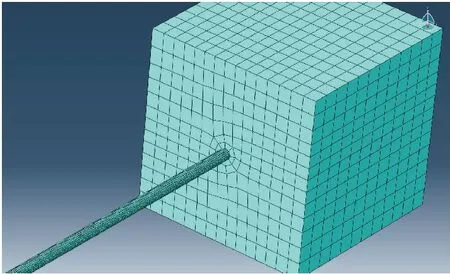
图1 网格划分局部图Fig.1 Local grid division diagram

1. 3 管-土相互作用与边界条件设置

考虑到埋地管道悬空段力学模型中的管-土相互作用，在对管-土接触端的表面设置接触时，将管道与土体接触方式设置为表面-表面接触。其中，管道外表面刚度大，设置为主表面；而土体内表面刚度小，设置为从表面。

接触基础属性的设置时，法向行为设置为“硬接触”，管-土接触后允许分离。切向接触考虑土体对管道的摩擦作用，采用“罚”函数定义，设置为库仑摩擦，其具体数值可通过试验获得，查阅文献后取0.5,对土体和管道模型进行对称设置[5]。在约束方面，设置土体4个侧面和底表面为全约束，上表面和内表面为无约束，管体两端为全约束。载荷约束见图2。

图2 载荷约束1/2图Fig.2 Load constraint 1/2 diagram

1. 4 分析步与载荷设置

在埋地管道悬空段的力学模型研究中，埋地管道悬空段所受的载荷主要来源于两个方面：一方面是由管道和运输物质的自重产生；另一方面是由管道内运输物质的内压产生。因此，在载荷设置中，先对整个模型设置重力载荷为9.8 m/s2，再对埋地管道悬空段设置内部压强为10 MPa；然后设置内压载荷和重力载荷两个分析步，增量步数值根据具体情况进行设置。

2 裸露和未裸露的埋地管道悬空段受力情况有限元分析

2.1 裸露的埋地管道悬空段应力和应变失效分析

裸露的埋地悬空管道示意图见图3。

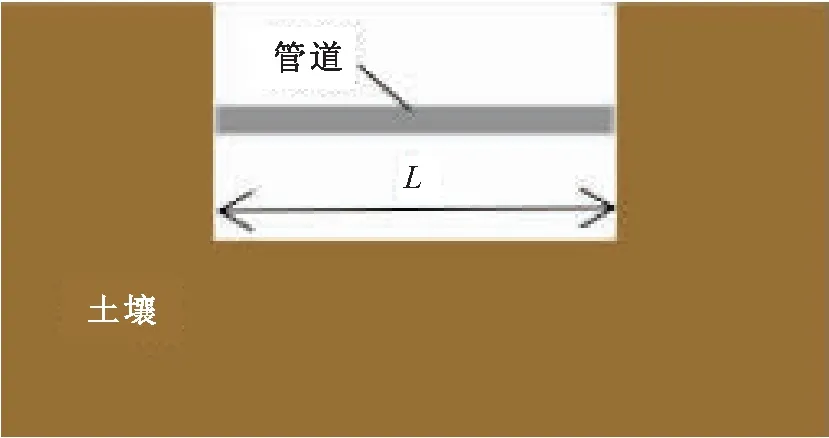
图3 裸露的埋地悬空管道示意图Fig.3 Schematic diagram of the exposed buried suspended pipeline

本文利用Abaqus有限元分析软件,对裸露的埋地管道悬空段的受力情况进行了有限元模拟，模拟得到不同悬空长度下(悬空长度L分别为80 m、130 m、180 m)裸露的埋地管道的应力、应变和中端位移云图。

以此可以得出结论：对于管线钢X65油气管道，其等效应力极大值和等效应变极大值均集中在管-土接触端上表面，而垂直位移极大值则发生在管道的中端，管道悬空长度越大，其极大值越大，且管道悬空长度对垂直位移的影响程度比对应力和应变的影响程度低。

将多组数值模拟所得数据进行拟合，得到裸露的埋地管道最大Mises应力与悬空长度的关系图，见图4。

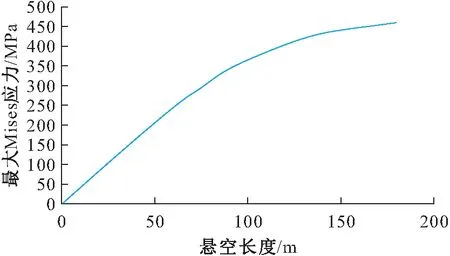
图4 裸露的埋地管道最大Mises应力与悬空长度的 关系图Fig.4 Relationship between maximum Mises stress and suspension length of the exposed buried pipeline

管道材料的最大许用应力为钢材屈服强度的72%，X65管线钢屈服强度为450 MPa，因此其最大许用应力为324 MPa。由图4可见，当裸露的埋地管道的悬空长度为83 m时，管-土接触端上表面的等效应力极大值开始超过管道材料的最大许用应力324 MPa,即管道此时的悬空长度为允许使用的最大安全悬空长度；当裸露的埋地管道的悬空长度为170 m时，管-土接触端上表面的等效应力极大值开始超过管道材料的屈服强度450 MPa，即管道此时的悬空长度为允许使用的极限悬空长度；之后管材开始进入塑性变形时期，管道上的应力随悬空长度的变化开始变得缓慢。因此，基于应力的失效判据，管道的极限悬空长度为170 m左右。

将多组数值模拟所得数据进行拟合，得到裸露的埋地管道最大应变与悬空长度的关系图，见图5。

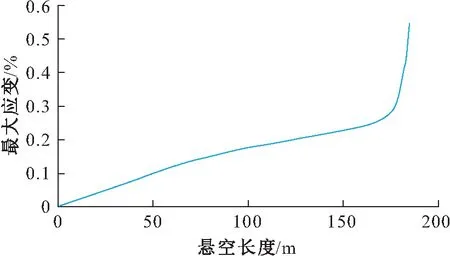
图5 裸露的埋地管道最大应变与悬空长度的关系图Fig.5 Relationship between maximum strain and suspension length of the exposed buried pipeline

当管道所受的应力低于管道屈服强度时，管道最大应变随悬空长度的增加缓慢增大，而当管道所受的应力超过管道屈服强度时，管道最大应变随悬空长度的增加而急剧增大。结合相关文献，将管道最大应变达到0.3%时的悬空长度作为管道安全悬空长度，将管道最大应变达到0.525%时的悬空长度作为管道极限悬空长度[6]。由图5可见，当裸露的埋地管道悬空长度为177 m时，管道达到其最大安全悬空长度；当裸露的埋地管道悬空长度为185 m时，管-土接触端上表面的等效应变极大值开始超过管道材料的最大应变0.3%，即管道此时的悬空长度为允许使用的极限悬空长度。因此，基于应变的失效判据，裸露的埋地管道的极限悬空长度为185 m左右。

2.2 未裸露的埋地管道悬空段应力和应变失效分析

在相同悬空长度下,未裸露的埋地管道的轴向组合应力大于裸露的埋地悬空管道,更易发生失效破坏[7]。未裸露的埋地悬空管道示意图见图6。

图6 未裸露的埋地悬空管道示意图Fig.6 Schematic diagram of non-exposed buried suspended pipeline

取未裸露的埋地管道悬空段的受力截面(见图7)进行分析，可见未裸露的埋地管道悬空段所受的载荷还需加上管道上表面所覆盖土体的重量Q，Q的大小与管道埋深d有关，其计算公式如下：

(1)

式中：Q为土体的重量(N)；L为管道悬空段的长度(m)；D为管径(m);d为管道埋深(m);ρs为土体密度(kg/m3)。

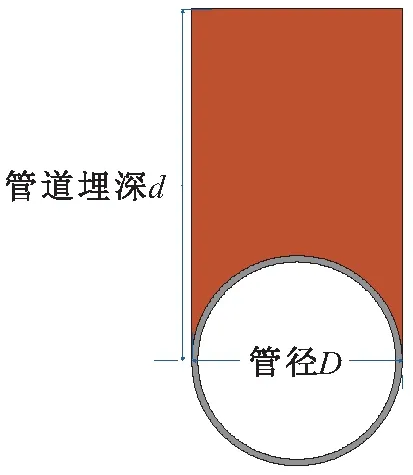
图7 未裸露的埋地管道悬空段受力截面示意图Fig.7 Schematic diagram of stressed section of suspended section of the non-exposed buried pipeline

将土体的重量Q加到有限元分析模型中，得到的有限元模拟结果如下：

(1) 假设管道埋深为1 m:设置管道的悬空长度分别为30 m、40 m、50 m，利用Abaqus有限元分析软件模拟得到不同悬空长度下未裸露的埋地管道应力和应变云图。

将多组数值模拟所得数据进行拟合，得到未裸露的埋地管道最大Mises应力与悬空长度的关系图，见图8。

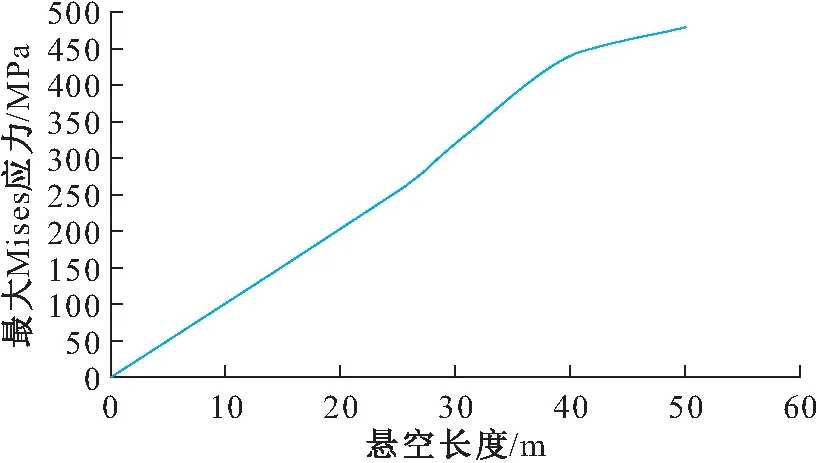
图8 未裸露的埋地管道最大Mises应力与悬空长度的 关系图Fig.8 Relationship between maximum Mises stress and suspension length of the non-exposed buried pipeline

当未裸露的埋地管道的悬空长度为30 m时，管-土接触端上表面的等效应力极大值开始超过管道材料的最大许用应力324 MPa，即管道此时的悬空长度为允许使用的最大安全悬空长度；当未裸露的埋地管道的悬空长度为42 m时，管-土接触端上表面的等效应力极大值开始超过管道材料的屈服强度450 MPa，即管道此时的悬空长度为允许使用的极限悬空长度；之后管材开始进入塑性变形时期，管道上的应力随悬空长度的变化开始变得缓慢。因此，基于应力的失效判据，当管道埋深为1 m时，未裸露的埋地管道的极限悬空长度为42 m左右。

将多组数值模拟所得数据进行拟合，得到未裸露的埋地管道最大应变与悬空长度的关系图，见图9。

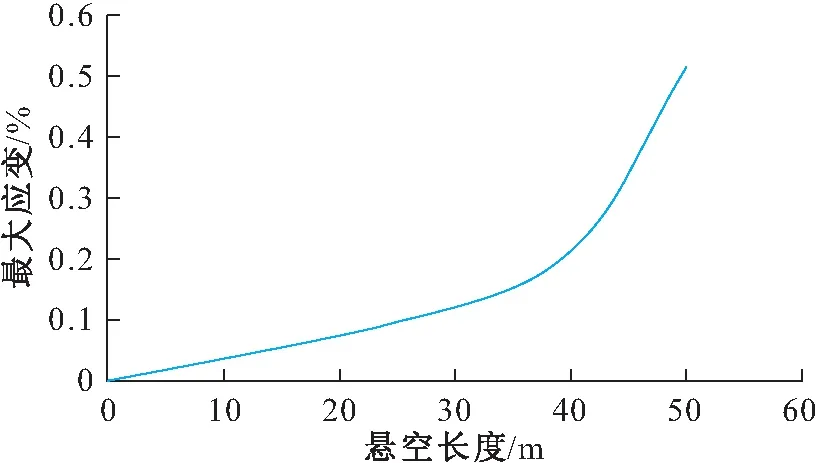
图9 未裸露的埋地管道最大应变与悬空长度的关系图Fig.9 Relationship between maximum strain and suspension length of the non-exposed buried pipeline

当未裸露的埋地管道所受的应力低于管道屈服强度时，管道最大应变随悬空长度的增加缓慢增大；而当未裸露的埋地管道所受的应力超过管道屈服强度时，管道最大应变随悬空长度的增加而急剧增大。当未裸露的埋地管道悬空长度为44 m时，管道达到其最大安全悬空长度；当未裸露的埋地管道悬空长度为50 m时，管道达到其极限悬空长度。因此，基于应变的失效准则，当管道埋深为1 m时，未裸露的埋地管道的极限悬空长度为50 m左右。

(2) 假设管道埋深为1.5 m：设置管道的悬空长度分别为20 m、30 m、40 m，利用Abaqus有限元分析软件模拟得到不同悬空长度下未裸露的埋地管道应力和应变云图。

将多组数值模拟所得数据进行拟合，得到未裸露的埋地管道最大Mises应力与悬空长度的关系图，见图10。

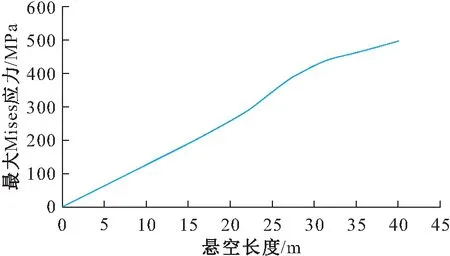
图10 未裸露的埋地管道最大Mises应力与悬空长度的 关系图Fig.10 Relationship between maximum Mises stress and suspension length of the exposed buried pipeline

同上分析，当未裸露的埋地管道的悬空长度为24 m时，管道此时的悬空长度为允许使用的最大安全悬空长度;当未裸露的埋地管道的悬空长度为33 m时，管道此时的悬空长度为允许使用的极限悬空长度。因此，基于应力的失效判据，当管道埋深为1.5 m时，未裸露的埋地管道的极限悬空长度为33 m左右。

将多组数值模拟所得数据进行拟合，得到未裸露的埋地管道最大应变与悬空长度的关系图，见图11。

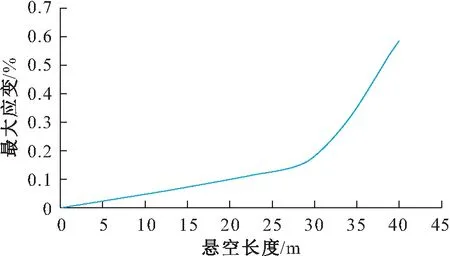
图11 未裸露的埋地管道最大应变与悬空长度的关系图Fig.11 Relationship between maximum strain and suspension length of the non-exposed buried pipeline

当未裸露的埋地管道的悬空长度为34 m时，管道达到其最大安全悬空长度；当未裸露的埋地管道的悬空长度为39 m时，管道达到其极限悬空长度。因此,基于应变的失效准则，当管道埋深为1.5 m时，未裸露的埋地管道的极限悬空长度为39 m左右。

(3) 假设管道埋深为2 m：设置管道的悬空长度分别为25 m、30 m、40 m，利用Abaqus有限元分析软件模拟得到不同悬空长度下未裸露的埋地管道应力和应变云图。

将多组数值模拟所得数据进行拟合，得到未裸露的埋地管道最大Mises应力与悬空长度的关系图，见图12。

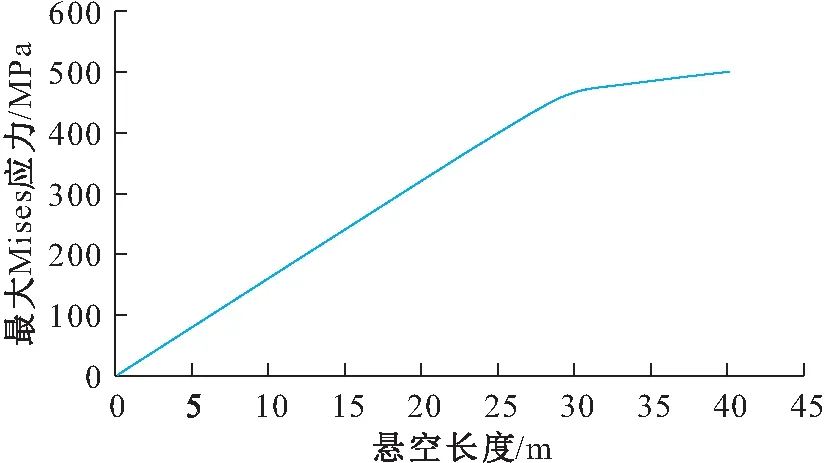
图12 未裸露的埋地管道最大Mises应力与悬空 长度的关系图Fig.12 Relationship between maximum Mises stress and suspension length of the non-exposed buried pipeline

当未裸露的埋地管道的悬空长度为20 m时，管道此时的悬空长度为允许使用的最大安全悬空长度；当未裸露的埋地管道的悬空长度为28 m时，管道此时的悬空长度为允许使用的极限悬空长度。因此，基于应力的失效判据，当管道埋深为2 m时，未裸露的埋地管道的极限悬空长度为28 m左右。

将多组数值模拟所得数据进行拟合，得到未裸露的埋地管道最大应变与悬空长度的关系图，见图13。

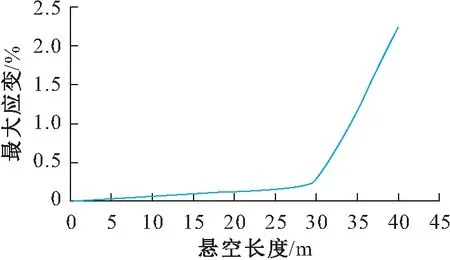
图13 未裸露的埋地管道最大应变与悬空长度的 关系图Fig.13 Relationship between maximum strain and suspension length of the non-exposed buried pipeline

当未裸露的埋地管道的悬空长度为30 m时，管道达到其最大安全悬空长度；当未裸露的埋地管道的悬空长度为32 m时，管道达到其极限悬空长度。因此，基于应变的失效准则，当管道埋深为2 m时，未裸露的埋地管道的极限悬空长度为32 m左右。

3 含腐蚀缺陷的埋地管道悬空段可靠性分析

3.1 基于应力失效判据的管道失效极限状态方程的建立

研究含腐蚀缺陷的埋地悬空管道结构可靠性，首先要对埋地管道悬空段进行受力分析，得到其失效功能函数。假设腐蚀坑缺陷正好位于埋地悬空管道管-土接触位置(管端位置)，由前述可知此时管道的悬空长度极限值最小，可用作建立管道失效的极限状态方程。含腐蚀缺陷的埋地管道管端截面示意图，见图14。

图14 含腐蚀缺陷的埋地管道管端截面示意图Fig.14 Schematic diagram of pipe end of the buried pipeline with corrosion defect

根据von Mises屈服失效准则，基于应力失效判据的含腐蚀缺陷的埋地悬空管道失效功能函数的表达式如下：

(2)

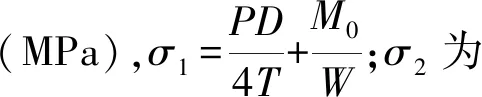
如该模型所示，当埋地管道悬空时，管端上部所受的拉应力最大，由于管道存在腐蚀坑缺陷，因此可以将管道壁厚视为减薄管道壁厚，即：

T=t-Δt

(3)

式中:T为减薄管道壁厚(mm);t为实际管道壁厚(mm)；Δt为管道腐蚀深度(mm)。

当G(X)>0时，表示管道未达到屈服应力，能够正常运行，处于可靠状态;当G(X)<0时，表示管道已进入屈服状态，不能正常工作，处于失效状态;当G(X)=0时，表示管道处于极限临界状态。根据可靠性理论，求解含腐蚀缺陷的埋地管道悬空段可靠度，就是求解G(X)>0的概率。

3. 2 管道随机变量参数的确定

由埋地悬空管道失效功能函数可知，含腐蚀缺陷的埋地管道悬空段的可靠度主要与管道外径D、实际管道壁厚t、管道内压P、管道腐蚀深度Δt、管道屈服应力σs、管道悬空长度L等因素有关，这些变量都具有随机性，且各个随机变量间均具有相关性，会影响到管道可靠度计算的准确性。因此，在本文研究中假设各随机变量相互独立。

通过收集整理文献[8]可知，管道外径D、管道壁厚t、管道内压P、管道腐蚀深度Δt、管道屈服应力σs均为正态分布。由于管道的悬空长度受地质条件及自然环境等因素的影响，其分布类型的确定相对较难，因此为了便于比较，在本文研究中假设管道出现大跨度悬空时，其悬空长度为正态分布。

3. 3 算例分析

本文以西气东输忠武线常用材料X65管线钢作为研究对象，该管道外径D均值为610 mm，实际管道壁厚t均值为8 mm，管道内压P均值为4.3 MPa，管道屈服应力σs均值为450 MPa，管道腐蚀深度Δt均值为3.16 mm，根据基于应力失效判据的管道最大安全悬空长度为83 m，因此选择管道的悬空长度83 m作为均值。通过查阅相关文献，得到X65管线钢材料各随机变量的分布参数，见表5。

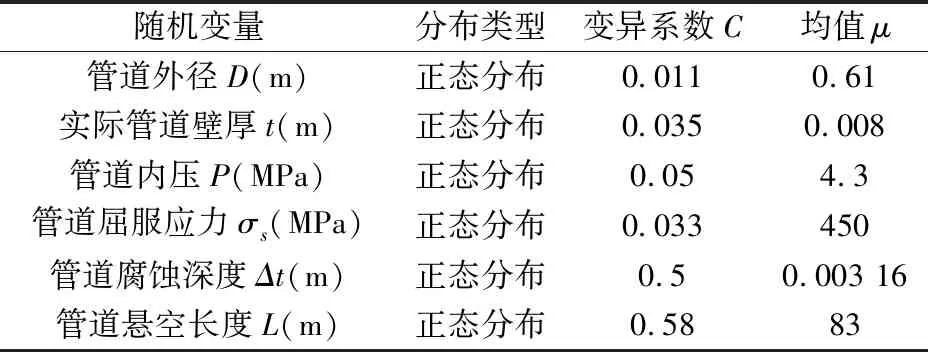
表5 X65管线钢材料各随机变量的分布参数表

随机变量的标准差与均值的关系式如下：

式中：C为变异系数；σ为标准差；μ为均值。

根据算例参数，本文采用蒙特卡洛法对含腐蚀缺陷的埋地管道悬空段的可靠度进行计算，利用Matlab软件进行了105次随机抽样模拟，模拟计算得到该管道结构可靠度为0.911 0。

3.4 腐蚀深度和悬空长度对管道可靠度的影响程度分析

本文在上述建立的裸露的埋地管道悬空段受力有限元分析模型的基础上，加入腐蚀缺陷的影响，提出减薄管道壁厚的计算模型，针对埋地悬空管道应力最大的管端位置，建立了含腐蚀缺陷的埋地管道悬空段的失效功能函数和管道基于应力失效判据的极限状态方程，并利用蒙特卡洛法对管道结构可靠度进行计算，通过Matlab软件进行随机抽样模拟，最后得出模拟结果。

当管道的悬空长度为83 m，且管道的其他随机变量参数不变时，将随机变量管道的腐蚀深度Δt作为唯一变量，可模拟得到管道结构可靠度与管道腐蚀深度之间的关系图，见图15。

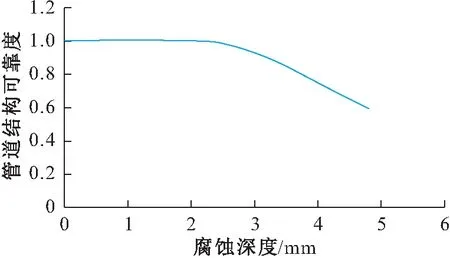
图15 管道结构可靠度与管道腐蚀深度的关系图Fig.15 Relationship between pipeline structure reliability and pipeline corrosion depth

根据ASME B31G标准的规定：当管道腐蚀坑缺陷深度小于0.1倍管道壁厚时可以忽略不计，管道腐蚀坑缺陷深度的最大许可值为0.8倍管道壁厚。

由图15可见，当管道的腐蚀深度小于2.4 mm，即小于0.3倍管道壁厚时，管道结构可靠度基本不受管道腐蚀深度的影响，管道结构可靠度仅从最初的0.998 5下降至0.988 9；而当管道的腐蚀深度大于2.4 mm，即大于0.3倍管道壁厚时，管道结构可靠度开始随管道腐蚀深度的增加而大幅下降，其值从2.4 mm时的0.988 9下降至3.2 mm时的0.904 4，再到4 mm时的0.748。故由此可得出结论：当管道的腐蚀深度大于0.3倍管道壁厚时，管道结构可靠度受管道腐蚀深度的影响严重，此时应及时做好管道抢修与维护工作，以保证管道的安全稳定运行。

当管道的腐蚀深度为2.4 mm且管道的其他随机变量参数保持不变时，将随机变量管道的悬空长度作为唯一变量，可模拟得到管道结构可靠度与管道悬空长度之间的关系，见图16。

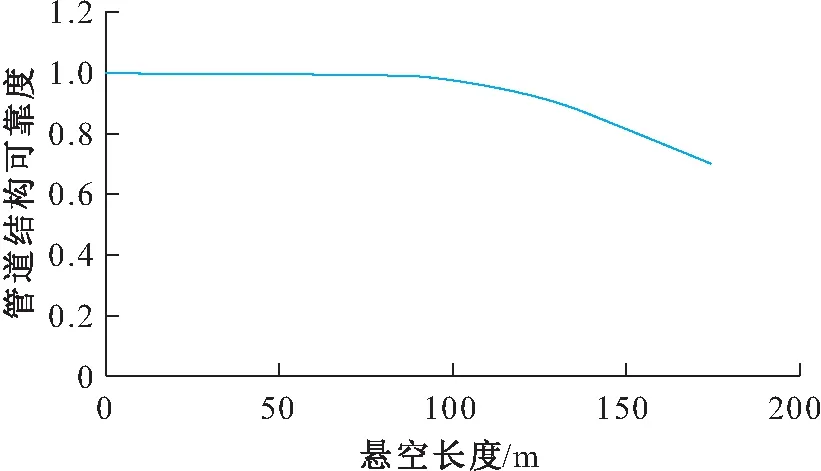
图16 管道结构可靠度与管道悬空长度的关系图Fig.16 Relationship between suspended length of pipelines and reliability of pipeline structure

由图16可见，当管道的悬空长度小于91.3 m时，管道结构可靠度受管道悬空长度的影响较小，管道结构可靠度仅从最初的0.995 6下降至0.985 4；而当管道的悬空长度大于91.3 m后，管道结构可靠度开始随管道悬空长度的增大而大幅下降，其值从91.3 m时的0.985 4下降至174.3 m时的0.700 3。故由此可得出结论：当管道的悬空长度大于91.3 m时，管道结构可靠度受管道悬空长度的影响严重，此时应及时做好管道抢修与维护工作，以保证管道的安全稳定运行。

4 结 论

本文采用Abaqus软件建立了埋地管道悬空段受力分析有限元计算模型，利用该模型分别对裸露和未裸露的埋地管道悬空段受力情况进行了数值模拟，模拟得到埋地悬空管道应力和应变与悬空长度之间的关系，以及不同埋深条件下基于最大Mises应力和最大应变的管道安全悬空长度和极限悬空长度，并得出如下结论：

(1) 埋地悬空管道发生大变形时，管道上最大应力和最大应变出现在管-土接触端上表面，最大垂直位移出现在管道的中端，且它们都随着管道悬空长度的增加而增大。当埋地悬空管道发生弹性形变时，管道最大Mises应力随悬空长度的增加变化较快，管道最大应变随悬空长度的增加变化较慢；而当埋地悬空管道发生塑性变形时，管道最大Mises应力随悬空长度的增加变化较慢，管道最大应变随悬空长度的增加变化较快。

(2) 裸露的埋地管道的悬空长度与管道埋深无关，且基于应力的失效判据相比基于应变的失效判据管道的安全裕度更大；未裸露的埋地管道的悬空长度与管道埋深有关，且管道埋深越大其最大悬空长度越小。

(3) 将结构可靠度理论应用于含腐蚀缺陷的埋地悬空管道安全性评价理论中，采用蒙特卡洛法并利用Matlab软件对含腐蚀缺陷的埋地悬空管道的随机变量进行随机抽样模拟，计算管道结构可靠度，分析管道结构可靠度与管道腐蚀深度和悬空长度的关系，并结合案例对管道安全性进行评价，结果表明：当含腐蚀缺陷的埋地悬空管道腐蚀深度在0.1～0.3倍管道壁厚范围内，且管道的悬空长度不大于91.3 m时，管道结构可靠性和安全性相对较高；当两者有其一超出该范围时，管道结构可靠度开始发生大幅下降，需引起重视，并及时做好补救措施和管道维护工作；当两者皆超出该范围时，管道结构可靠性和安全性受到严重威胁，必须立刻进行管道抢修。

目前我国管道可靠性理论的评价方法还未纳入相关的标准和规范中，只有参考国际上通用的API和DNV等管道目标可靠度标准，因此研究适用于我国各种环境和条件的管道目标可靠度标准已刻不容缓，本文的研究结果可为制定相关的标准和规范提供数据支持。