用于驱动液压缸活塞运动轨迹跟踪的二阶滑模控制

赵春红,张洛平

(1.山西职业技术学院 机械工程系,太原 030006; 2.河南科技大学 机电工程学院,河南 洛阳 471023)

伴随挖掘机的快速发展,其功率也在逐渐增大,挖掘机液压驱动系统也在向着高压方向发展.传统的挖掘机大多采用机械式杠杆手动操作进行液压驱动换向,长时间工作容易产生疲劳.电液阀结合了电子和液压技术各自优点,使挖掘机手动控制进入电液控制阶段[1].挖掘机在执行高精度任务时,若定位不准确,就会造成巨大经济损失.我国对挖掘机电液阀控制研究与国外相比差距还很大,因此,研究挖掘机电液阀驱动控制,对于提高挖掘机整体水平具有重要意义.

为了提高挖掘机电液阀驱动控制精度,很多学者对液压挖掘机控制系统展开研究.文献[2-3]研究了挖掘机变量泵液压模糊PI控制方法,建立阀控非对称液压缸运动位移方程式,设计挖掘机不同动作执行机构的PI控制参数,通过实验验证模糊PI控制特性,从而提高了电控泵响应速度.文献[4-5]研究了挖掘机液压驱动节能控制方法,给出了变量泵节能控制系统结构,根据模糊控制规则,设计了模糊神经网络控制方法,通过仿真验证模糊神经网络控制的有效性,具有很好的节能效果.文献[6-7]研究了挖掘机液压驱动模糊PID控制方法,建立液压多路阀模型,通过Matlab软件验证模糊PID控制效果,缩短上升时间和稳定时间,从而提高了系统输出的稳定性.以往研究的挖掘机液压控制系统在受到环境中的波形干扰时,活塞不能很好地按照预定轨迹运动.对此,本文采用二阶滑模控制系统,采用压力反馈对流量增益进行补偿,借助Matlab软件对跟踪轨迹进行仿真验证,并且与传统PID控制方法进行对比分析,为提高挖掘机电液阀控制精度提供参考价值.

1 液压缸驱动模型

本文采用的液压缸驱动装置如图1所示.

图1 电液阀缸驱动示意图Fig.1 Driving schematic diagram of electro-hydraulic cylinder

活塞位置运动方程式[8]为

(1)

式中:xP为活塞位置;Meq为等效负载质量;PA,PB分别为A腔和B腔压力;AA,AB分别为活塞A侧面积和B侧面积;Bv为粘性阻尼系数;Fad为负载压力;βe为体积模量;VA,VB分别为A腔和B腔的体积;QA,QB分别为A口和B口的流量;CL为泄漏系数;KvA,KvB分别为阀口A和阀口B的流量增益;xv为阀芯位置;ωv为液压固有频率；ξv为压力损失系数；uv阀门输入信号;PS,PT分别为供应压力和油缸压力.

负载压力方程式为

(7)

式中:PL为气缸负载压力；λ为流量增益比；ρ为体积比；μ为面积比.

假设阀泄露流量忽略不计,则可以推导液压空间模型方程式为

(8)

(9)

(10)

(11)

式中：KQ为流量增益.

由于负载和供应压力的变化,导致阀流量增益KQ的变化.因此,采用压力反馈对流量增益进行补偿,其方程式为

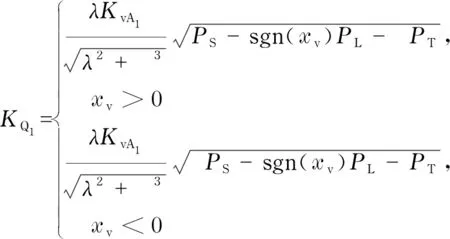
(12)

AAuv1=KQ1uv

(13)

假设KQ≈KQ1,将式(13)代人式(8),可得

(14)

液压驱动通常阻尼较低,采用补偿器进一步降低了阻尼.为了简化,采用压力反馈定律uv1=uc1-kLPL.假设可以忽略非线性摩擦项,并将所讨论的补偿器应用到模型中,可以得到线性化模型传递函数[9]为

(15)

(16)

(17)

ξs=MeqAAkL(μ2+ρ1)βe+Bvρ1VA1·

(18)

式中：uv1为阀口输入信号；uc1为阀口输出信号；XP为活塞输出位移；UC为输出电压；Ks为反馈量；Ts为假设的参数.

从式(17)和式(18)可以发现,压力反馈项可以改善系统的阻尼,而当BvkL项很小时,只会对固有频率产生有限的影响.但是,从式(16)可以看出,压力补偿器降低了系统的增益.引入补偿,并假设系统时间常数足够小,阻尼足够大,则在系统固有频率以下的某个频率范围内,系统可以用给定的积分系统来近似，即

(19)

2 二阶滑模控制器设计

2.1 二阶控制器

控制目标是尽可能跟踪给定参考位置,需要使e=xP-xR=0.利用式(19),闭环系统可以表示为

(20)

(21)

选择合适的参数组成二阶滑模控制器[10]，即

(22)

式中:α,β为控制增益系数.

为了分析该控制器的性能,考虑封闭系统的时间导数为

(23)

式(22)的分析是考虑有限时间收敛特性的,这一结果在稳定性分析中是有用的.

2.2 收敛条件

将闭环控制系统e=(e,e′)=(e1,e2)组成向量的方程式为

(24)

如果每个分量f1,f2是齐次的,则满足以下关系式:

(25)

式中：ε为转速迟缓率.

在特殊情况下κ=-1,控制器为线性的,权重系数设置为r1=δ+1,r2=δ,并且控制器指数表示为

(26)

式中：δ为转速不均匀度.

当e1=e2=0时,控制系统在有限时间内渐近稳定.因此,e1=e2=0是控制系统稳定性收敛的条件.

2.3 稳定性分析

通过对滑模面的考虑,可以得到(e,e′)=(0,0)的稳定性.用恒等式e″=(de′)/(de)e′,求得滑模面内解的梯度,简化后其方程式[11]为

(27)

分离变量进行积分得到

(28)

求解后得到

(29)

对于e″=0,根据式(23)和式(26)可得

(30)

将式(29)代人式(30)变换后,可以得到

(31)

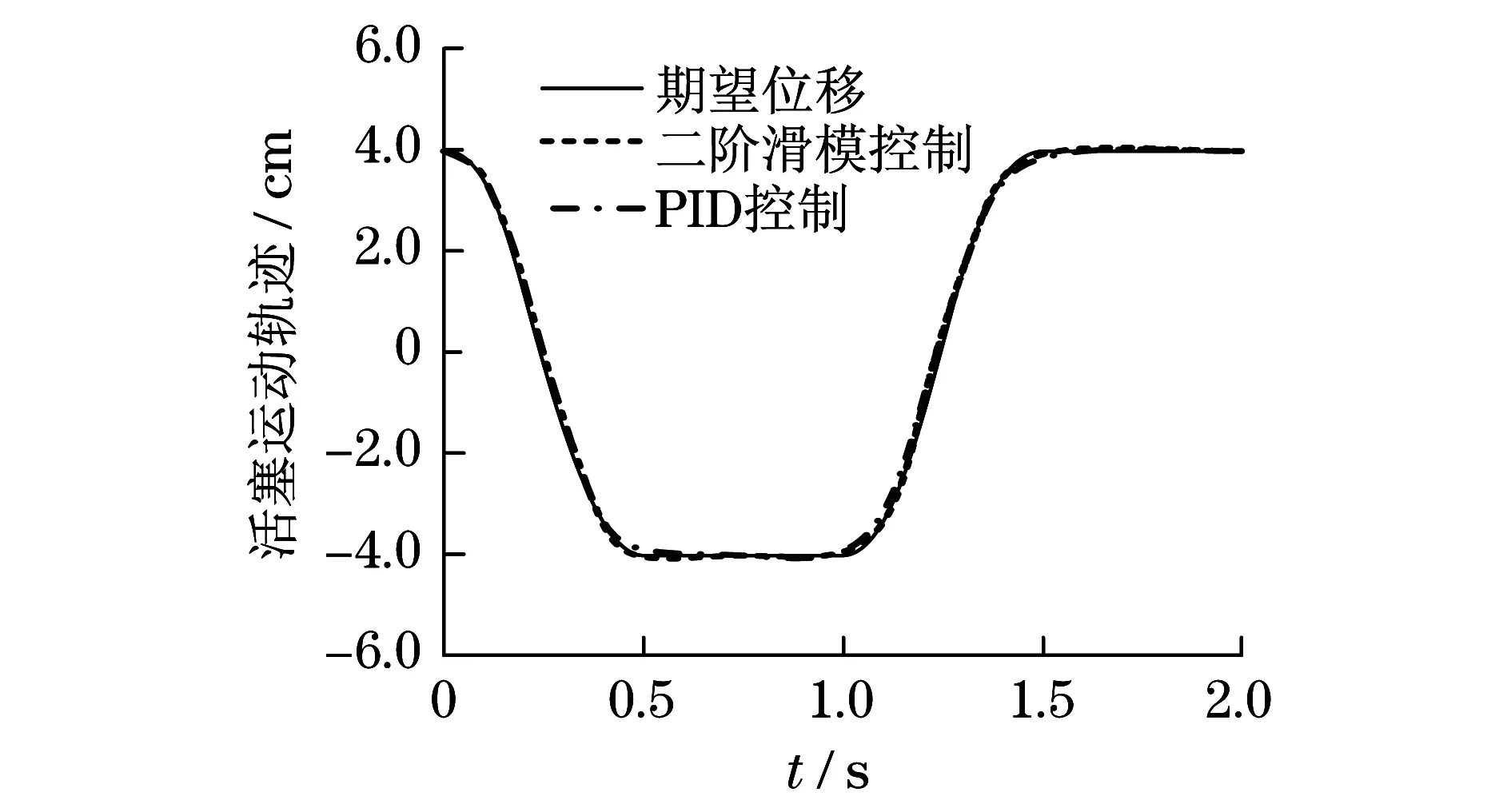
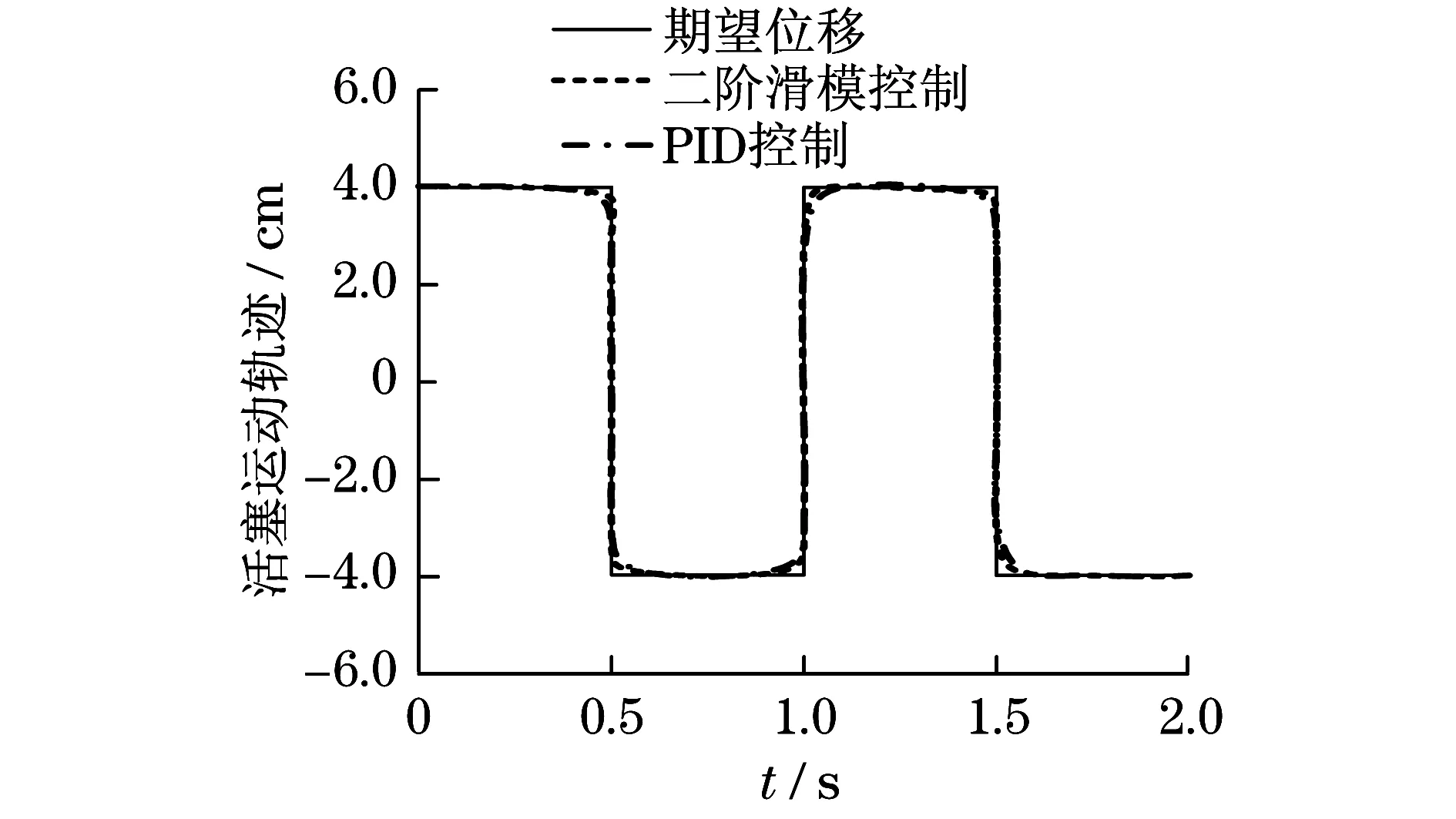
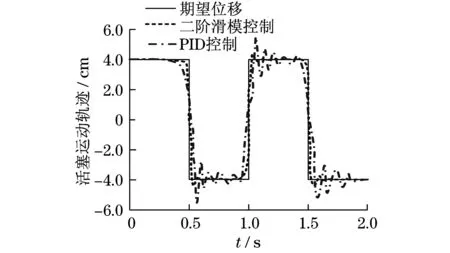
当满足ep2

(32)

因此,二阶滑模控制系统是稳定的.

3 仿真与分析

挖掘机液压缸驱动跟踪轨迹采用二阶滑模控制器,通过Matlab软件对梯形波和方波轨迹跟踪效果进行仿真验证.仿真参数如表1所示.

在无外界波形干扰条件下,对梯形波、方波跟踪效果分别如图2和图3所示.在有外界波形(y=4cos(2πt))干扰条件下,对梯形波、方波跟踪效果分别如图4和图5所示.

图2 梯形波轨迹跟踪(无干扰)Fig.2 Trajectory tracking of trapezoidal waves (no interference)

由图2和图3可知：在无外界波形干扰条件下,采用PID控制和二阶滑模控制液压驱动活塞运动轨迹,跟踪效果较好.由图4和图5可知:在有外界波形干扰条件下,采用PID控制液压驱动活塞运动轨迹,偏离期望位移较大,跟踪误差较大;采用二阶滑模控制液压驱动活塞运动轨迹,偏离期望轨迹较小,跟踪误差较小.因此,二阶滑模控制能够抑制外界环境中的波形干扰,提高活塞运动轨迹跟踪精度,使挖掘机臂定位更加精确.

图3 方波轨迹跟踪(无干扰)Fig.3 Square wave trajectory tracking (no interference)

图4 梯形波轨迹跟踪(有干扰)Fig.4 Trajectory tracking of trapezoidal waves (with interference)

图5 方波轨迹跟踪(有干扰)Fig.5 Square wave trajectory tracking (with interference)

4 结语

本文研究电磁阀缸液压驱动控制,将电磁阀缸用于驱动挖掘机臂,采用二阶滑模控制活塞运动轨迹,主要结论如下:

(1) 二阶滑模控制系统能够根据压力反馈进行在线补偿,具有很好的收敛性,输出更加稳定.

(2) 挖掘机臂液压缸采用二阶模糊控制方法,控制系统反应速度快,其活塞运动轨迹产生误差较小.

(3) 二阶滑模控制方法能够抑制外界波形的干扰,自适应调节负载压力的变化,适合挖掘机高精度定位要求的场合.