摆线钢球行星传动十字槽等速输出机构的力学性能

张 悦 安子军 杨荣刚 姜 威 刘子强

燕山大学机械工程学院，秦皇岛，066004

0 引言

摆线钢球行星传动等速输出机构是一种将行星盘的行星运动转化为定轴转动的机构。十字槽等速输出机构利用钢球作为中介，通过钢球在十字槽中做相对平动，消除偏心距的影响，实现转速的等速输出。十字槽等速输出机构的钢球啮合副在轴向预紧力作用下可以实现无隙等速输出，并能满足不同偏心距的要求，因此成为一种应用广泛的精密等速输出机构[1-2]。

文献[3-6]对摆线钢球行星传动进行了较为深入的理论研究，并设计出一种新型等速输出机构。文献[7]对精密钢球传动环槽等速机构进行了力学性能分析。环槽等速机构的偏心距必须与变速传动部分的偏心距保持严格的一致，这对机构的加工精度与安装精度要求较高，故其应用性受到限制[8]。十字槽等速输出机构能随机适应偏心距，具有良好的实用性[9]。文献[10]根据啮合点法向变形量和法向力的关系，推导出法向力的计算公式，但忽略了摆线槽曲率的影响，所得力学模型不精确。传统十字槽等速机构的槽截面为锥形或球形，当十字槽截面形状为锥形时，啮合刚度较小，易产生较大的弹性回差；当十字槽截面形状为球形时，接触角不容易控制，且随着载荷的变化而发生变化，传动效率和承载能力不稳定，影响机构的传动平稳性。同时，在间隙调解机构轴向预紧力的作用下，啮合副处于四点啮合状态，因此建立四点接触力学模型更加符合实际情况。

1 结构与传动原理

摆线钢球行星传动的结构如图1a所示。等速啮合副为等曲率半径双圆弧十字槽结构，能四点接触，实现无隙啮合。图1b中，β2为啮合点法线与盘平面的夹角，rq为等速钢球半径，rh为十字槽截面曲率半径，且rh=r*rq，其中，r*为半径系数。

1.中心盘 2.减速钢球 3.行星盘 4.输入轴 5.输出轴(盘) 6.间隙调解机构 7.等速钢球2 8.等速钢球1 9.浮动盘(a)传动结构图

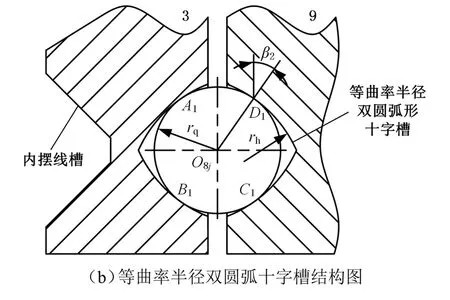
图1 摆线钢球行星传动结构图Fig.1 Structure of cycloid ballplanetary transmission

中心盘右侧加工有齿数为Z1的外摆线槽，行星盘左侧加工有齿数为Z3的内摆线槽，内外摆线槽轴向重合位置处放置Z2个减速钢球。浮动盘左侧加工有一组相互平行、截面为等曲率半径双圆弧形的槽(新型槽)，浮动盘右侧同样加工有一组新型槽，且两组平行槽相互垂直[9]。行星盘右侧加工有与浮动盘左侧同样相互平行的新型槽，输出盘(轴)左侧加工有与浮动盘右侧同样相互平行的新型槽。在行星盘与浮动盘之间的槽中放置Z8个等速钢球，在浮动盘与输出盘之间的槽中放置Z7个等速钢球。机构运转时，输入轴偏心段带动行星盘转动，行星盘推动减速钢球运动，减速钢球在中心盘的限制作用下反推行星盘，使行星盘以较低的转速转动，从而实现减速。行星盘通过等速钢球1、等速钢球2以及浮动盘将转速等速传递给输出盘(轴)，从而实现转速的等速输出。十字槽等速输出机构的等效机构为十字滑块机构。

2 法向力计算

2.1 未承受工作载荷时

受力分析如图2所示。XO1Y为固定坐标系，X3O3Y3为与行星盘固连的随动坐标系[11]，X9O9Y9为与浮动盘固连的随动坐标系，O1、O3、O8、O9分别为中心盘几何中心、行星盘几何中心、等速钢球组1分布圆中心以及浮动盘几何中心在XO1Y平面上的投影，O8j为等速钢球组1第j个钢球球心。α8为等速钢球组1中相邻钢球球心与其分布圆中心的夹角，Φ3为行星盘绕其几何中心转过的角度。Rw为等速钢球组分布圆半径，输入轴偏心距为2e(点O1和O3之间的距离)。

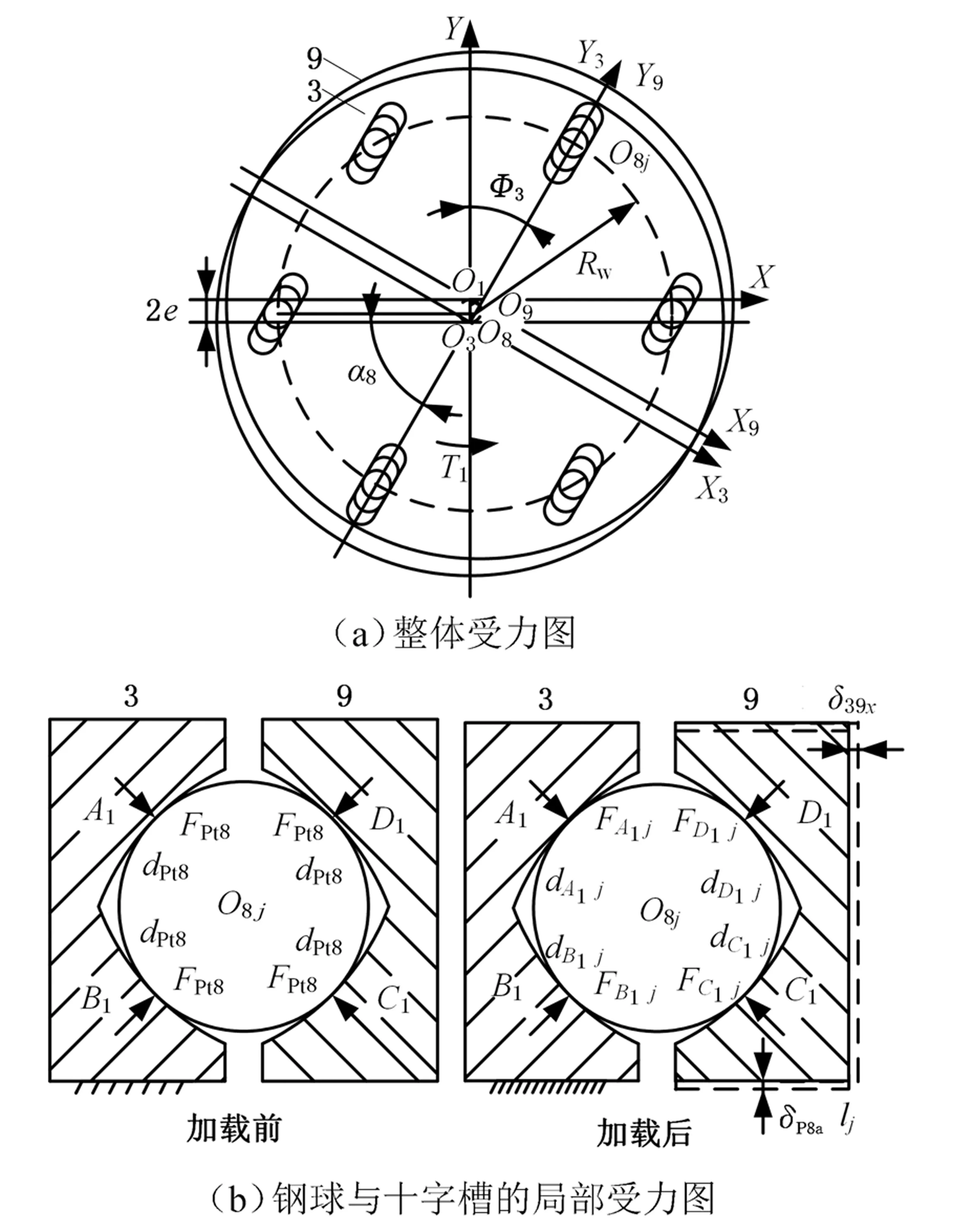
图2 等速啮合副受力图Fig.2 The force diagram of equi-speed engagement pair

如图2b所示，在轴向预紧力Ft的作用下，各个钢球处于四点啮合状态，浮动盘相对行星盘的轴向微位移为δ39x。由文献[12]可知，啮合点处啮合刚度为啮合位置的函数，而本文中十字槽截面为等曲率半径的双圆弧形，故Z8个钢球平均承担Ft，每个钢球承担的轴向预紧力为Ft8。各个啮合点处的法向预紧力均为FPt8，各个啮合点处的预变形量为δP8a，则有

(1)

由几何关系可得浮动盘相对于行星盘的轴向微位移：

δ39x=2δPt8/sinβ2

(2)

根据赫兹接触理论可知，在接触区域内，两弹性体因弹性变形而引起的弹性趋近量[13]为

式中，F为作用于接触点的法向力；K*、a*为Hertz接触系数；E1、E2为两弹性接触体的弹性模量；μ1、μ2为两弹性接触体的泊松比；∑ρ为接触点处4个主曲率之和。

联立式(1)～式(3)可得轴向微位移：

(4)

2.2 承受工作载荷时

如图2b所示，行星盘顺时针转动时，浮动盘受到阻力矩T1的作用，浮动盘实际转角产生滞后量α39以及浮动盘相对行星盘轴向微位移变化量Δδ39x，则传力侧与非传力侧的变形协调方程为

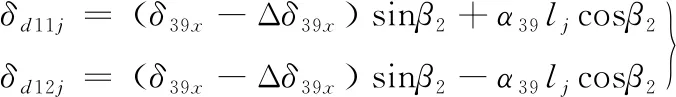
(5)

j=j1，j2

式中，lj1为位于坐标轴X9上方第j1个钢球的力臂；lj2为位于坐标轴X9下方第j2个钢球的力臂；[Z8/4]为对Z8/4取整。

在阻力矩和预紧力共同作用下，啮合点A1、B1、C1、D1的法向力分别为FA1j、FB1j、FC1j、FD1j，法向力满足下列关系

(6)

由Hertz点接触理论可知，啮合法向力与法向变形量的非线性关系为[13]

(7)

式中，δi为啮合点处的法向变形量。

联立式(3)、式(5)～式(7)可得传力侧与非传力侧的法向力：

(8)

式中，GA1、GB1、GC1和GD1分别为啮合点A1、B1、C1、D1处的变形系数。

对浮动盘建立轴向力和力矩平衡方程：

(9)

本文以位于X9轴上方且位于Y9轴上的十字槽为例，分析传力侧法向力FC1和非传力侧法向力FD1的变化规律。如图3所示，转角3从0变化至2π时，钢球在浮动盘上十字槽的位置如下：低端中点顶端中点低端，即法向力FC1和FD1完成了一个周期的变化。

图3 法向力FC1和FD1随转角φ3变化曲线Fig.3 Curves of normal force FC1 and FD1 with angle φ3

3 接触应力分析

3.1 接触应力计算

如图4所示，由赫兹接触理论可知，两弹性体在点Oi处接触，在载荷F的作用下，接触点扩展为椭圆接触区，接触区域长短半轴的长度分别为a、b，中心点的接触应力为q0，中心点的变形量为d0。

图4 接触模型图Fig.4 Diagram of contact model

根据Boussinesq关于弹性半空间体在集中力作用下的应力结果[14]可知，在法向力F的作用下，采用文献 [15]的方法，可以推导出接触表面下不同深度处主应力σx、σy和σz在直角坐标系下的计算公式：

(10)

(11)

(12)

式中，k为接触椭圆长短半轴比值的倒数；e0为接触椭圆偏心率，e0=(1-k2)1/2；M(φ,e0)为第一类不完全椭圆积分；L(φ,e0)为第二类不完全椭圆积分；ξ为量纲一深度，ξ=z/a；φ为辅助角，φ=arccotξ。

联立式(10)～式(12)，可得接触表面下的切应力

τ=(σz-σy)/2

(13)

3.2 接触参数求解

根据文献[16]的分析，可采用由文献[17]提出的Hertz接触的迭代算法对接触参数进行精确求解。

令

(14)

则可得参数λ：

(15)

文献[17]提出了一种利用标准完全椭圆积分化简式(15)的简便方法：

(16)

将式(16)对m进行求导，得

(17)

式(16)可用Newton迭代法进行求解，假设m′i是m′(m′=k2)的一个近似值，则比m′i更好的m′的近似值为

完全椭圆积分K(m)、E(m)采用迭代法进行求解,在求解K(m)、E(m)时考虑到迭代的收敛速度，初始值取m=λ2。则椭圆接触区域长短半轴长度a、b分别为

在接触椭圆区域中，最大的接触压力位于接触区域的中心处，其值为平均压力的3/2倍，即

(18)

接触椭圆区域中心点的法向变形量为

4 参数影响分析

4.1 参数对法向力的影响分析

样机参数取值见表1(下文未注明时取该组参数)。

表1 计算参数

本文主要讨论参数e、钢球分布圆半径Rw、钢球数Z8、阻力矩T1和轴向预紧力Ft分别对传力侧和非传力侧法向力的影响(本文取Φ3=0)。由图5～图9可得：

(1)随e的增大，传力侧法向力FC1减小，非传力侧法向力FD1增大。当e从1.4 mm增至1.8 mm时，法向力FC1和FD1分别变化了0.019 N和0.017 N，可以忽略e对FC1和FD1的影响。

(2)随分布圆半径Rw的增大，传力侧法向力FC1减小，非传力侧法向力FD1增大。增大Rw可以提高机构承载能力，但会增大传动机构的体积。

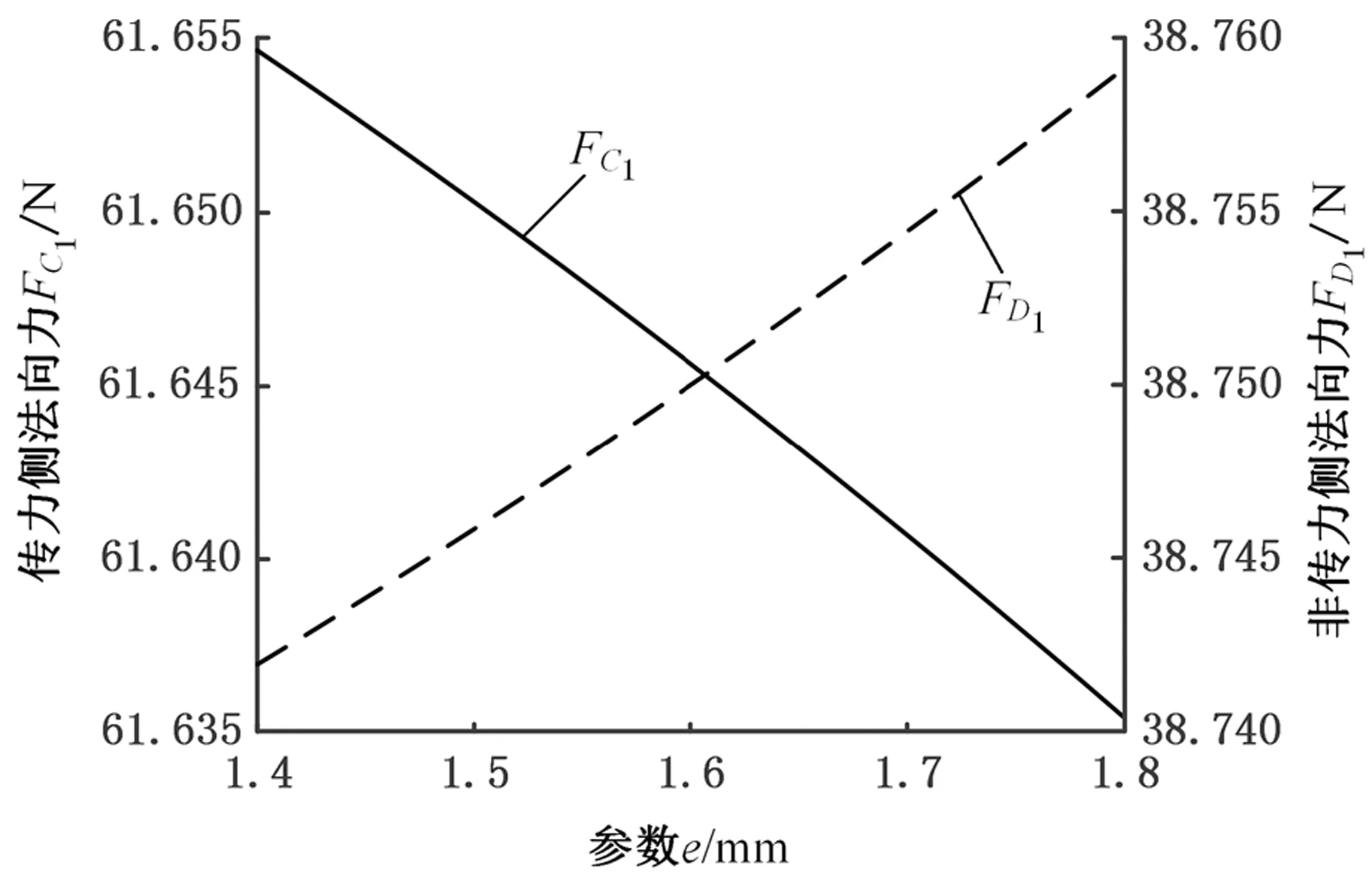
图5 法向力随参数e变化曲线Fig.5 The curves of normal force with e

图6 法向力随半径Rw变化曲线Fig.6 The curves of normal force with radius Rw

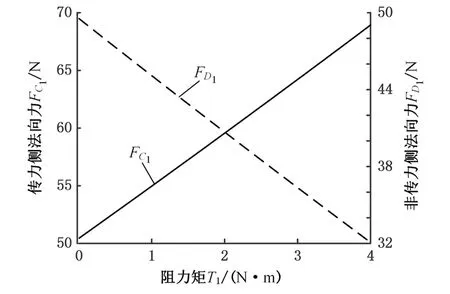
图7 法向力随阻力矩T1变化曲线Fig.7 The curves of normal force with resistance torque T1

图8 法向力随轴向预紧力Fa变化曲线Fig.8 The curves of normal force with axial preload Fa

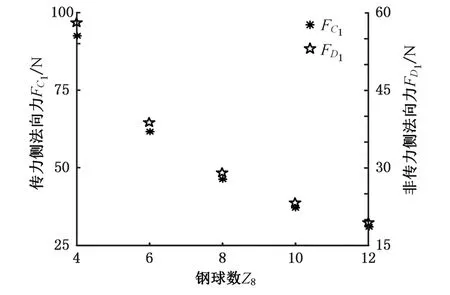
图9 法向力随钢球数Z8变化曲线Fig.9 The curves of normal force with steel ball number Z8

(3)随阻力矩T1的增大，转角滞后量增加，使得传力侧变形增大，非传力侧变性减小，进而使得法向力FC1增大，法向力FD1减小。

(4)随轴向预紧力Ft的增大，传力侧和非传力侧的变形量均增大，进而使得法向力FC1和FD1均增大。Ft<60N时，阻力矩产生的转角滞后量较大，抵消非传力侧的预变形量，使得式(5)中的δd12j<0，由式(8)可得FD1=0。此时，非传力侧因存在间隙而产生回差，影响十字槽等速输出机构的传动精密性。

(5)由于十字槽呈对称分布，且本文中每个十字槽放置1个钢球(实际上可以放置多个钢球)，故钢球数Z8取偶数。随钢球数Z8的增大，传力侧法向力FC1和非传力侧FD1均减小。在其他参数不变的情况下，增加钢球既可以提高十字等速输出机构的承载能力，又不会影响机构的体积。

(6)钢球数Z8对法向力的影响最大，输入轴偏心距对法向力的影响最小，并且可以忽略不计。

4.2 参数对正应力的影响分析

如图10所示，在其他参数不变的情况下，σx、σy和σz均随钢球半径rq的增大而减小，且曲线斜率的绝对值减小。为避免在接触表面应力达到极限，且不发生屈服现象，钢球半径rq尽量取大值。

图10 接触区应力随钢球半径rq变化曲线Fig.10 Curves of contact stress with steel ball radius rq

如图11所示，在其他参数不变的情况下，σx、σy和σz均随r*的增大而增大，且曲线斜率减小。为避免在接触表面应力达到极限，且不发生屈服现象，半径系数r*取小值。

如图12所示，在其他参数不变的情况下，正应力σz随x的增大而减小，且曲线斜率的绝对值先增大后减小；σx、σy均随x的增大而减小，且曲线斜率的绝对值减小。正应力σy逐渐趋于0，在ξ=1时，σy=0。

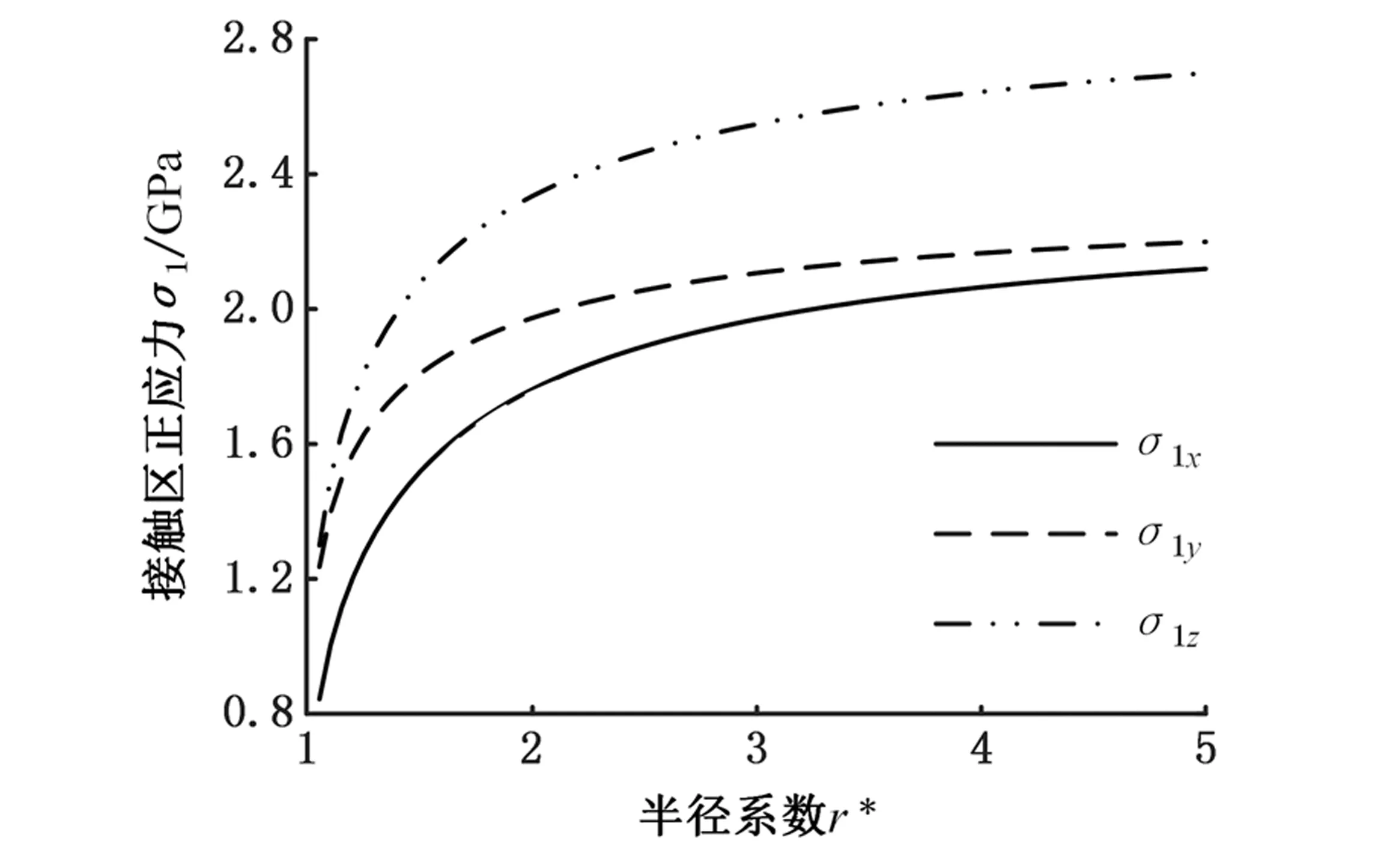
图11 接触区应力随半径系数r*变化曲线Fig.11 Curves of contact stress with radius coefficient r*

图12 接触区应力随量纲一深度ξ变化曲线Fig.12 The curves of contact stress with dimensionless depth ξ

4.3 参数对切应力的影响分析

如图13所示，在其他参数不变的情况下，切应力τ随rq的增大而减小，且曲线斜率的绝对值减小。当rq从1.5 mm增至4 mm时，能够满足大多数材料许用切应力的要求。

图13 切应力随钢球半径rq变化曲线Fig.13 Curves of shear stress with steel ball radius rq

如图14所示，在其他参数不变的情况下，切应力τ随r*的增大而增大，且曲线斜率减小。当r*从1.05增至5时，能够满足大多数材料许用切应力的要求。

如图15所示，在其他参数不变的情况下，随ξ的增大，切应力τ先增大再减小。在量纲一深度ξ=0.367时，τ达到最大值，τmax=750.40 MPa。

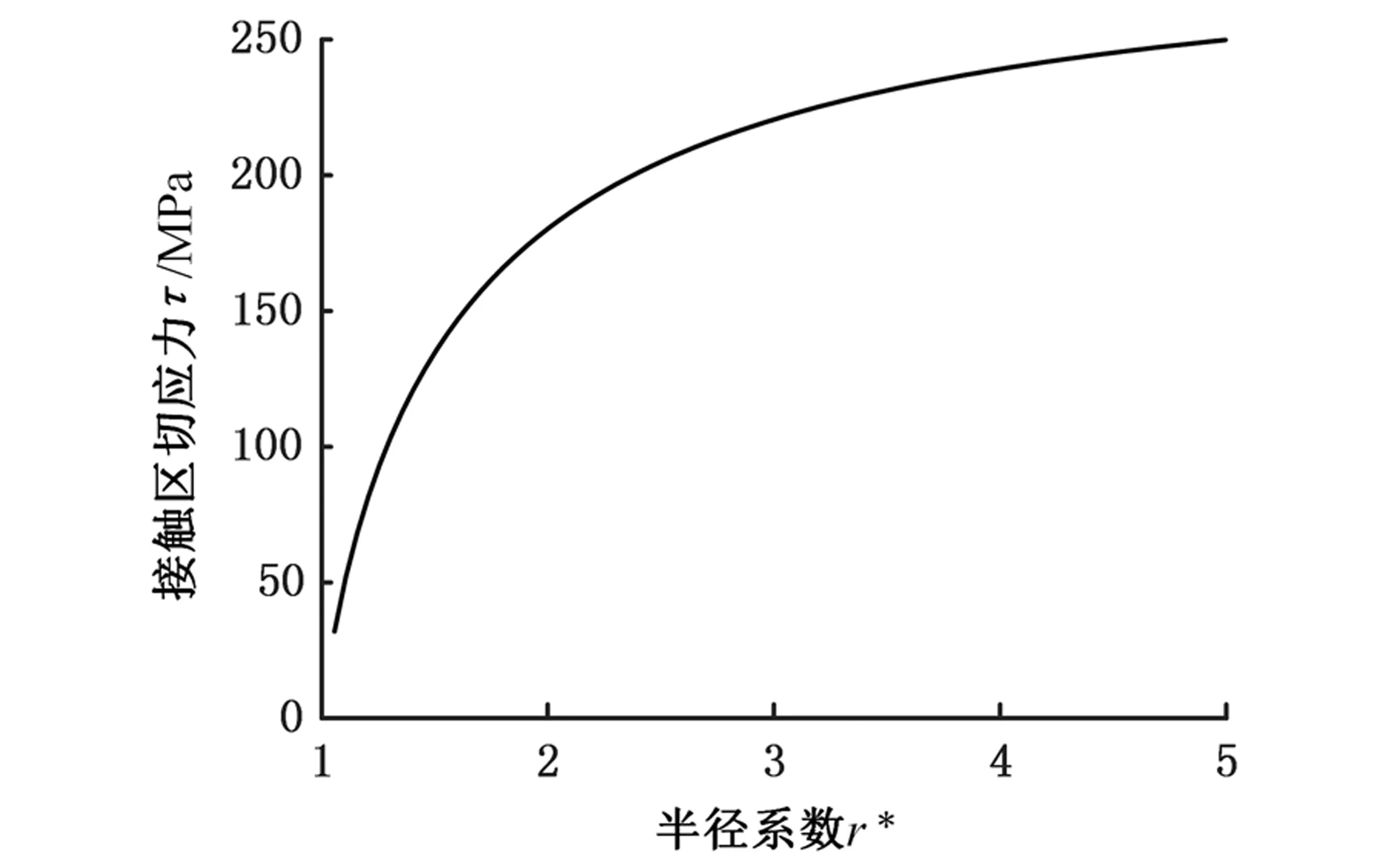
图14 切应力随半径系数r*变化曲线Fig.14 Curves of shear stress with radius coefficient r*

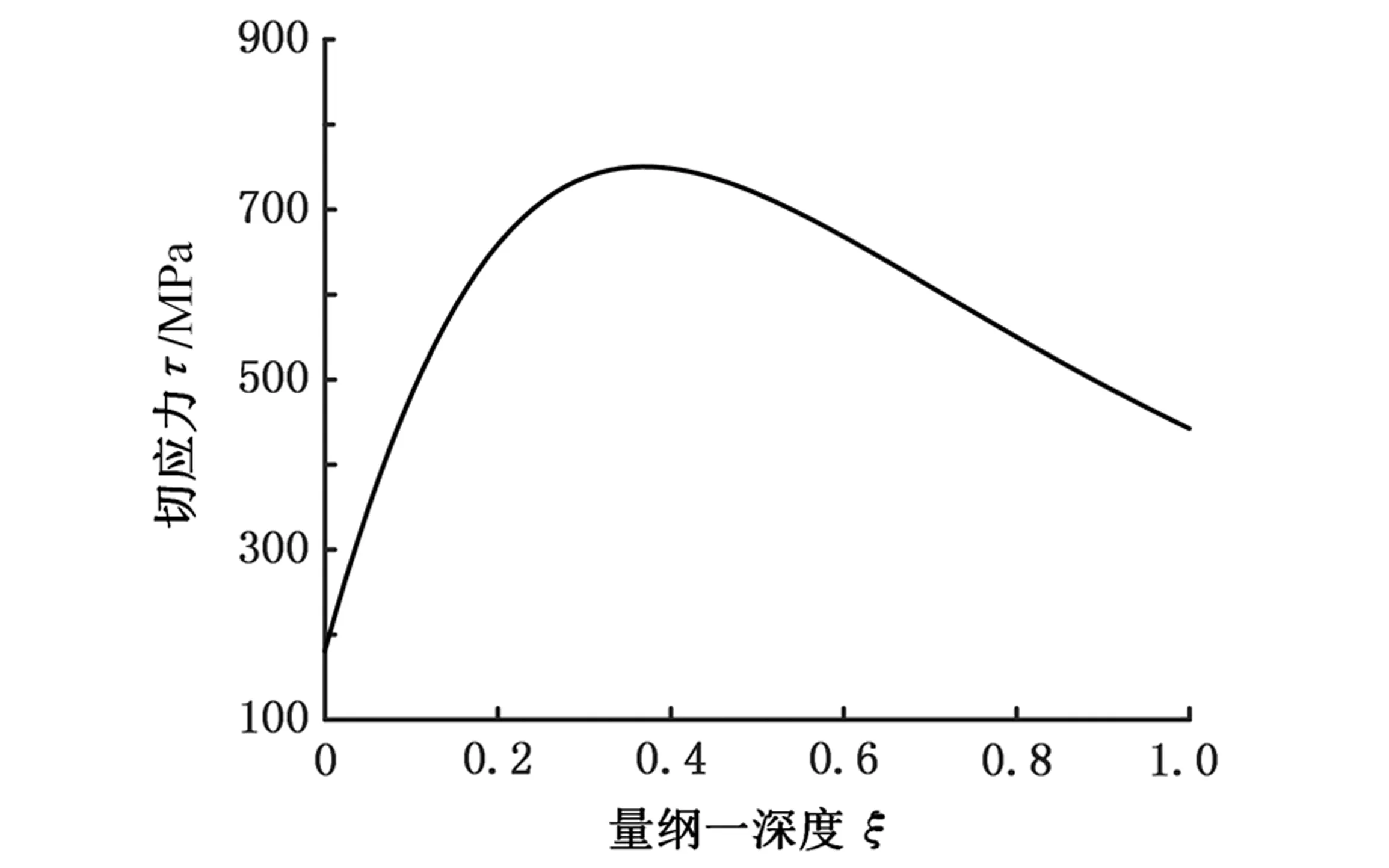
图15 切应力随量纲-深度ξ变化曲线Fig.15 Curves of shear stress with dimensionless depth ξ

如图16所示，随钢球半径rq的增大，切应力峰值τmax逐渐减小，且曲线斜率的绝对值减小。rq从1.5 mm增至4 mm时，峰值τmax减小了506.31 MPa。切应力峰值对应的深度为定值，即ξ与钢球半径rq无关。为避免在切应力的作用下，材料沿轴线45°方向产生滑移面以及接触表面产生点蚀，rq取大值。

图16 切应力峰值和量纲一深度随钢球半径rq变化曲线Fig.16 Curves of shear stress peak and dimensionless depth with steel ball radius rq

如图17所示，随半径系数r*的增大，切应力峰值τmax逐渐增大，且曲线斜率减小。当r*从1.05增至5时，峰值τmax增大了436.23 MPa。切应力峰值所对应的量纲一深度ξ也随r*的增大而增大。为避免在切应力的作用下，材料沿轴线45°方向产生滑移面以及接触表面产生点蚀，r*取小值。

图17 切应力峰值和量纲一深度随钢球半径r*变化曲线Fig.17 Curves of shear stress peak and dimensionless depth with radius coefficient r*

5 结论

(1)利用啮合点法向变形量与轴向微位移的几何关系，根据赫兹理论以及平衡方程，求得了轴向微位移的精确计算公式。建立啮合副四点力学模型，得到了啮合法向力的精确计算公式。

(2)传力侧和非传力侧的法向力均呈周期性变化。参数e、Rw、Z8、T1和Ft对传力侧和非传力侧的法向力均有影响，其中，钢球数Z8的影响最大，输入偏心轴偏心距的影响最小。轴向预紧力过小时，传动机构的非传力侧会出现间隙，从而产生回差，最终影响机构的传动精密性。

(3)增大钢球半径rq可以减小应力σx、σy、σz、τ以及切应力峰值τmax；减小半径系数r*可以减小应力σx、σy、σz、τ、切应力峰值τmax以及切应力峰值所对应的深度值ξ。