基于低分辨率位置传感器的永磁同步电动机转矩脉动控制

杨定成,许 俊

(1.浙江东方职业技术学院 数字工程学院,浙江 温州 325000; 2.江西理工大学 机电工程学院,南昌 330003)

近年来,车辆节能已成为世界范围内的一个重要问题[1-2],因此,由电动机驱动的电动汽车和混合动力汽车在市场上逐渐兴起,并且一些液压控制的机械系统已被电动机驱动系统取代,比如动力转向和制动系统.电动机助力转向系统(Electronic Performance Support System,EPSS)具有燃油效率高、转向性能好、环境友好性好等优点被逐渐应用于汽车中,此外,与传统液压助力转向相比,元件数量减少使得整体尺寸缩小[3-4].由于永磁同步电动机效率高、寿命长、转动惯量小以及散热性能好等优点[5],故使用它代替永磁直流电动机驱动EPSS,但仍存在一些缺点,例如噪声、机械振动需要一个额外逆变器驱动电路，导致经济成本增加[6].噪声和振动主要由电动机的转矩脉动产生,转矩脉动是由机械不平衡、定子和转子磁芯中的磁饱和以及齿槽转矩等原因综合作用产生的,因此，减小转矩脉动能够降低噪声和振动[7].

减小转矩脉动通常有两种方法:基于电动机结构和电动机控制器.基于电机结构减少转矩脉动是通过偏转转子和改进转子结构来减少齿槽转矩[8-10].基于电动机控制器减少转矩脉动是通过对磁体饱和进行非线性分析，得出用于抵消特定转矩谐波的补偿电流将补偿电流添加到电流命令中，从而减少转矩[11-12].为了将高频补偿电流和正弦电流应用于永磁同步电动机,在EPSS中通常使用由磁轮、霍尔效应传感器和增量式编码器组成的低成本转子位置传感器获得转子位置的精确信息.为了降低材料成本,由低成本霍尔效应传感器代替编码器驱动IC,但是增量式编码器的分辨率会降低到64 PPR.

本文提出了采用低分辨率增量式编码器减小转矩脉动的方法,分析了增量式编码器分辨率对转矩脉动的影响,转子位置由低分辨率编码器信号估算.为减小由机械不平衡、磁饱和以及齿槽转矩引起的转矩脉动,将补偿的q轴电流加到参考电流指令上.实验结果验证了提出的基于估算的转子位置使转矩脉动减小了性能.

1 转矩脉动分析

1.1 永磁同步电动机建模

在EPSS中,当驾驶员操纵方向盘时,方向盘转矩通过转矩传感器测量,传感器所测得的转矩信号被传输到控制电动机转矩的电子控制单元(Electronic Control Unit,ECU)中,ECU产生一个转矩指令输送给电动机,使其产生转向力并产生所需的转矩.平面安装的永磁同步电动机(Surface Permanent Magnet Synchronous Motor,SPMSM)在轴系abc下电压方程可以表示为

(1)

式中:vabc,iabc分别为定子电压与定子电流;eabc为感应定子绕组中的反电动势;rs,Ls分别为相电阻和相电感.

abc框架电压方程可以转化为转子坐标系中的dq轴电压方程,即

(2)

式中:φf为磁通量;ωr为转子的电角速度；vd，vq分别为d轴和q轴电压;Ld，Lq分别为d轴和q轴电感;id，iq分别为d轴和q轴电流.

SPMSM中的相电感几乎是恒定的,因此，可以认为d轴电感和q轴电感相等.电动机的机械动力学取决于产生的转矩、转子惯量、摩擦和负载转矩.

SPMSM的转矩方程可以表示为

(3)

式中:P为极数;J为惯性动量;B为黏滞摩擦系数;Tf,Tc，TL分别为摩擦转矩、齿槽转矩和负载转矩.

1.2 转矩脉动分析

编码器信号通过每转脉冲的数量进行量化,与实际转子位置相比,低分辨率编码器的转子位置具有量化的转子位置误差,该误差会导致相电流失真,并且会在永磁同步电动机中产生转矩脉动.电动机电流通过量化的编码器信号控制,控制器的dq轴可以根据实际的转子位置来超前或滞后实际的dq轴,电流矢量及其对dr-qr轴和de-qe轴的投影如图1所示.

图1 电流矢量投影Fig.1 Current vector projection

图1中:dr-qr轴是基于高分辨率的实际转子位置;de-qe轴可以视为基于编码器转子位置的假想轴;角度差Δθ表示实际转子位置θr与编码器转子位置θenc之间的位置误差I*.

假设电流矢量超前反电动势矢量α角度,则dr-qr框架和de-qe框架中的dq轴电流分别为

式中：I*为dr-qr轴和de-qe轴下的控制器电流矢.

在SPMSM的低速运行区域中,q轴电流控制电动机转矩,d轴电流被控制为零并在最大转矩/安培(Maximum Torque Per Amper,MTPA)模式下运行.在MTPA区域,图1中的α角被设置为零,因此,式(4)和式(5)中的dq电流为

由于编码器信号的分辨率足够高,因此,对于高PPR编码器,实际转子位置与编码器转子位置之间的转子位置差异较小,但对于低PPR编码器转子位置差异变大,降低了转矩和电流控制性能.检测到的编码器转子位置可表示为

(8)

式中:Nenc为每次机械旋转的编码器脉冲数;n为编码器脉冲指数.

图2为实际转子位置和64 PPR(脉冲/转)编码器检测到的转子位置,将实际转子位置与编码器检测到的转子位置之间的位置误差定义为Δθ=θr-θenc,则最大转子位置误差为

(9)

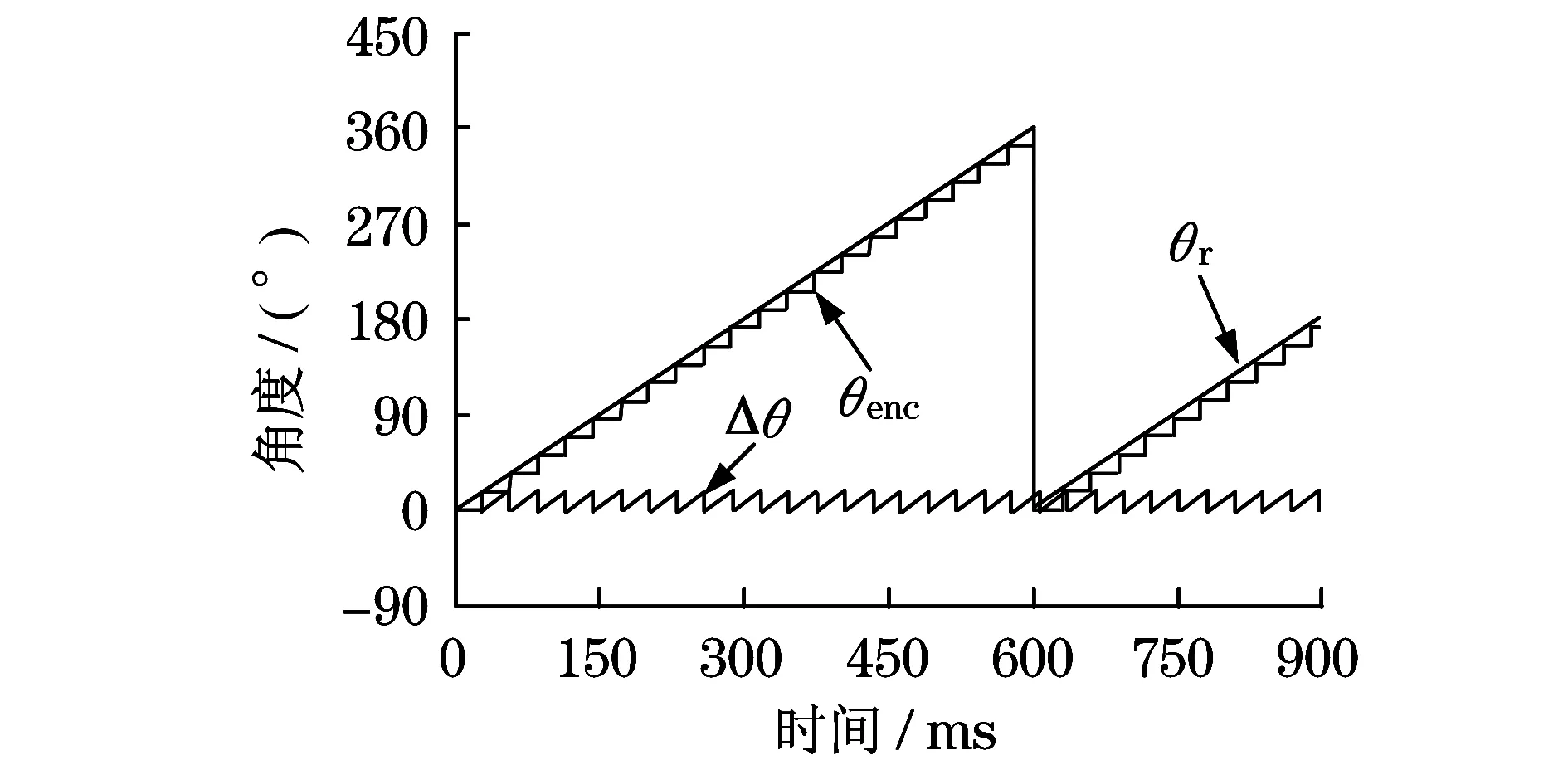
图2 实际的转子位置和量化的编码器转子位置Fig.2 Actual rotor position and quantized encoder rotor position

从式(7)可以看出,当检测到的转子位置相对于实际转子位置具有位置误差Δθ时,由于q轴电流减小而使产生的转矩减小.由式(3)、式(6)、式(7)和式(9)可以推导出实际转子位置控制和编码器信号控制的转矩之间的转矩差为

(10)

由图2可知,式(10)中的位置误差Δθ在编码器脉冲的每个周期出现重复的锯齿波形,使得转矩差具有相似的波形.因此,由式(9)和式(10)可推导出最大转矩差为

(11)

式(11)给出的转矩差是指量化转子位置产生的转矩脉动,因此,编码器信号的转矩脉动性能指数可以定义为

(12)

图3为转矩脉动随6极永磁同步电动机的编码器脉冲数变化曲线,750 PPR以上的转矩脉动低于0.1%,但随着编码器信号数量的减少,300 PPR区域以下的转矩脉动呈指数增长,300 PPR编码器的转矩脉动为0.44%,而在64 PPR时,仅通过编码信号的量化即可增加至4.3%.由于电动机齿槽转矩、摩擦转矩等因素的影响,实际系统中的转矩脉动可能大于分析的转矩脉动.因此,减少编码器信号的量化误差非常重要,特别是对于PPR低的编码器.

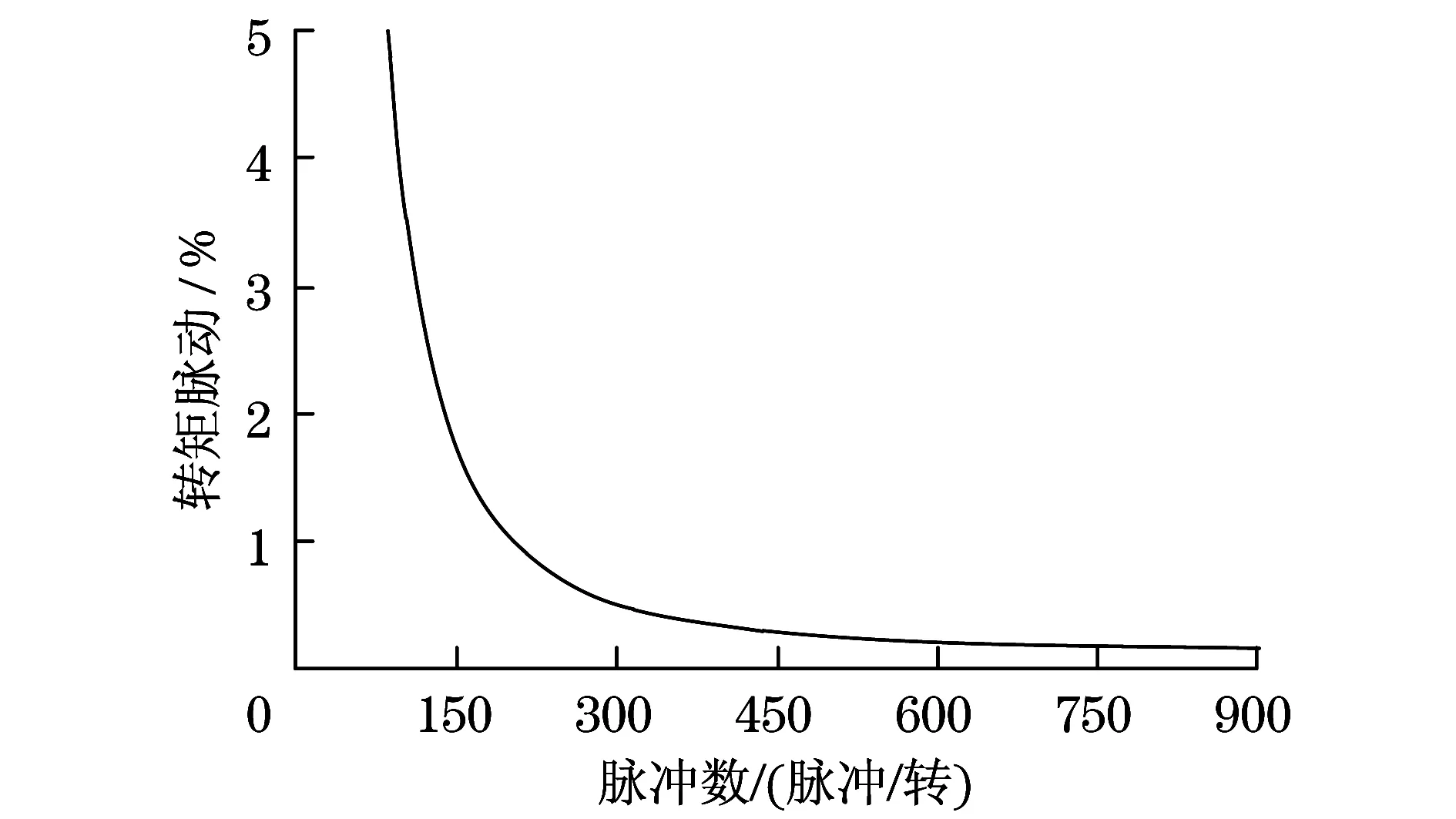
图3 转矩脉动与编码器脉冲数关系Fig.3 Torque ripple is related to the number of encoder pulses

2 转矩脉动减小策略

2.1 转子位置估算

本文使用的SPMSM拥有3相6极,通过霍尔效应传感器的电度角为60°的绝对转子位置与从霍尔效应传感器获得的低分辨率增量编码器位置相结合来检测绝对转子位置.64 PPR的低分辨率编码器的机械角分辨率为5.625°,电度角为16.875°,如此低的PPR位置信息会产生严重的电流谐波和转矩波动.通过对编码器信号的上升沿和下降沿进行适当的信号处理,可获得更精确的转子转速和转子位置.

为了从编码器信号估算转子速度,本文通过测量编码器信号的相邻上升沿周期来估算电动机转速.编码器信号的相邻上升沿之间的周期,可以通过计算高频计数信号的数量来测量.编码器信号、PWM计数信号和转子位置估算的计数器之间的关系,如图4所示.

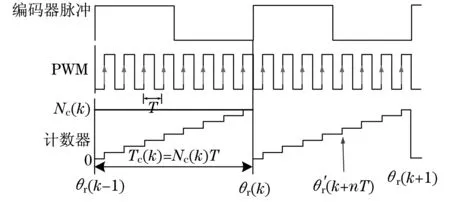
图4 脉冲和转子位置估算Fig.4 Pulse and rotor position estimation

当Nc(k)是编码器信号的第(k-1)次和第k次上升沿之间计算的脉冲数时,编码器脉冲的两个上升沿之间的时间为

(13)

式中:T为PWM计数信号的采样周期.

如果电动机转速为60 r/min,64 PPR编码器信号的频率为64 Hz,则计算的脉冲数Nc(k)为312.脉冲数计数值在较低的速度下会增加,在较高的速度下会减少.

根据编码器信号的两个边沿之间检测到的时间,可以计算出电动机的机械频率为

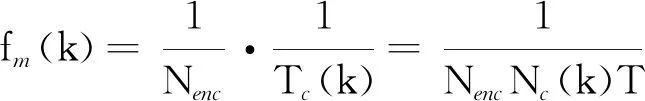
(14)

(15)

(16)

可以注意到,在每个脉宽调制(Pulse Width Modulation,PWM)采样时间皆能够估算编码器信号的上升沿之间的转子位置,且估算的转子位置也在编码器信号的每个上升沿位置进行校准.此外,绝对转子位置每60°电度角更新一次.

2.2 转矩脉动减少策略

电动机转矩脉动主要由数个6阶谐波组成,如图5所示.

图5 转矩脉动和近似值Fig.5 Torque ripple and approximation

从图5中可以看出：转矩脉动波形包含多种谐波,因此，很难对转矩脉动进行精确建模.但可以通过施加额外的电流来抵消6阶转矩谐波,从而降低转矩脉动.图5中的6阶转矩谐波取决于平均转矩和转子位置,它可以近似表示为

(17)

式中:iqo为与平均转矩相对应的标称q轴电流.

根据图5中测得的转矩脉动可以确定6阶转矩谐波系数k6为

(18)

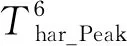
将抵消6阶转矩谐波的额外转矩添加到转矩指令中,则6阶转矩谐波就会消失.与额外转矩对应的q轴补偿电流可表示为

(19)

因此,q轴参考电流包括与平均转矩对应的标称q轴电流iqo、减小转矩脉动的补偿q轴电流iqc:

(20)

3 试验结果分析

图6为本文提出的EPSS永磁同步电动机的转矩控制框图.参考转矩由主控制器根据车辆速度、发动机转速、转矩传感器输出和转向角等信息产生.dq轴参考电流由对应于所需转矩的标称dq轴电流和减小转矩脉动的补偿dq轴电流组成.补偿dq电流取决于转矩大小,它具有6阶谐波电流来抵消6阶转矩脉动.

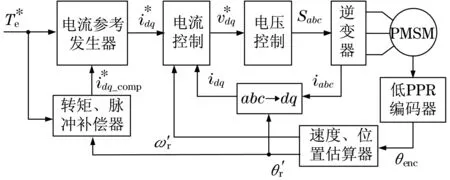
图6 转矩控制方案Fig.6 Torque control scheme

基于估算的转子位置将dq轴参考电流与从定子轴系abc中电流转换来的dq轴电流进行比较.具有比例积分(PI)电流控制器生成dq轴参考电压,通过空间矢量PWM逆变器将对应于dq轴参考电压的三相电压施加到电动机,电机两端直流电压为12 V,通过测量低PPR编码器信号的周期来估算转子速度和转子位置.转子位置估算的转矩控制由DSP TMS320F28335实现,电流指令生成和转子速度计算的控制频率为420 Hz,电流控制频率为1.68 kHz,电压控制的PWM频率为20 kHz.永磁同步电动机有3相6极,永磁体安装在转子磁芯的表面,使d轴和q轴的电感几乎相等.

图7为基于编码器信号的机械角和电度角、估算的转子位置和相电流的变化曲线,图7(a)中电动机转速为50 r/min恒定转速,图7(b)中电动机转速从35 r/min加速至80 r/min,参考扭矩为3.2 N·m,q轴电流为65 A.

由图7分析可知：电动机转速从35 r/min加速至80 r/min时,除了基于估算的转子位置的相电流外,其余参数波形类似,表明估算的转子位置在恒定速度和可变速度下都具有高分辨率.

图8为无转矩脉动补偿电流情况下,电动机由64 PPR编码器信号驱动时的电流和电动机转矩、基于电度角分辨率为16.875°的编码器信号来控制

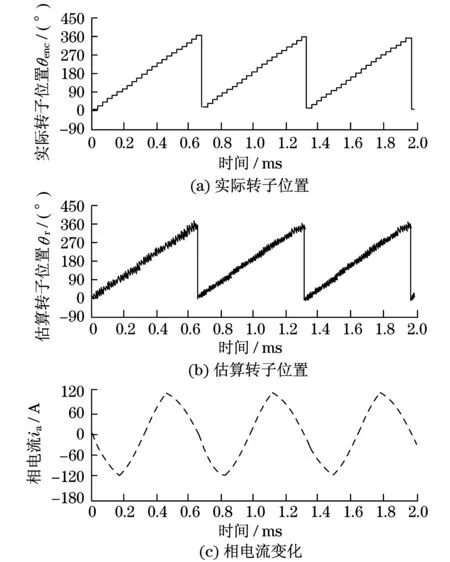
图7 电动机转速50 r/min时实际转子位置和估算转子位置

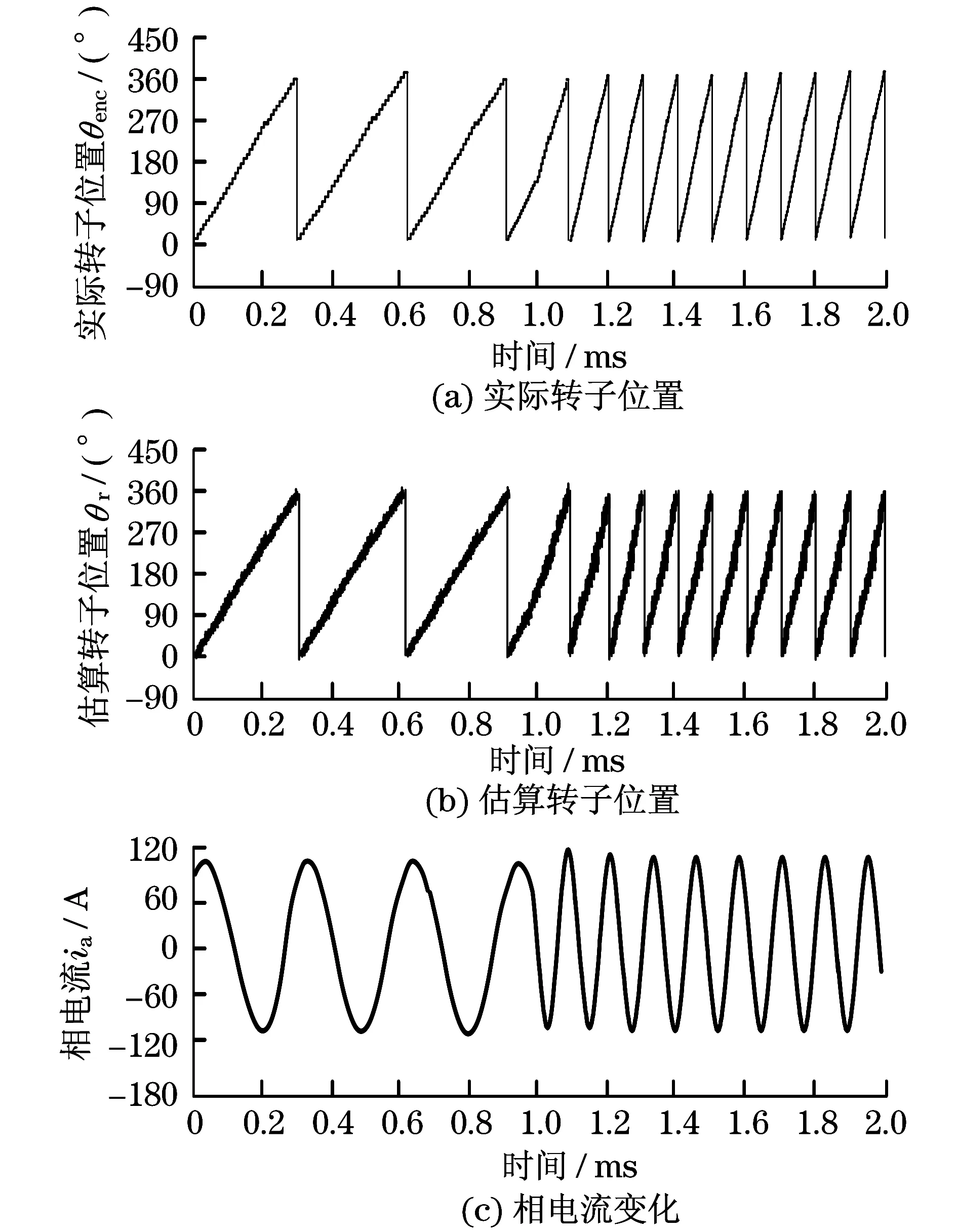
图8 电动机转速35 r/min加速到80 r/min时实际转子位置和估算转子位置

电流,相位电流也由编码器信号进行量化,量化的相电流会在dq轴电流中产生脉动.各影响因素作用使电动机转矩具有高频脉动,转矩脉动峰的峰值为0.2 N·m,是平均转矩的6.25%.如此大的转矩脉动将在汽车方向盘上产生机械振动,并且超出了EPSS的转矩脉动极限.

图9为无转矩脉动补偿电流情况下,电动机由估算转子位置驱动时的电流和电动机转矩.

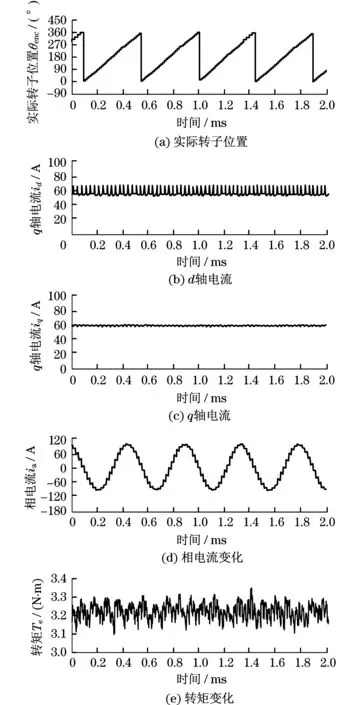
图9 编码器驱动电动机时电流和转矩Fig.9 Current and torque when the encoder drives the motor

由图9可知,dq电流脉动显著减小,并且由于电流由高分辨率的估算转子位置控制,相电流近似正弦波形.由量化的编码器信号引起的高频转矩脉动消失,但其仍然具有因机械不平衡、磁饱和、齿槽转矩等因素引起的固有转矩谐波,转矩脉动峰的峰值约为0.1 N·m,是平均转矩的3.1%,主要成分是6阶谐波.

为了减少电动机转矩的6阶谐波,将转矩脉动补偿器产生的补偿dq轴电流添加到参考dq轴电流中,dq轴电流和补偿q轴电流及电动机转矩如图10、图11所示,补偿q轴电流的大小为1.3 A,约为标称q轴电流的2.0%.补偿q轴电流产生的脉动转矩可以抵消电动机固有的转矩脉动,其峰值衰减为0.05 N·m,为平均转矩的1.6%.

图10 估算转子位置驱动电动机时电流和转矩Fig.10 Estimate the current and torque when the rotor position drives the motor

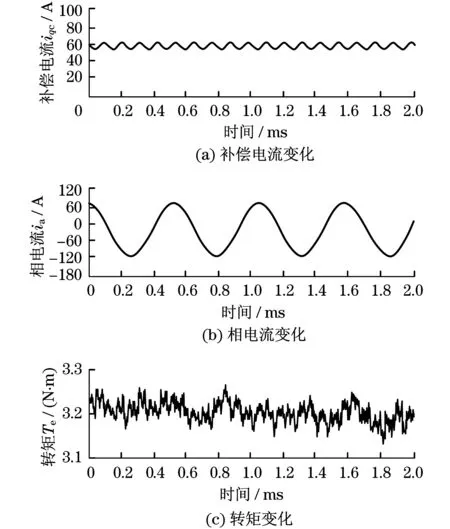
图11 转矩补偿时估算转子位置驱动下的电流和转矩

4 结语

本文提出一种基于低分辨率编码器估算转子位置的方法来减少转矩脉动,分析了编码器分辨率对转矩脉动的影响.根据低分辨率编码器信号估算转子位置,以减少由低PPR编码器量化的转子位置引起的电流谐波.为减小EPSS系统中的转矩脉动,将用于消除6阶转矩谐波的额外q轴电流添加到参考电流中.实验结果表明：通过应用估算的转子位置和转矩脉动补偿,有效地降低了转矩脉动波峰峰值.