强流脉冲离子束表面改性奥氏体不锈钢分子动力学的研究
武志平,徐芳泓,王 岩
(太原钢铁(集团)有限公司,太原 030003)
表面改性能够改变材料的外观、光学性能、摩擦磨损性能、表面组织状态和亲水性[1-4]。高能束辐照在表面改性中得到了广泛应用。例如,离子辐照可以增加Mg合金的表面粗糙度,改变表面合金状态提高抗腐蚀性能[5-6],或者使316L奥氏体不锈钢表面光滑化[7]。因此,离子束辐照是制造和获得各种功能性表面的有效途径。然而,离子束辐照的表面演化过程涉及溅射、热传导和冲击波型能量传递,很难直接通过实验观察获得其过程。采用分子动力学(MD)方法是研究辐照下表面演化过程的有效方法,因其花费较小,已被广泛地用于超高速能量沉积过程,例如在原子水平上具有高空间分辨率的激光-材料相互作用[6,8-9]。奥氏体不锈钢在现代工业领域有着广泛的应用,在核工业中,奥氏体不锈钢作为辐射环境中的压力容器和螺钉被广泛地应用于核反应堆中。奥氏体不锈钢的应用需要可控的表面性能,高能束辐照对奥氏体不锈钢表面改性具有很大的潜力。为了获得所需的部件表面形貌或避免反应堆失效,并使长寿命的核反应堆运行在可控状态下,有必要了解奥氏体不锈钢在辐照下的表面演变过程。本研究选择了奥氏体不锈钢作为研究对象,着重研究辐照条件下表面演化的动力学机理。当高能粒子穿透固体时,它会对所穿过材料的路径附近的原子产生强烈的电子激发。由于高电子迁移率,金属中电荷中性的快速恢复会导致快速放热,引起熔化损伤即热尖峰模型[10]。
1 研究方法
1.1 实验模型
本研究使用的奥氏体不锈钢表面辐照的分子动力学模型由奥氏体不锈钢基体和其表面的平面热尖峰组成,见图1.奥氏体不锈钢晶格为FCC晶格,晶格常数为3.6 nm.在本研究中,所用的盒子尺寸在X,Y,Z方向上分别为72.0,72.0,288.0 nm.试样尺寸在X,Y,Z方向上分别为72.0,72.0,144.0 nm,共包含64 800个原子位置。所有这些位置都由Fe,Cr,Ni原子占据;根据18-10型奥氏体不锈钢的典型成分,Fe,Cr,Ni占据几率分别为72%,18%,10%.采用厚度为7.2 nm的、含4 000个原子的表面层模拟辐照引起的热尖峰。在底部厚度为7.2 nm的区域,每个原子上的位移分量被设置为零,以限制试样的刚性运动。仅在X和Y方向上施加周期边界条件,顶部为自由边界。奥氏体不锈钢中的原子相互作用使用嵌入原子势表示[11]。为了消除由于原子互混而造成的局部高势能位型和应力增大,使用NTP系综(Nose-Hoover热浴)在300 K,0 Pa的条件下使不锈钢基体弛豫15 ps,使其达到平衡状态。然后记录各个原子的位置,以便进行后续模拟。
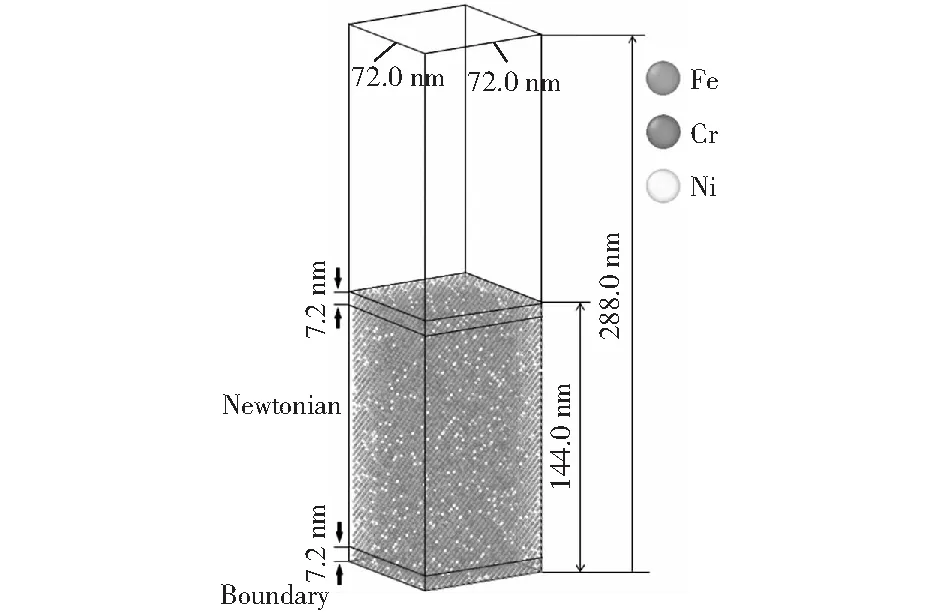
图1 奥氏体不锈钢表面辐照分子动力模型Fig.1 MD model of irradiation on the austenitic stainless steels surface
1.2 计算方法
本文中,对于辐照过程的模拟是在NEV绝热环境下进行的。模拟使用了LAMMPS(large-scale atomic/molecular massively parallel simulator)代码[12]。热峰区域原子的速度分布满足高斯分布,其速度满足
(1)
式中:ETS和N分别是热峰区的能量和原子数量;mn和vn分别是该区域中第n个原子的质量和速度;Ts是设定的热峰区温度;k是Boltzmann常数;ETS等于入射粒子的能量[13]。本研究的热峰区温度范围为5×103~7.0×104K,对应的入射粒子能量范围2.5~35.0 keV.在对每个原子分配速度后,奥氏体不锈钢试样中的原子在NVE系综内继续弛豫100 ps,该时间足以获得平衡状态。使用OVITO代码[14]来表述瞬时样品中原子的位置和速度等信息。
2 实验分析
2.1 辐照过程中的能量演化
热尖峰区的能量传输过程决定了微结构的演化。能量的传递导致了自间隙原子簇或间隙位错环等缺陷的产生。此外,高能状态的表面会产生溅射行为,从而影响辐照样品的形貌。通过MD模拟,得到了在5×103~7.0×104K范围内的初始几ps能量演化过程。图2(a)-(d)为在热尖峰温度为5×103~7.0×104K时,前2 ps原子位置随时间的演化。图2(e)-(h)给出了不同热尖峰温度下平均动能分布的演变过程。为了清楚起见,图中只显示了动能大于0.27 eV的原子,这些原子对应于18-10型奥氏体不锈钢的沸腾温度。根据原子相对于初始表面的位置和能量状态,原子可分为3类,分别对应了热尖峰区的3种能量消耗方式:溅射、导热和冲击波。溅射的特征在图2(a)-(d)中用初始表面以上的原子数和图2(e)-(h)中虚线右侧的平均动能分布来表示。当热尖峰温度低于1.0×104K时,在初始表面以上没有原子,平均动能急剧下降。结果表明,奥氏体不锈钢的溅射要求热尖峰温度至少为1.0×104K,且溅射强度随温度的升高而增加。 冲击波特征由图2(a)-(d)所示的初始表面下的原子和图2(e)-(h)中向基体深处移动的平均动能峰值表示。具有较高热尖峰温度的样品,有着较厚的运动原子平面和更大的向基体深度移动的能峰。原子平面和能量峰都是不对称的,即传播方向的一面较为锋利,相反的一面较为平缓。随着波的传播,其振幅衰减。根据图2(e)-(h)中能峰的位置,冲击波的速度随着热尖峰温度的升高而增加。使用线性拟合通过峰值位置来量化冲击波的速度时间的关系(图3)。当热尖峰温度从5×103K增加到7.0×104K时,速度从6.2 km/s增加到9.3 km/s.这表明热尖峰激发的冲击波以超音速传播,这是由KORCHUGANOV et al[15]在辐照铁晶粒中观察到的。应该指出,图2(c)和(d)中的冲击波是由底部边界反射的。由于底边界原子是固定的,激波的能量保持不变,仅改变了传播方向。因此,Z方向的盒子尺寸不会影响冲击波的行为。与上述两个特征相比,热传导特征难以直接观察到。初始表面的能量不仅受到热传导的影响,还受到溅射和冲击波的影响。然而,在0.5 ps后,它可以获得关于热传导特性的信息。
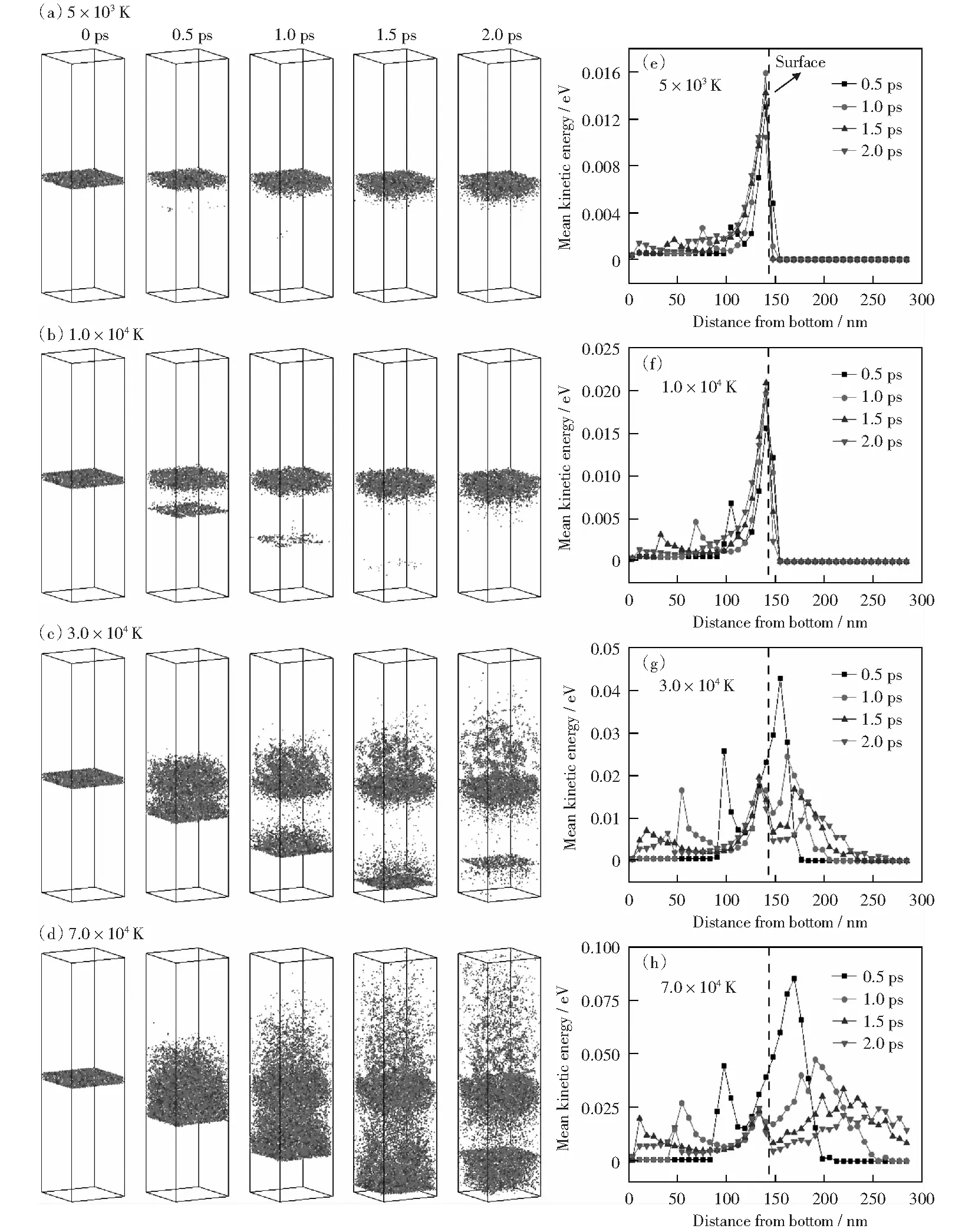
图2 (a)-(d)在热尖峰温度为5×103 K到7.0×104 K前2 ps中,原子位置随时间的演化显示出的由不同热尖峰温度引发的平均动能分布的演化;(e)-(h)平均动能的演化过程和热影响区温度的关系Fig.2 (a)-(d) The evolution of the atomic position via time in the first 2 ps with temperature of thermal spike from 5×103 to 7.0×104 K, (e)-(h) evolution of the mean kinetic energy profile initiated by different thermal spike temperature
在一次模拟过程中,热尖峰只发射了一次冲击波。这意味着冲击波的影响可以在0.5 ps后被忽略。此外,系统的总能量在NVE系综中是守恒的。因此,通过热传导传递到基体的能量等于初始表面附近原子能量的减少,这部分原子包括溅射出表面的原子和残存的原子两部分。如图2(e)-(h)所示,对于所有模拟来说,由初始表面右侧轮廓在0.5 ps之后的面积变化所表示的能量减少可以忽略不计。这意味着热尖峰区与基体之间的热传导在0.5 ps以后可以忽略不计,与模拟初始0.5 ps时忽略的差异相比,当热尖峰温度高于1.0×104K时,保持在表面附近的能量几乎相同。0.5 ps后,由于能量保持在表面附近,并且随着热尖峰温度的升高而以激波形式传播,因此,可以认为溅射和激波在热传导之前消耗了热尖峰区的能量。
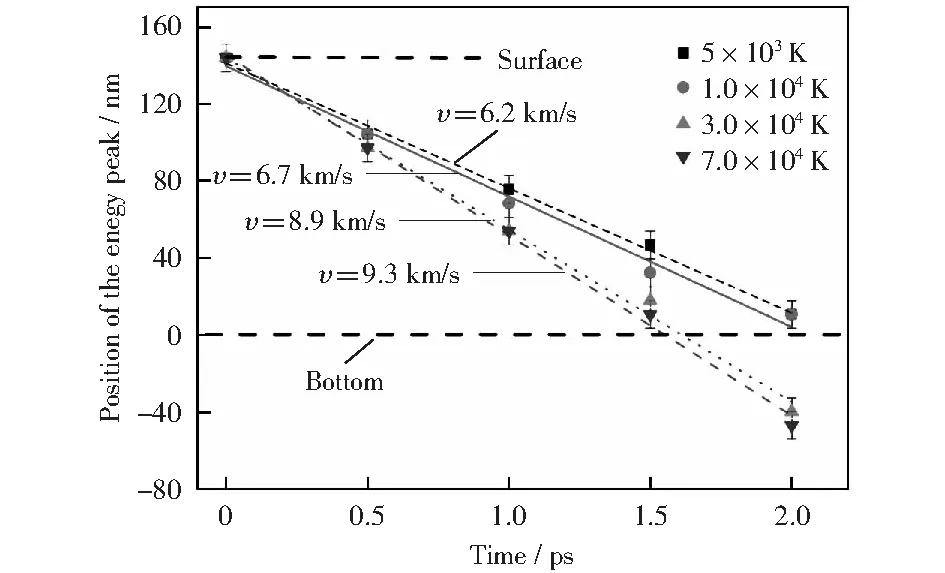
图3 不同热尖峰温度下能量峰值位置随时间变化的关系Fig.3 Relationship between the positions of the energy peak via time for different temperature of thermal spike
根据图2的结果,热尖峰区和基体之间的热平衡以及冲击波形成所需时间要小于0.5 ps.可利用从热尖峰区到基体的能量通量J来说明热尖峰区能量传递的动力学过程。图4显示了在最初的0.28 ps中,在热尖峰温度从5×103K到7.0×104K范围内热尖峰区总能量和J的关系。如图4所示,不同温度所对应的曲线均有相似的形状。如图中的插图部分所示每条曲线被3个点(i-iii)分成四个部分(1-4)。随着热尖峰温度的升高,最大能量通量从1×104eV/ps增加到1.8×105eV/ps.随着热尖峰区的能量传递到基体上,能量通量沿着段1迅速增加,直到达到最大值。然后沿段2到段4下降到几乎为0,其中段3出现能量通量的瞬态增加。段2的斜率几乎与段4相同。能量通量可以使用第2段和第4段描述:
J=aUTS+b.
(2)
式中:a和b为常数,UTS是总的势能和动能之和。热尖峰区和基体的能量是守恒的:
UTS+UM=UB.
(3)
式中:UM是基体的总能量,UB是初始时刻系统的总能量,因此式(2)可化为:
(4)
方程(4)说明段2和段4上的能量通量受热尖峰区与基体间的能量差控制。随着能量从热尖峰区传递到基体,两部分的能量差减小,导致能量通量减小。另一方面,当热尖峰区的能量传输到基体时,由段1和段3表示的能量通量增加。根据原子位置随时间的演化结果,这部分能量通量的增加来自冲击波,这表明类冲击过程中向基体传输的能量通量密度较高[16]。因此可以说明,在HIPIB辐照过程中,表面受辐照区域的能量一部分通过热传导至基体原子而被消耗,另一部分以向基体中传播的激波形式被消耗。激波的贡献可用iii状态偏离单一热传导状态的程度来表示。由于iii点与ii点所对应的热峰区总能量相差不大,因此可用ii状态代替iii状态所对应的单一热传导态。从图4可见,激波的贡献随热尖峰温度的降低而减小,2.0×104K时激波的贡献基本可以忽略。

图4 前0.28 ps热尖峰温度在5×103 K到7.0×104 K范围内的热尖峰区总能量与能量通量J的关系Fig.4 Relationship between the total energy of the thermal spike region and J with thermal spike temperature in the range from 5×103 K to 7.0×104 K in the first 0.28 ps
图5给出了热尖峰能量为7.0×104K的初始阶段系统的总能量(a,f)、动能(b,g)、势能(c,h)、能量通量(d)的时间演化。每条曲线被分成4个阶段,对应于图4中的4个部分。在阶段1中,能量通量迅速增加到与图4中的点i相对应的最大值。根据总能量、动能和势能分布的时间演化,在第一阶段0.014 ps内,动能转化为热尖峰区的势能,当势能达到最大值时,动能达到最小值。在这个阶段,热尖峰区的动能被原子的反冲所消耗[6],并且几乎所有的总能量都集中在尖峰区(图5(a)),能量通量迅速增加(图5(d)).当势能达到最大值时,第2阶段开始。由于总能量从热尖峰区传输到基体,能量通量迅速减小,使得两部分之间的差异减小。在此阶段,动能保持恒定甚至略有增加,而势能和总能量则线性下降,直到0.044 ps.阶段3开始于0.044 ps,结束于0.054 ps,在此阶段,热尖峰区的动能开始降低,势能的降低比阶段2缓慢。能量通量随时间的增加而增加。根据第一阶段和第三阶段的模拟结果,可以得出以下结论:动能向势能的转换使能量通量增加,进而在类冲击过程中导致能量向基体传递的强度更大。第四阶段从0.054 ps开始,动能和势能都随时间而减小,导致能量通量几乎为零。

图5 在热尖峰温度为7.0×104 K的模拟初始阶段总能量(a)(f),动能(b)(g),势能(c)(h)和能量通量(d)的时间演化过程Fig.5 Time evolution of the total energy (a)(f), kinetic energy (b)(g), potential energy (c)(h), energy flux (d) in the initiation of the simulation with the thermal spike energy of 7.0×104 K
2.2 辐照过程中的原子迁移
为了研究辐照条件下表面形貌的演变,记录并分析了原子在厚度为28.8 nm的表面层中的运动。当热尖峰温度超过1.5×104K时,模拟后的表面形貌基本相同。因此,仅研究热尖峰温度为3.0×104K的样品。图6显示了100 ps期间表面层中原子的动能映射。为了清楚起见,只显示模拟之后留在盒子里的原子。从图6中可以看出,表面的粗糙度在前2 ps中增加,并且直到模拟结束才降低。在前2 ps期间,热尖峰的能量传递到表面层中的原子,导致表面处于气体和液体的混合状态。该区域中的大多数原子具有高于0.27 eV(红色原子)的动能并蒸发。由于原子蒸发对熔体表面的湍流有很大影响,因此表面的粗糙度很高。在接下来的4 ps中,蒸发过程逐渐停止,而表面仍然保持液态。由于原子蒸发停止,在液体表面张力的作用下,表面粗糙度降低。在8 ps后的下一个过程中,表面层中原子的动能耗散。表面的状态变成固体,而部分蒸发的原子重新吸附在表面上。这类似在不锈钢基体上沉积不锈钢涂层的工艺。模拟结果说明表面粗糙度受两个因素的影响:一个是原子在表面上的运动,另一个是蒸发原子的再吸附。
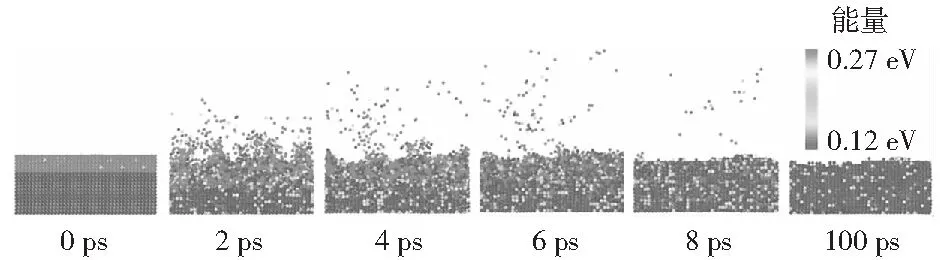
图6 热尖峰温度为3.0×104 K时,表面层中原子在初始100 ps时的动能映射Fig.6 Kinetic energy mapping of the atoms in the surface layer with temperature of thermal spike being 3.0×104 K during first 100 ps
3 结束语
本文基于热尖峰模型,研究了高能离子束辐照下奥氏体不锈钢表面的能量演化和原子传递过程。研究结果表明,奥氏体不锈钢的溅射要求热尖峰温度至少为1.0×104K,且溅射强度随温度的升高而增加。具有较高热尖峰温度的样品具有较厚的运动原子平面和更大的向基体深度移动的能峰。原子平面和能量峰都是不对称的,即传播方向的一面较为锋利,相反的一面较为平缓。随着波的传播,其振幅衰减。冲击波的速度随着热尖峰温度的升高而增加。当热尖峰温度从5×103K增加到7.0×104K时,速度从6.2 km/s增加到9.3 km/s,热尖峰激发的冲击波以超音速传播。在HIPIB辐照过程中,表面受辐照区域的能量一部分通过热传导至基体原子而被消耗,另一部分以向基体中传播的激波形式被消耗。激波的贡献随热尖峰温度的降低而减小,2.0×104K时激波的贡献基本可以忽略。根据对形貌的模拟,表面粗糙度受两个因素的影响:一个是原子在表面上的运动,另一个是蒸发原子的再吸附。

