导爆管等效缩比模型过载特性研究

吴 昊 李明文 惠江海

（1.海军装备部驻西安地区军事代表局 西安 710000）

（2.空军驻包头地区军事代表室 包头 014033）

（3.陆军工程大学石家庄校区 石家庄 050003）

1 引言

引信在战斗部侵彻过程中由于瞬间的相互冲击碰撞而处于复杂的过载环境，利用相关基本理论无法直接推导出引信零件在产生相同变形程度的时其承受过载与其尺寸大小的关系。因此，采用量纲分析法，通过建立量纲方程获得二者之间的抽象函数关系。

量纲分析法基于相似三定理中的第二定理，即Π 定理，该定理的表述如下［1～4］。

设一物理系统有n个物理量，其中有k个物理量的量纲是相互独立的，那么这n个物理量可表示成相似准则 Π1，Π2，…，Πn-k之间的函数关系，其表达式为

针对引信的某个零件，假设其尺寸（内径、外径或长度）为r，在受到过载a时产生变形，则a与r的函数关系如下：

式中：ρ为引信零件材料密度；σ为引信材料特征应力或强度；c为应力波在引信零件材料内部的传播速度；k为引信零件断裂韧性。

将以上三个相似准则代入式（1）即得到引信零件所能承受过载和零件尺寸之间的量纲方程，并将Π2项作为因变Π项，得到量纲方程如下：

2 战斗部侵彻靶板引信零件过载特性

2.1 模型的建立

首先建立战斗部和引信侵彻靶板模型，在战斗部底端加装引信。利用ANSYS/LS-DYNA建立引信和战斗部侵彻靶板有限元模型，采用高强度钢；战斗部壳体采用钛合金材料，靶板与战斗部均采用Johnson-cook材料模型，战斗部装药和引信所有组成零件均采用随动塑性材料模型［5～7］。各材料基本参数如表1所示。

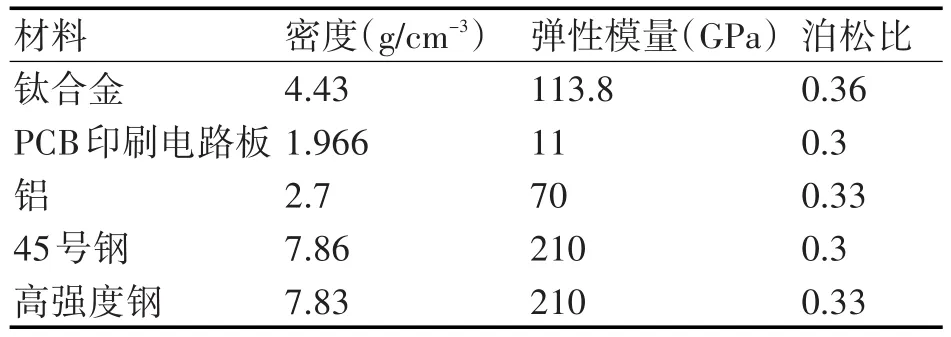
表1 材料基本参数

整个模型均采用solid164实体单元并划分成六面体网格，为了降低仿真计算的时间和所占内存，将整个模型作1/4简化处理。战斗部与靶板之间建立侵蚀接触，引信堵盖与战斗部壳体之间建立固连接触，其余零件与零件之间建立自动接触［8～9］。由于引信零件承受过载的时刻晚于战斗部，因此为了充分获得引信零件的过载特性，将侵彻作用时间设为 800 μs。侵彻初速度设为 1900m/s（5.6Ma）。建立后的引信和战斗部侵彻靶板模型和其网格划分后的有限元模型如图1和2所示。

图1 引信和战斗部侵彻靶板模型

图2 网格划分后引信和战斗部侵彻靶板有限元模型

2.2 过载特性分析

通过仿真得到导爆管壳体的过载特性曲线如图3所示。通过图3曲线可以看出，导爆管壳体在战斗部以1900m/s速度侵彻靶板过程中承受到的侵彻过载峰值（不考虑方向）为77771g。基于导爆管在战斗部侵彻过程中的过载特性，对导爆管进行缩比模型设计。

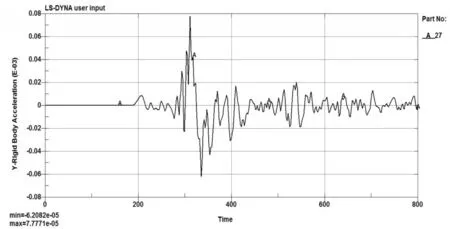
图3 导爆管壳体侵彻过载特性曲线

3 导爆管缩比模型设计

3.1 模型的建立

通过仿真计算得到在导爆管变形率相同的情况下，不同尺寸导爆管壳体所承受的过载值，从而获得导爆管尺寸与其壳体承受过载之间的关系［10～12］。

图4 加载件压缩示意图

将完整的导爆管置于刚性平面，上方置一刚性体。加载示意图如图5所示。导爆管壳体过载变化曲线如图9所示。

图5 导爆管恒力加载示意图

通过图9的结果可以得到使外径为1.2cm的原型尺寸导爆管产生变形率φ=0.35时其壳体临界过载为80124g，高于图3所示的导爆管壳体在战斗部侵彻过程中所受到的侵彻过载峰值77771g，说明在战斗部以1900m/s的速度侵彻靶板的过程中导爆管能够正常工作。

图6 导爆管1/4模型

图7 导爆管发生压缩变形

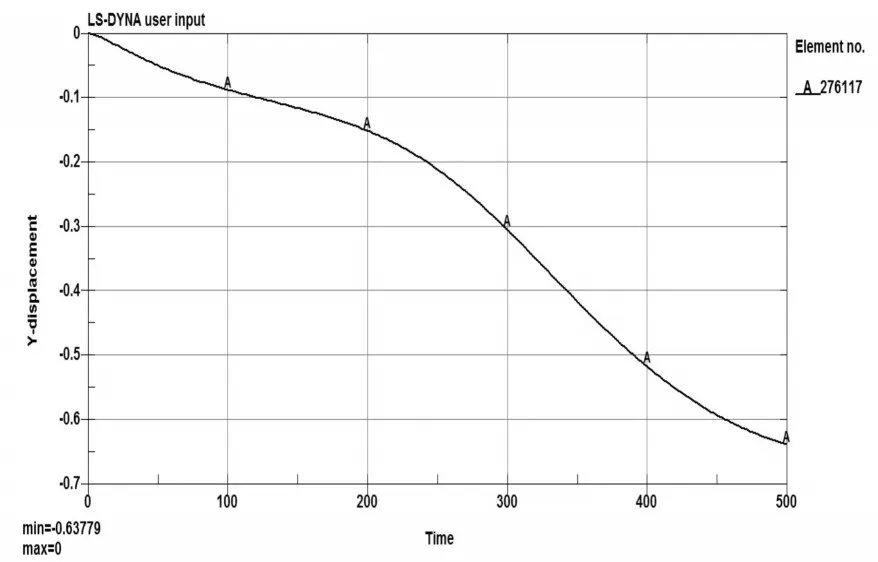
图8 原型尺寸下导爆管压缩量

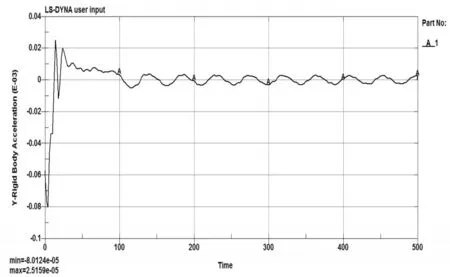
图9 外径1.2cm导爆管壳体过载曲线

3.2 不同尺寸下导爆管壳体临界过载

依次对外径为 1.1cm、1.0cm、0.9cm、0.8cm、0.7cm、0.6cm、0.5cm、0.4cm的导爆管建模并仿真计算。分别得到8种不同尺寸导爆管产生变形率φ近似等于0.35时其壳体所承受的过载变化曲线如图10（a）～（h）所示。

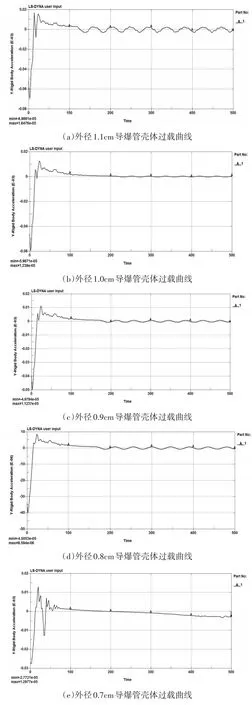
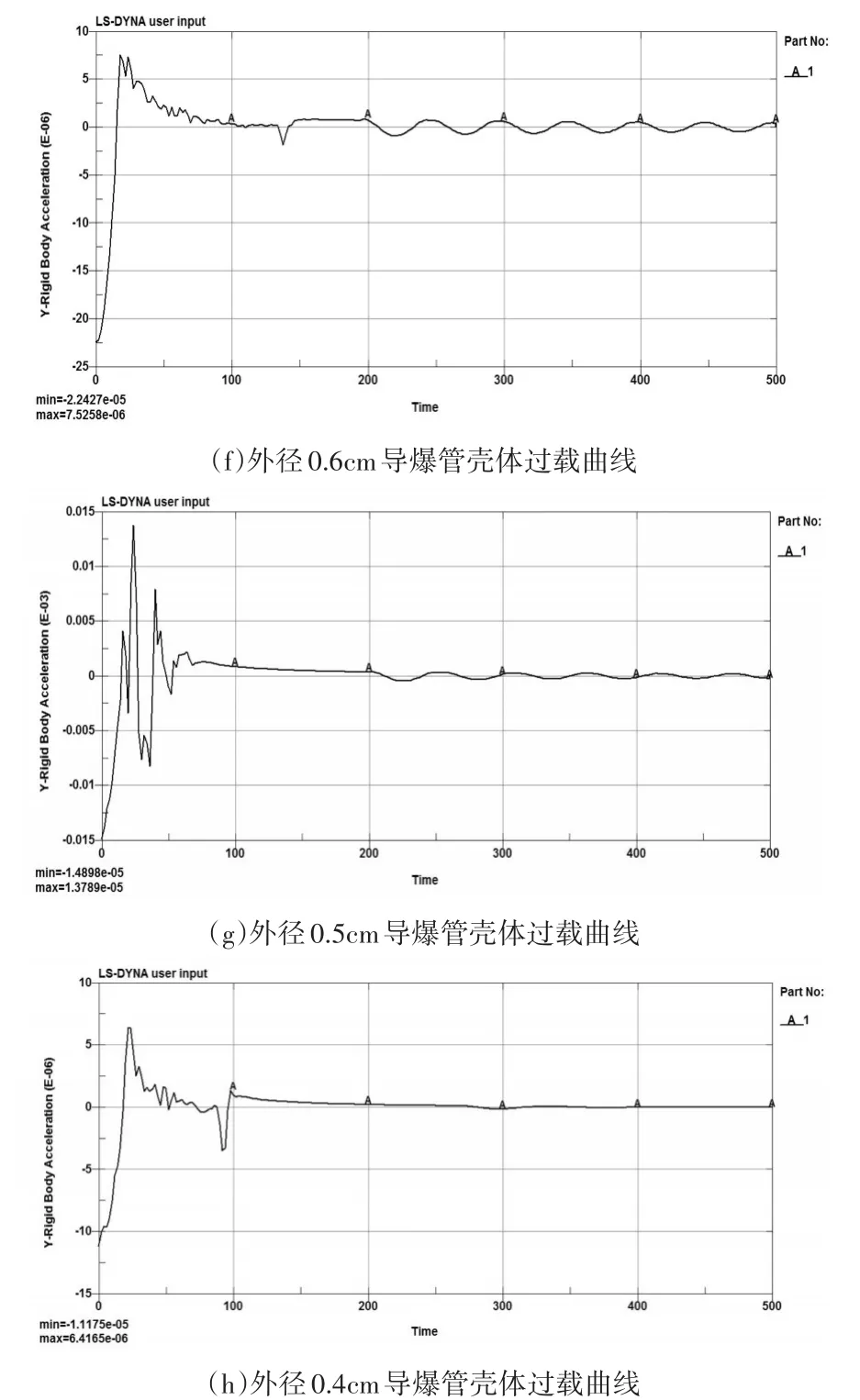
图10 不同尺寸导爆管壳体过载曲线

3.3 导爆管尺寸与其壳体临界过载的关系

根据图10所示的8种不同尺寸导爆管壳体过载曲线，分别取过载曲线的最大值即为所定义的导爆管壳体临界过载（不考虑方向），再加上由图9所示原型尺寸导爆管壳体的临界过载，将9种不同尺寸导爆管壳体的临界过载以及相应的压缩量和变形率列表如表2所示。

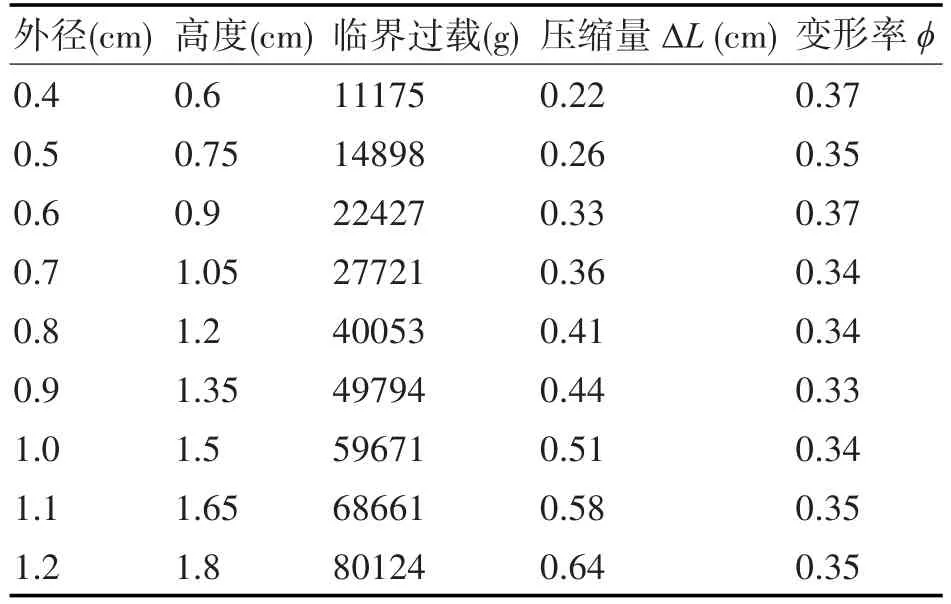
表2 不同尺寸导爆管壳体临界过载及所对应压缩量和变形率

由表2可以看出不同尺寸导爆管的变形率不全相同，但由于变形率之差引起的压缩量之差相比导爆管尺寸可以忽略不计，故将导爆管的变形率近似看作相同。

将导爆管外径作为横坐标，临界过载作为纵坐标，则9个外径和临界过载所组成的坐标点描绘在坐标系中如图11所示。

图11 导爆管外径与其壳体临界过载坐标点

观察图11所示导爆管壳体临界过载随外径的变化趋势，采用傅里叶拟合将9个点拟合出导爆管外径尺寸与其壳体临界过载的函数关系曲线如图12所示，其中函数自变量是导爆管外径，因变量是导爆管壳体临界过载。

图12 导爆管尺寸与其壳体临界过载的函数关系曲线

拟合得到的函数如下：

a=55680-38770cos（2.248r）-26190sin（2.248r）（4）式中，a、r为导爆管壳体临界过载和导爆管外径，且0.4≤r≤1.2。

式（4）即为所得到的导爆管尺寸与其壳体临界过载的关系，在缩比模型试验中得到导爆管壳体临界过载，即可由式（4）估计出在产生相同变形率的情况下其原型尺寸导爆管壳体临界过载的大小。

4 结语

1）采用截枣核形战斗部建立引信和战斗部有限元模型，并以1900m/s的速度侵彻靶板，获得导爆管壳体的过载特性曲线和承受冲击过载峰值。

2）按比例设计了导爆管缩比模型并仿真计算得到导爆管缩比模型在产生塑性应变时承受的过载峰值，通过傅里叶拟合获得导爆管在产生塑性应变时承受的过载峰值与其尺寸大小的关系。