空间光通信中光源相干参数对接收光强影响研究

李梦男,鲁文帅

(中国电子科学研究院，北京 100041)

0 引 言

随着信息时代高速发展，空间通信传输数据量需求剧增，激光通信技术可以满足由于军事侦察、地震预报、海洋观测、环境保护和深空探测等所产生的巨大数据传输量需求。激光通信具有通信容量大、传输带宽高、抗电磁干扰能力强、安全保密性好、终端体积小和功耗低等众多优点，由于在商业和军事上具有诸多潜在的优势，各国的研究人员都竞相致力于激光通信的技术开发[1-4]。

在实际光通信过程中，受光学元件表面加工误差、光学系统装调误差及空间环境的影响，并且激光器自身的缺陷等均使得由光学天线出射的激光光束通常不是理想的完全相干光源，而是以部分相干光的形式存在，且表现为高斯-谢尔模型[5-6]。Ricklin等推导出了自由空间中部分相干光源的光强闪烁指数和孔径平滑因子，并得到了空间光通信系统的误码率[7-10]。然而该项研究工作中，仅考虑了空间光通信中光源相干参数对光强起伏的影响，没有涉及光源相干参数对平均接收光强的影响，因而没有得出实际光通信链路中的接收光强概率分布。

目前，通常采用尽量增大链路冗余的方法来弥补大气湍流及光源相干度下降等因素引起的系统接收光强的衰减。在空间光通信系统中，适当的增加激光器的发射能量相对容易许多，因此量化光源相干度下降引起的接收光强衰减，精确的获得由各种因素对系统接收光强产生的影响具有一定的现实意义。

1 光源相干参数对平均接收光强影响

在实际光通信过程中，受到传输路径中大气湍流的影响，传输光束随着传输距离的增加会产生光束展宽。不同光源相干参数的光束展宽会发生变化，使得系统平均接收光强发生变化。由文献[11]可得高斯-谢尔光束传输平面z处的交叉谱密度函数W(r1,r2,z)的表达式，即

(1)

式中的参数为：

(2)

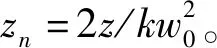
在自由空间中，由交叉谱密度函数理论，传输路径上平面z>0处的平均接收光强定义为I(ρ,z)=W(ρ,ρ,z)。经过整理，平均接收光强可以表示为

式中参数wp(z)为高斯-谢尔光束在大气湍流影响下接收端处光束的束宽，且wp2(z)=w02L(z)。

表1给出了本节仿真中用到的参数。在自由空间中，为了清楚的表述光源相干参数对平均接收光强的影响，选取大气湍流下传输最远距离z=10 km。

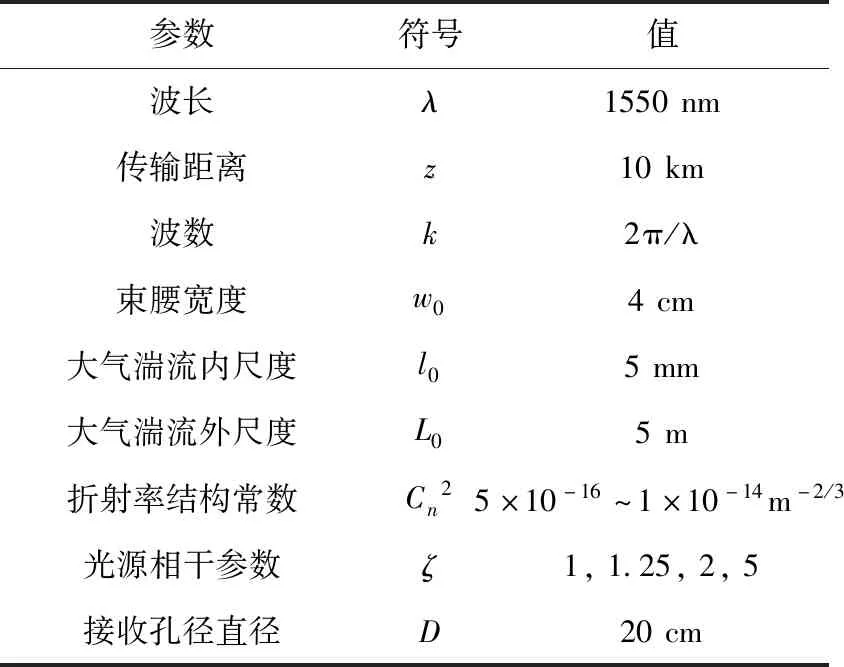
表1 空间光通信中仿真参数

图1给出了传输距离z=10 km时，不同大气湍流强度与光源相干参数下，归一化平均接收光强分布。采用Cn2=5×10-16m-2/3且光源相干参数ζ=1条件下的平均中心光强对系统平均接收光强进行归一化处理。

从(a)图可以看出，随着光源相干参数的增大，平均接收光强降低且接收端处光束的束宽增加。相对而言，光源相干参数越大，靠近光束中心处的平均接收光强越小，而远离光束中心处的平均接收光强则越大。例如，当光源相干参数ζ分别取值为1、1.25、2、5时，相对应的平均中心光强值为1、0.8499、0.5859、0.2613，呈现为减少的趋势。当选取远离光束中心处的平均接收光强时，如ρ=0.2m，相对应的平均接收光强值分别为0.02433、0.03613,0.06641、0.09896，呈现为增加的趋势。同样在图(b)至(d)中可以得出类似的结论。

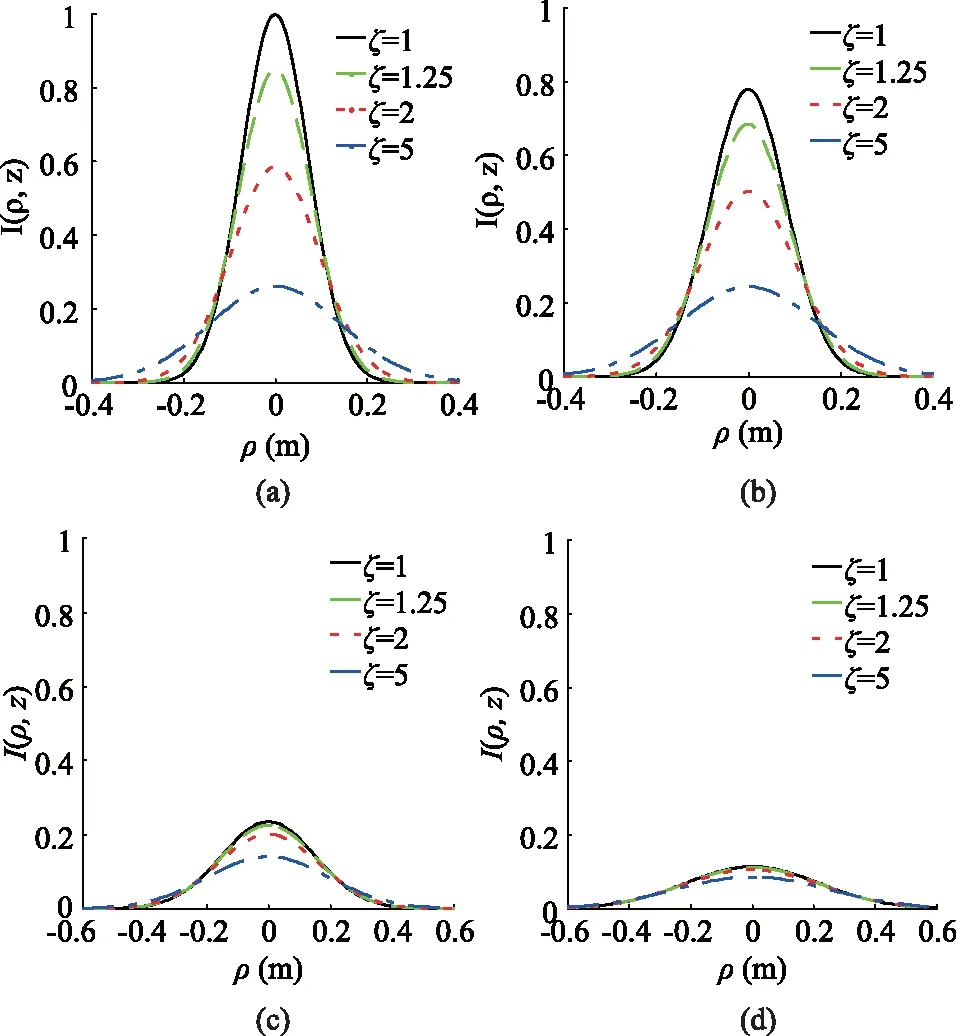
图1 不同光源相干参数下，归一化平均接收光强分布(a) Cn2=5×10-16 m-2/3 (b) Cn2=1×10-15 m-2/3(c) Cn2=5×10-15 m-2/3 (d) Cn2=1×10-14 m-2/3

图2给出传输距离z=10 km时，不同大气湍流强度下的平均中心光强随光源相干参数的变化曲线。采用Cn2=5×10-16m-2/3且光源相干参数ζ=1条件下的平均中心光强对系统平均接收光强进行归一化处理。

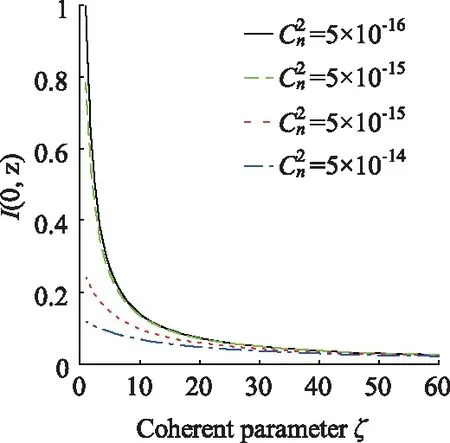
图2 不同大气湍流强度下，归一化平均中心光强随光源相干参数的变化曲线

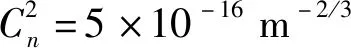
对比四条曲线的平均中心光强值可以得出，随着光强相干参数的增加，四条曲线从发散状态转为汇聚状态。即随着光源相干参数的增加，平均中心光强的差值减小。当光源相干参数较大，如ζ=60时，四条曲线汇聚在一起，此时平均中心光强受大气湍流强度的影响非常小。

图3给出传输距离z=10 km时，不同光源相干参数下的平均中心光强随大气湍流强度的变化曲线。采用Cn2=1×10-16m-2/3且光源相干参数ζ=1条件下的平均中心光强对系统平均接收光强进行归一化处理。

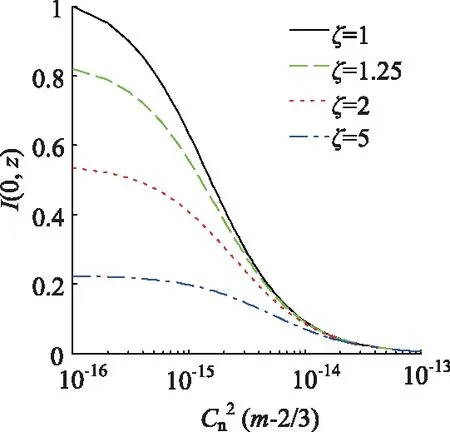
图3 不同光源相干参数下，归一化平均中心光强随大气湍流强度的变化曲线

从图中可以看出，不同光源相干参数下的平均中心光强曲线随着大气湍流强度的增加，均呈下降趋势。当光源相干参数较小时，大气湍流强度对平均中心光强的影响较大。例如当ζ=1时，平均中心光强曲线总是随着大气湍流强度的增加迅速的下降。随着光源相干参数的增大，曲线随大气湍流强度下降的速度减慢。而当ζ=5时，平均中心光强曲线则总是随大气湍流强度的增加缓慢的下降。

对比四条平均中心光强曲线可以得出，随着大气湍流强度的增加，光源相干参数对平均中心光强的影响减小。如图四条曲线从发散状态转为汇聚状态。即随着大气湍流强度的增加，平均中心光强的差值减小。当大气湍流强度很大，如Cn2=1×10-13m-2/3时，四条曲线汇聚在一起，此时平均中心光强受光源相干参数的影响非常小。

2 光源相干参数对接收光强概率分布影响

部分相干光源在自由空间中传输时，大气湍流的影响将导致接收孔径处的光强随机起伏，不考虑系统自身指向偏差及光束漂移，在弱起伏条件下，接收孔径处光强的概率密度服从对数正态分布，可以表示为[10]

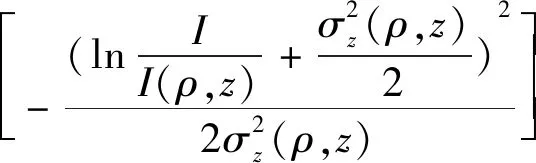
(3)

式中，I(ρ,z)为距离接收孔径中心ρ处的平均接收光强，σz2(ρ,z)为距离接收孔径中心ρ处的光强闪烁方差。

自由空间中，光通信接收孔径处接收光强概率分布同时受平均接收光强和光强闪烁的共同影响。当发射天线出射的光源为部分相干光时，应综合考虑光源相干参数对上述两者的影响。考虑大气湍流的影响，本节将研究光源相干参数对接收光强概率分布的影响。

由上节结论可知，不同光源相干参数下的平均接收光强会发生变化。因此在这里我们将公式(2)代入到公式(3)，可以推导出自由空间中基于部分相干光源的接收光强概率密度函数

(4)

对于部分相干的高斯-谢尔模型光源，根据有效参数法和Rytov近似理论，大气湍流弱起伏下的光强闪烁指数σz2(ρz)可以表示为[12]

(5)

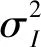
(6)

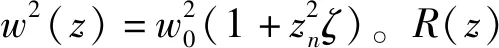
(7)

在光通信接收端，系统接收孔径的平滑效应会降低光强闪烁指数，应考虑孔径平滑因子的影响，因此接收孔径处光强的闪烁指数应表示为Aσz2(ρ,z)，其中A为具有任意空间相干度光束的孔径平滑因子，其可以表示为[7-10]

[cos-1(x)-x(1-x2)1/2]。

(8)

上式中参数D为接收孔径直径。

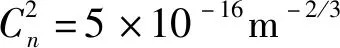
从(a)图中可以看出，随着光源相干参数的增大，中心接收光强的概率分布曲线均向着光强小的一侧偏移。且随着偏移量的增加，中心接收光强会更加集中的分布在平均接收光强两侧，使得中心接收光强的概率峰值增大。例如，当光源相干参数分别取值为1、1.25、2、5时，相对应的中心接收光强概率峰值为1.111、1.288、1.824、3.977，呈现上升趋势。产生该现象的原因为，随着光源相干参数的增大，基于部分相干光源的平均接收光强降低且闪烁指数同样减小，由光源相干参数增大导致的平滑效应使得光强随机起伏程度下降，在图中即表现为更加集中的分布在平均接收光强的两侧。相类似的结论同样可以在图(b)至(d)中得出。

从(a)至(d)对比可以看出，随着大气湍流强度的增加，相同光源相干参数下的中心接收光强的概率分布曲线向着光强小的一侧偏移，并且更加集中的分布在平均接收光强的两侧，同样中心接收光强的概率峰值增大。例如，当光源相干参数ζ取值为1.25时，四幅图所对应的中心接收光强概率峰值分别为1.288、1.515、6.468、9.098，呈现上升趋势。

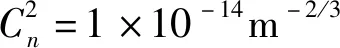
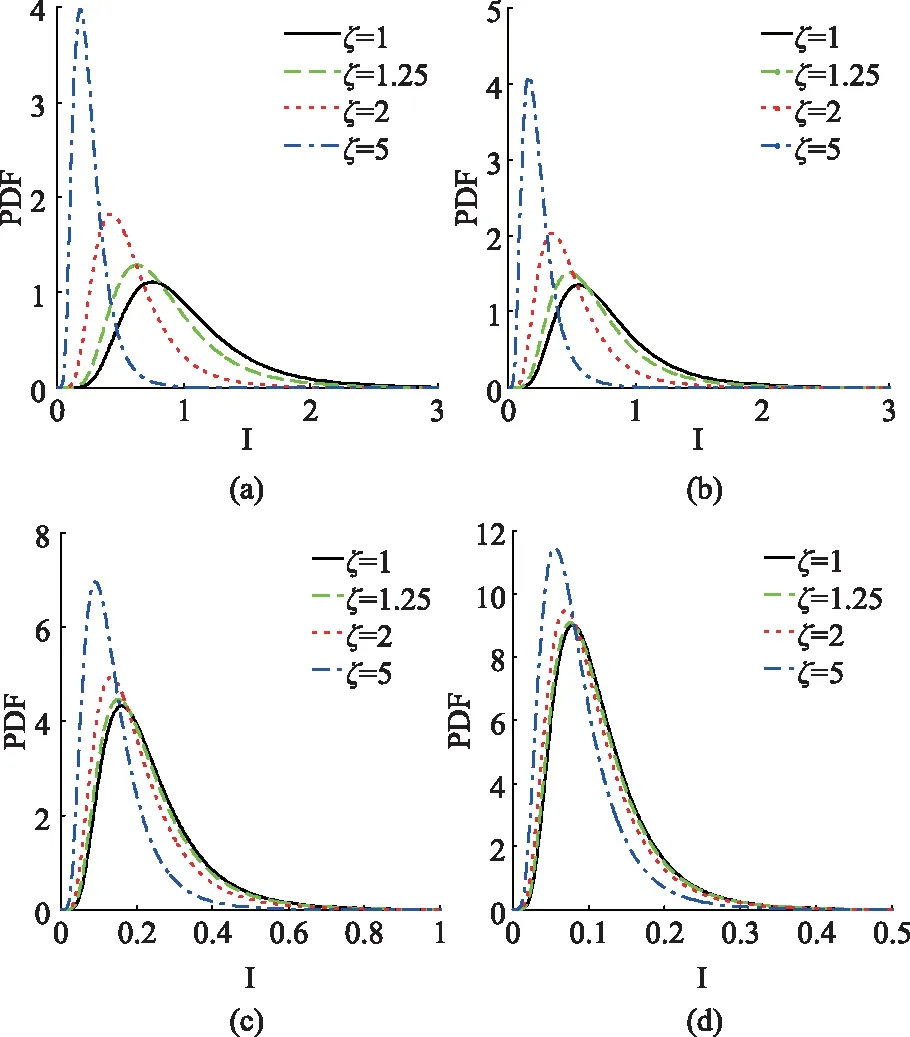
图4 不同大气湍流强度与光源相干参数下，中心光强的概率分布

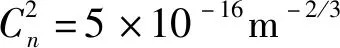
图5 中心光强的概率峰值随光强及光源相干参数的变化曲线

3 结 语

本文综合考虑了空间光通信中光源相干参数变化引起的平均接收光强及光强闪烁指数的变化，给出了基于部分相干光源的接收光强概率分布模型。仿真结果表明，增加了对光源相干参数的考虑，接收系统入射光强发生变化。大气湍流影响下，光源相干度的下降将进一步加剧接收光强的衰减。完全相干光源在大气湍流中传输时，会发生光束展宽及光强随机起伏。随着湍流强度的增大，平均接收光强下降，接收光强的概率分布曲线向光强较小的一侧偏移，且随着偏移量的增加，接收光强会更加集中的分布在平均接收光强两侧，使得接收光强的概率峰值增大。而光源相干参数对接收光强的影响则表现为，随着光源相干参数的增大，光束展宽的增大使得平均接收光强进一步下降。与此同时，接收光强的概率分布曲线表现为同大气湍流强度增大相近的结果。相同大气湍流强度下，随着光源相干参数的增大，接收光强的概率分布曲线的偏移加剧。

在空间光通信中，系统的接收光强是一个非常重要的参量，直接影响着通信系统性能。在采用阈值探测器(APD和CCD)的直接探测接收系统中，当天线的接收光强大于阈值时，探测器可以接收到信号光，而当天线接收光强小于阈值时，探测器不能接收到信号光。在实际空间光通信过程中，除了受大气湍流的影响外，光源相干度的下降进一步加剧了系统接收光强的衰减。目前，通常采用尽量增大链路冗余的方法来弥补各种因素引起的系统接收光强的衰减。因此在空间光通信系统冗余设计时，应综合考虑大气湍流及光源相干参数的共同影响，量化并精确的获得其对系统接收光强产生的影响。本文得出的接收光强概率分布模型，在空间光通信研究中具有一定的实用价值。