基于等效电路模型的超声波电动机匹配电路研究

高炳东，潘云华，张丛巨，王红茹，王 帅

(1．北京自动化控制设备研究所，北京 100074；2．西安创联超声波电动机有限责任公司，西安 710075)

0 引 言

超声波电动机是一种新型运动控制部件，在小型无人机、微型导弹等小功率制导武器领域的成功应用，改善了舵系统体积、质量、快速性、控制精度、电磁干扰等方面的特性，对武器装备控制系统发展具有重要意义。

超声波电动机转速控制变量为驱动电压频率、幅值和两相相位差[1]。对控制系统而言，一般希望控制变量是解耦的，即控制变量能独立可调。然而，超声波电动机LC匹配电路的电压增益易受驱动电压频率和温度影响，从而造成调频调速方式下的超声波电动机的驱动电压频率和幅值发生耦合。

为此，在LC匹配电路的基础上[2-3]，LCC匹配电路[4]、LLCC匹配电路[5-6]及带能量反馈的LC匹配电路[7]得以研究与应用。

本文基于电机等效电路模型，通过计算分析了温度和频率对超声波电动机LC匹配电路、LCC匹配电路和LLCC匹配电路的电压增益的影响，提出了一种带反馈回路的LC匹配电路，实现了转速控制变量解耦。

1 超声波电动机等效电路模型

超声波电动机可以用如图1所示的等效电路模型表示[8-9]，它包括了压电陶瓷片的逆压电效应、定子的强迫振动、定转子间的摩擦和外界负载作用等过程。

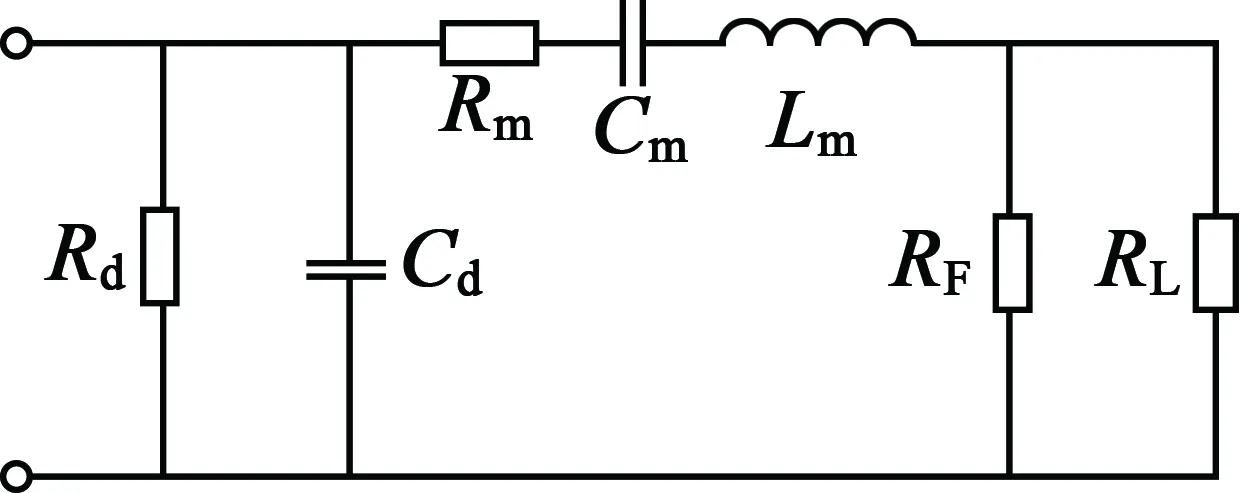
图1 超声波电动机等效电路模型

图1中，Rd和Cd表示压电陶瓷片能量转换过程，其中Rd为损耗等效电阻，表示电损，Cd为静电容，表示存储电荷能力。Lm，Cm和Rm构成定子强迫振动模型，影响机械谐振增益，其中Lm为定子质量效应的等效电感，表示存储动能的能力；Cm为定子弹性效应的等效电容，表示存储弹性势能的能力；Rm为定子机械损耗的等效电阻，表示机械损耗。另外，RF表示定、转子之间的摩擦损耗；RL表示负载作用。

通过对电机等效电路模型分析可知，若忽略定子对压电陶瓷片微弱的压电效应，则与驱动信号存在电气连接的部分只有压电陶瓷片的损耗等效电阻Rd和静电容Cd[10]。因此为方便研究匹配电路，超声波电动机等效电路模型简化为图2，为后续提供研究基础。

图2 电机简化等效电路模型

2 LC匹配电路及其电压增益特性

2.1 LC匹配电路

LC匹配电路是把匹配电感与超声波电动机的容性压电陶瓷片串联或并联，是目前应用最广泛的超声波电动机匹配电路方案。以串联情况为例，如图3所示，其谐振频率：

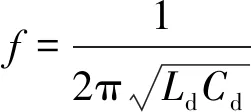
(1)

系统传递函数：

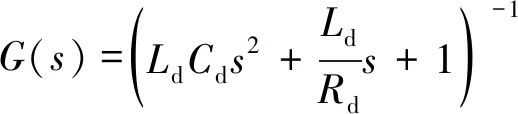
(2)

图3 LC谐振电路

幅频特性函数：

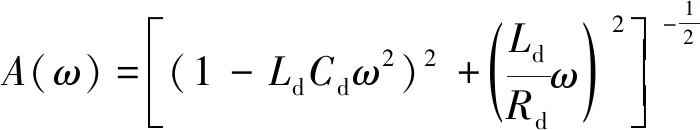
(3)

改为以频率作为自变量的函数：

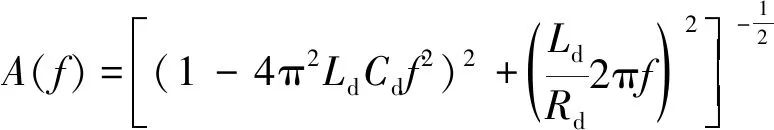
(4)

2.2 温度和频率对LC匹配电压增益的影响

本文选用超声波电动机USM-60，在常温(25 ℃)下，电机工作温升至30～70 ℃，稳定工作驱动电压频率范围为38.5～41.5 kHz。在空载常温下，实测得：Rd= 1.8 kΩ，Cd= 4.5 nF。

当LC电路工作在谐振频率时，电压增益达到最大值，但电压增益随频率变化剧烈。为了使电压增益保持相对恒定且减小附加电感体积，按照经验，令匹配电路谐振频率比驱动电压频率大10～15 kHz，由此确定Ld= 1.7 mH，代入式(1)，得到25 ℃下的谐振频率：

f25 ℃=55 kHz

(5)

在Rd和Ld对温度不敏感[11]的情况下，对静电容Cd的测试表明：Cd呈现明显的正温系数特性，实测曲线和拟合结果如图4所示。

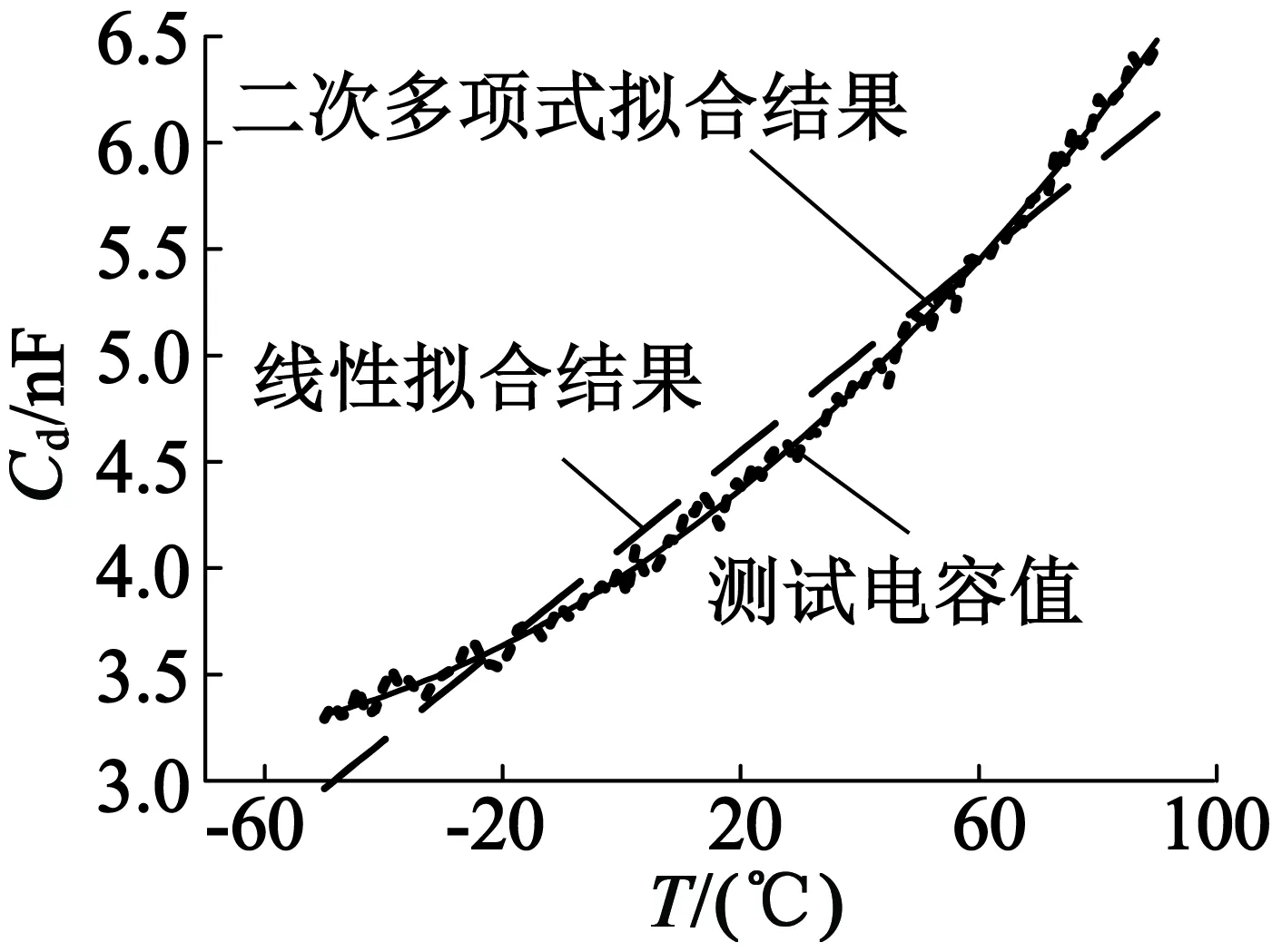
图4 Cd温度特性曲线

其中，一次多项式拟合的结果拟合度R2为0.907 31，二次多项式拟合的结果拟合度R2为0.996 48，二次多项式拟合度适宜，因此选用二次多项式拟合结果，电容值表达式：

Cd(T)=1×10-4T2+0.019T+3.958

(6)

将式(6)代入式(4)，得到电压增益A与温度T和驱动电压频率f的关系式A(T，f)，在30～70 ℃和38.5～41.5kHz的区间内对应曲线如图5所示.以f=38.5 kHz为例，T从30 ℃增到70 ℃时，A由1.70增大至2.07，增幅为21.8%；以T=70 ℃为例，f从38.5 kHz增到41.5 kHz时，A由2.07增大至2.41，增幅为16.4%。

图5 LC匹配电路电压增益与温度和

因此，LC匹配电路电压增益易受驱动电压频率和温度影响。

3 LCC与LLCC匹配电路

LC匹配电路电压增益易受驱动电压频率和温度影响，这使得转速的控制变量驱动电压频率和幅值产生耦合，极不利于电机控速[12-13]。因此，针对这些问题，LCC匹配电路和LLCC匹配电路得到研究与应用。

3.1 LCC匹配电路

LC匹配电路电压增益易受温度影响的原因在于静电容Cd的正温系数特性，因此，在电机端串联一个具有低温漂系数的附加电容CE后再进行LC匹配电路设计，有利于改善谐振电路的温度特性。其模型如图6所示。

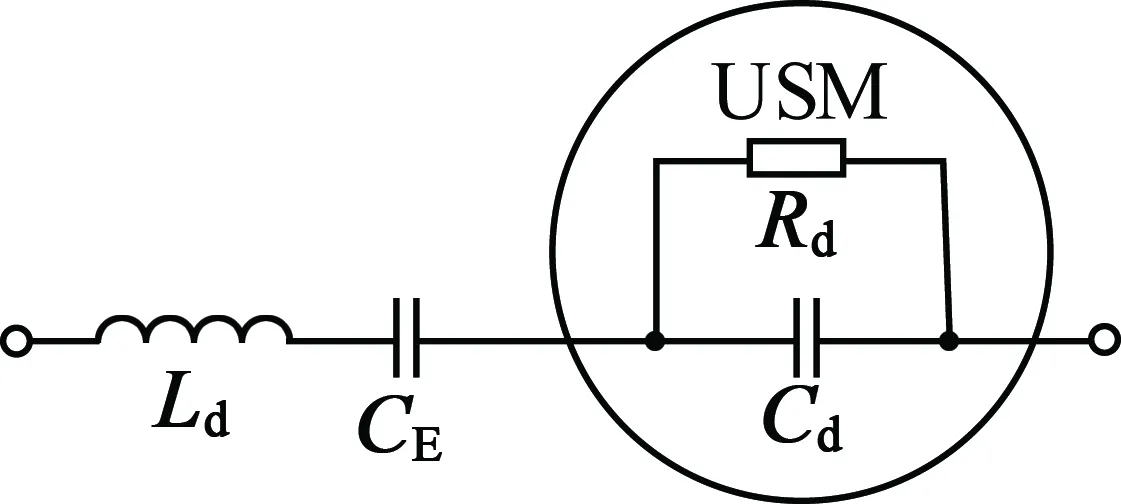
图6 LCC匹配电路

其谐振频率：

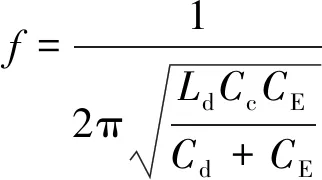
(7)

系统传递函数：

(8)

幅频特性函数：

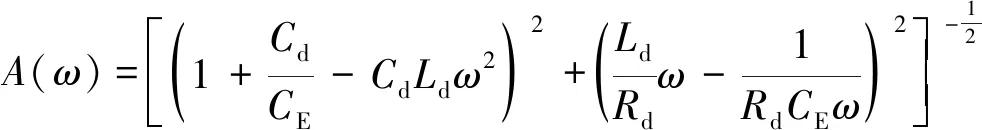
(9)

改为以频率作为自变量的函数：

以选用CE=Cd=4.94 nF为例，以式(7)确定外加电感Ld=3.4 mH。

将式(6)代入式(10)，得到电压增益A对温度T和驱动电压频率f的关系式A(T，f)，在30～70 ℃和38.5～41.5 kHz的区间内对应曲线如图7所示。以f=38.5 kHz为例，T从30 ℃增到70 ℃时，A由0.983减小至0.979，减幅为0.41%；以T=70 ℃为例，f从38.5 kHz增到41.5 kHz时，A由0.979增大至1.19，增幅为21.6%。

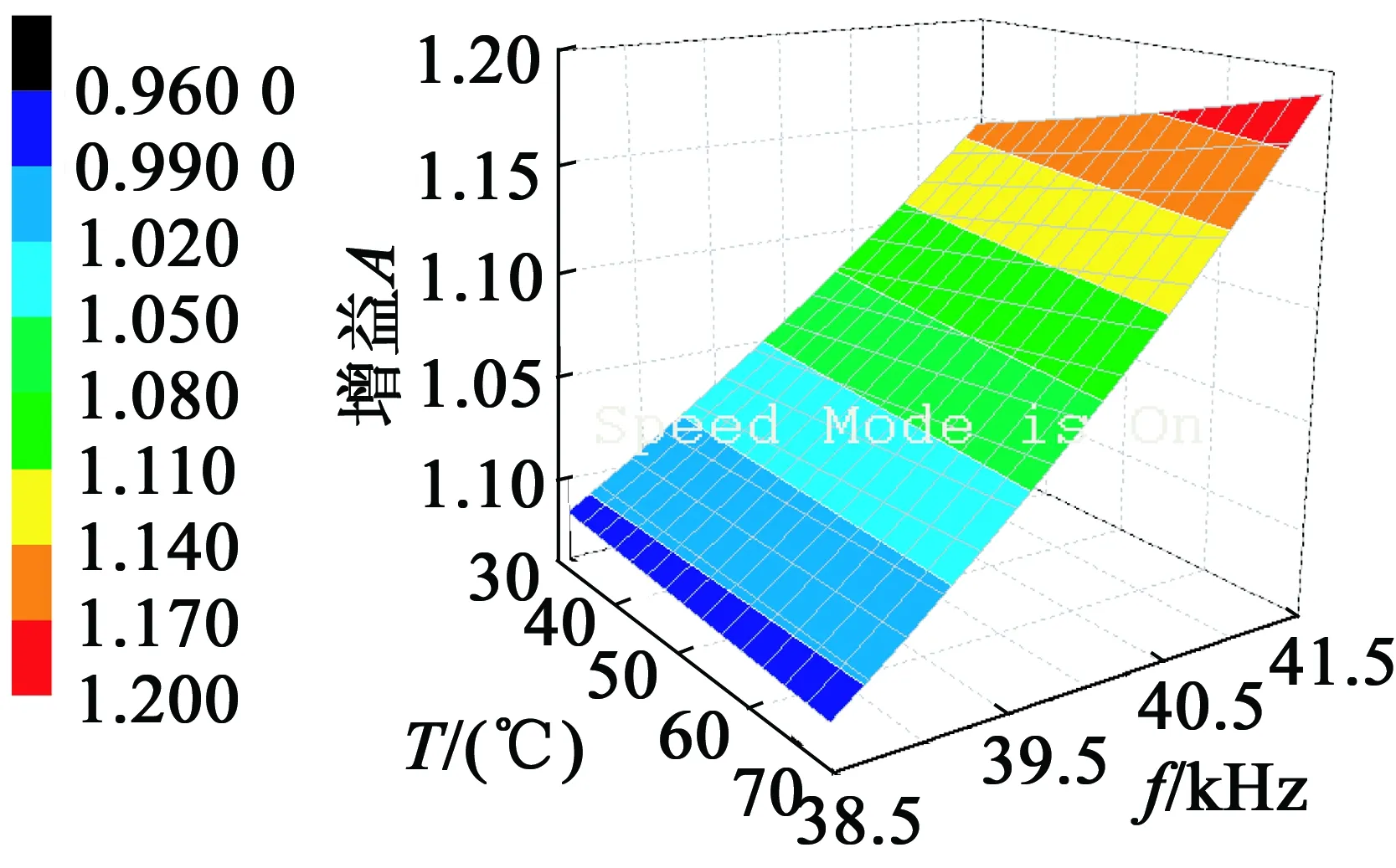
图7 LCC匹配电路电压增益对温度和

对比可知，LCC匹配电路电压增益基本不受温度影响，但仍易受驱动电压频率影响。

3.2 LLCC匹配电路

在LCC匹配电路的基础上，在附加电容CE上再并联一个电感LE，即为LLCC匹配电路，其模型如图8所示。

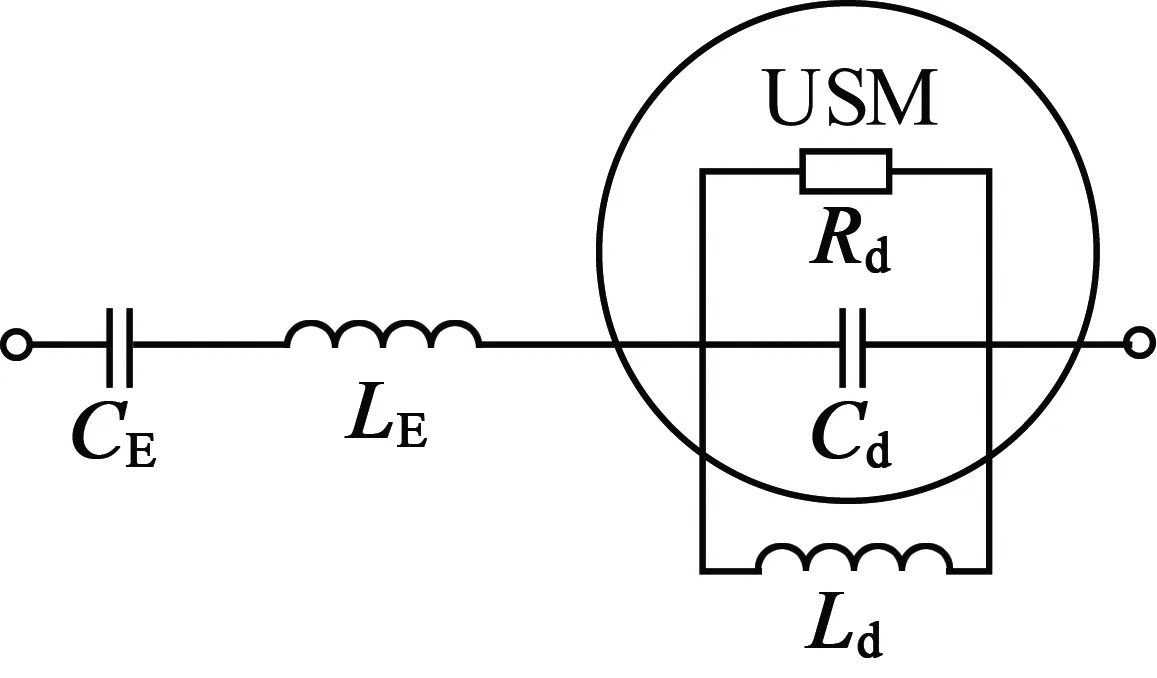
图8 LLCC匹配电路

其电容电感值按下式选择[6]：

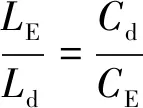
(11)

系统传递函数：

幅频特性函数：

改为以频率作为自变量的函数：

当谐振时，式(13)的实部为1，即：

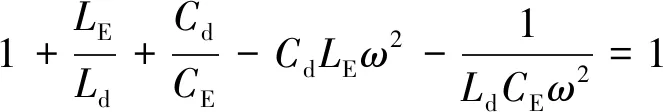
(15)

解式(15)，可得LLCC电路的谐振频率分别如下：

(16)

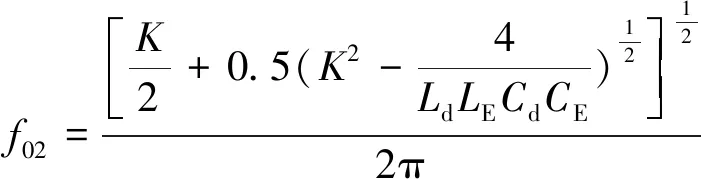
式中：K=(CE/Cd+Ld/LE)/(LdCE)。

定义几何谐振频率fg：

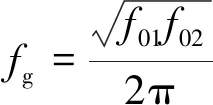
(18)

将式(11)、式(16)和式(17)代入式(18)，得：

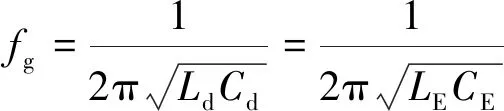
(19)

当驱动电压频率为几何频率fg时，G(s)=1，工作在fg附近时，电压增益达到最大，且匹配电路的幅频特性变化很小[4,6,14]。

选定fg为工作驱动电压频率范围38.5～41.5 kHz的中点值40 kHz，则可得：

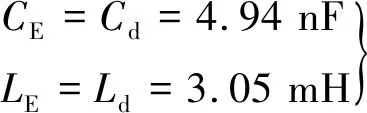
(20)

将式(6)代入式(14)，得到电压增益A对温度T和驱动电压频率f的关系式A(T，f)，在30～70 ℃和38.5 ～41.5 kHz的区间内对应曲线如图9所示。以f=38.5 kHz为例，T从30 ℃增到70 ℃时，A由1.023减小至0.994，减幅为2.8%；以T=70 ℃为例，f从38.5 kHz增到41.5 kHz时，A由0.994增大至1.004，增幅为1.0%。

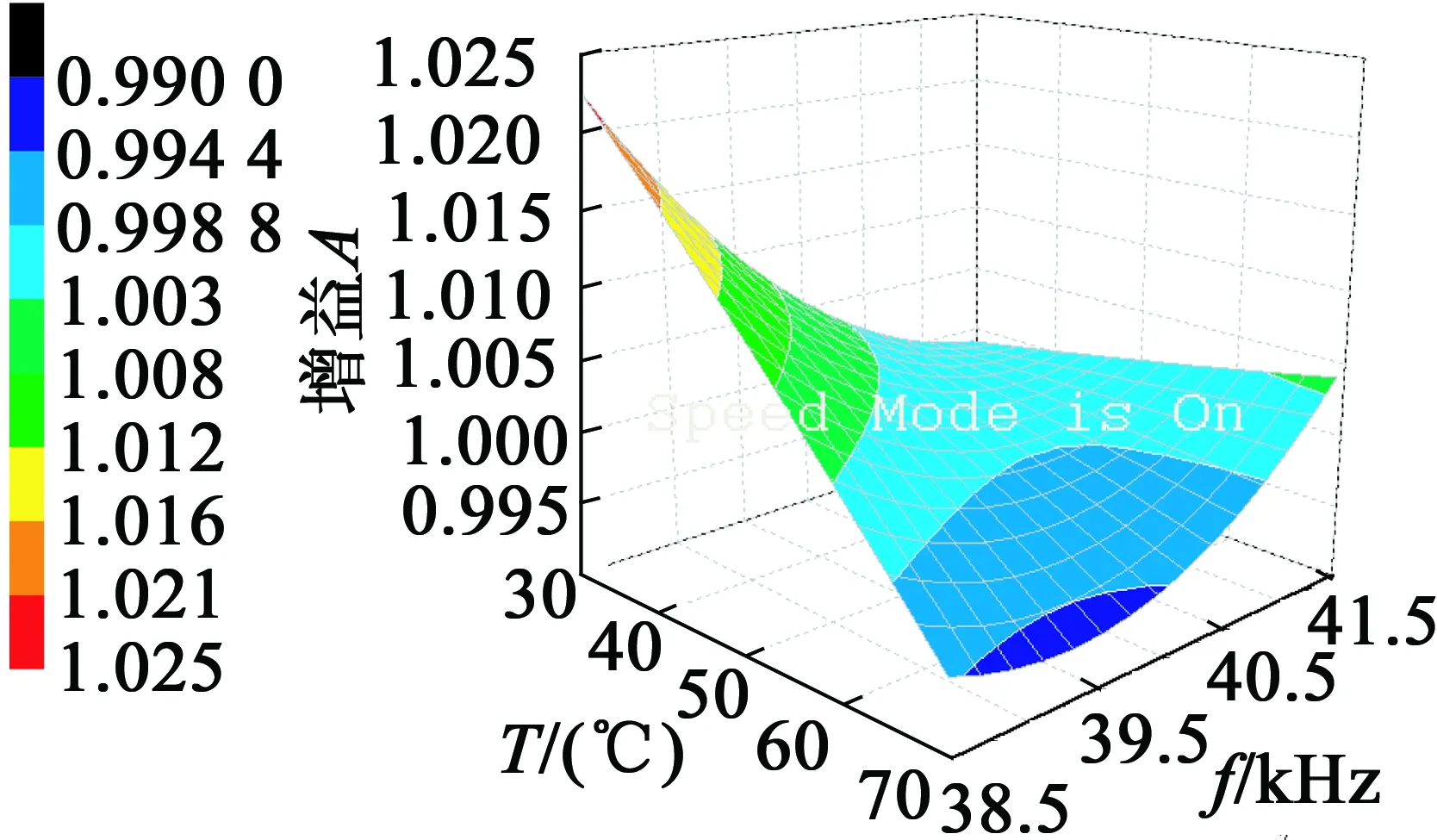
图9 LLCC匹配电路电压增益对温度

对比可知，LLCC匹配电路能较好地抑制温度和驱动电压频率对电压增益的影响，但电压增益最大值仅略大于1，几乎达不到升压作用。

3.3 匹配电路电压增益特性总结

根据以上计算和分析，对LC匹配电路、LCC匹配电路和LLCC匹配电路进行特性总结，如表1所示。虽然LLCC匹配电路电压增益基本不受温度和频率影响，但增益偏低。

表1 匹配电路电压增益特征总结

4 带反馈回路的LC匹配电路

本文把反馈的思想带入超声波电动机匹配电路，通过对输出采样，不断调节中间变量，从而使输出保持恒定，确保系统增益不受温度和驱动电压频率影响。另外，系统增益可通过改变输出目标值调节。

设计方案如图10所示，系统输入为互补的方波信号PWM_H和PWM_L，输出为电机端电压Vout。

图10 带反馈回路的LC匹配电路

主回路上由推挽逆变电路和LC匹配电路组成，实现电压增益。反馈回路由电压采样、PID控制器、PWM发生器和BUCK变换器组成。PID控制器根据输出电压采样值与电压目标值进行比对解算后，控制PWM发生器，产生一定占空比的PWM信号，从而控制开关管的通断。当开关管导通时，二极管VD反偏截止，漏极电流通过储能电感Lv向负载RL供电，Lv中的电流逐渐上升，电压Vcc上升，在Lv两端产生从左到右的自感电动势抗拒电流上升，将电能转化为磁能存储起来，滤波电容Cv是为了降低输出电压脉动而加入的；当开关管关断时，Lv两端产生从右到左的自感电势抗拒电流下降，使VD正向偏置而导通，于是Lv中的电流经VD构成回路，其电流下降，电压Vcc下降，Lv将存储的磁能转换为电能而释放出来给RL。

即依据输出驱动电压幅值，不断调整PWM占空比，控制变压器输入电压幅值Vcc，从而控制输出驱动电压幅值保持恒定。因此系统增益不受温度和驱动电压频率影响。

5 仿真实验

为验证本文的带反馈回路的LC匹配电路对稳定LC谐振电压增益的有效性，搭建对应仿真模型如图11所示，进行仿真研究。

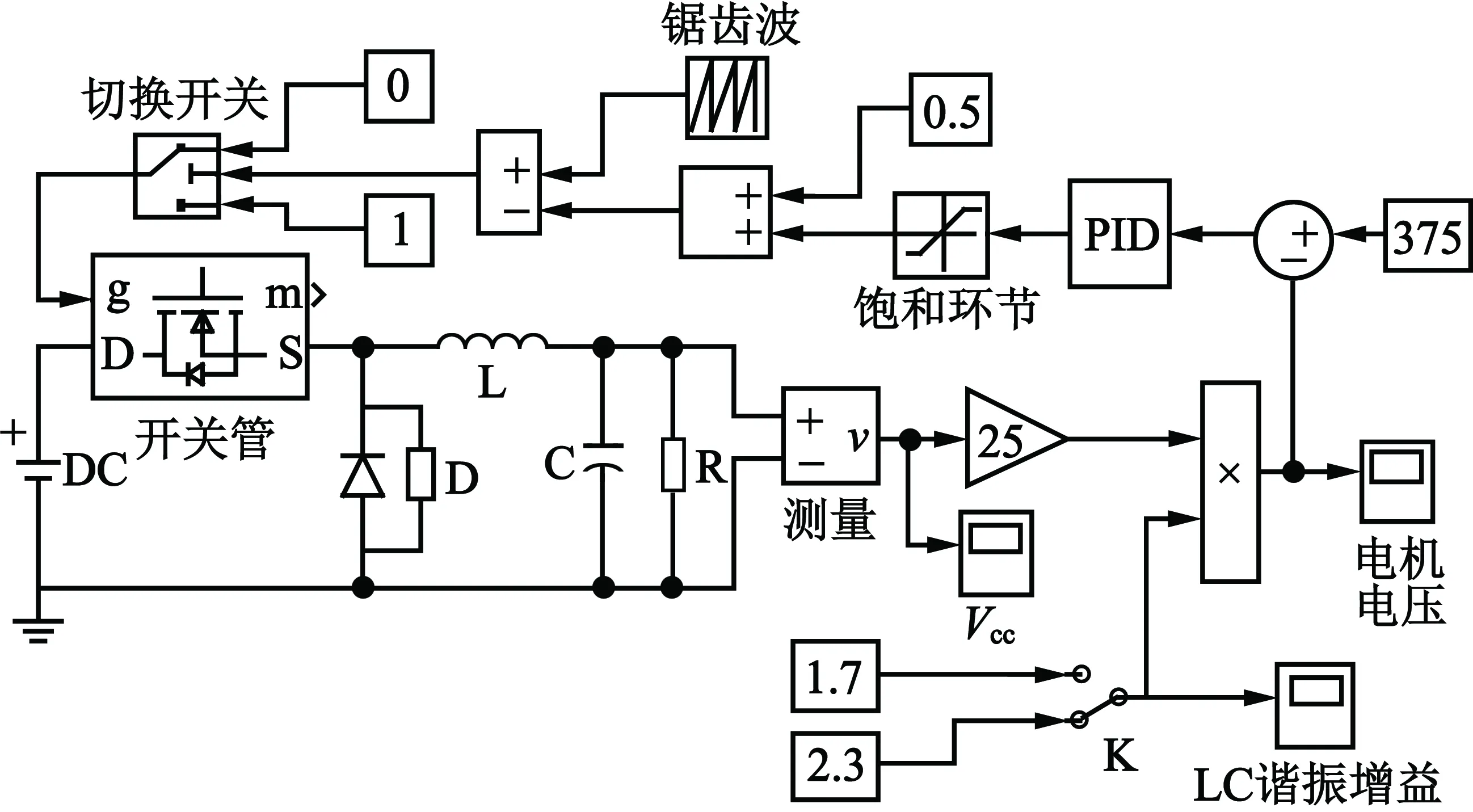
图11 带反馈回路的LC匹配电路仿真模型

以LC匹配为基础，由图5可知：在工作温度范围和稳定工作区频率范围内，其LC谐振增益变化范围为1.7～2.3；另外由于选用的超声波电动机在调频调速方式下的最佳驱动电压幅值为365～385 V，因此将输出电压目标值设定为375 V；输出电压幅值为直流电压值、占空比、变压器增益和等效LC谐振增益的乘积，由此选定占空比50%为基准，直流电压值为15 V，等效变压器增益为25；由BUCK电路参数整定方法确定R=100 Ω，L=1 mH，C=200 μF。

由此，在模型中，变压器与LC匹配电路分别简化为数值为25的定增益值和数值范围为1.7～2.3的变增益值；为保证输出电压幅值调整精度，PWM频率为100 kHz；PID参数分别为KP= 0.2，KI= 0，KD= 0；PID控制器输出系数的饱和上下限分别为+0.2和-0.2，即BUCK电路中开关管关断占空比调整范围为30%～70%。

当驱动电压频率由38.5 kHz变为41.5 kHz,且电机温度由30 ℃骤升至70 ℃时，LC谐振电压增益从1.7突变至2.3，系统调整过程如图12所示。

当系统中的LC谐振电压增益为1.7时达到稳态，Vcc=(8.82 ± 0.015) V，Vout=(374.7 ± 0.06) V ,稳态误差为0.3 V；当LC谐振电压增益突变为2.3时，Vout同时骤升至507.6 V，为此Vcc不断跌落，以使Vout降至目标值；经过6.18 ms，系统达到稳态，Vcc=(6.528 ± 0.009) V，Vout=(375.4 ± 0.06) V，稳态误差为0.4 V。可见，设计的闭环控制系统输出电压幅值基本保持恒定，且调节速度快、精度较高，即系统等效电压增益恒定。

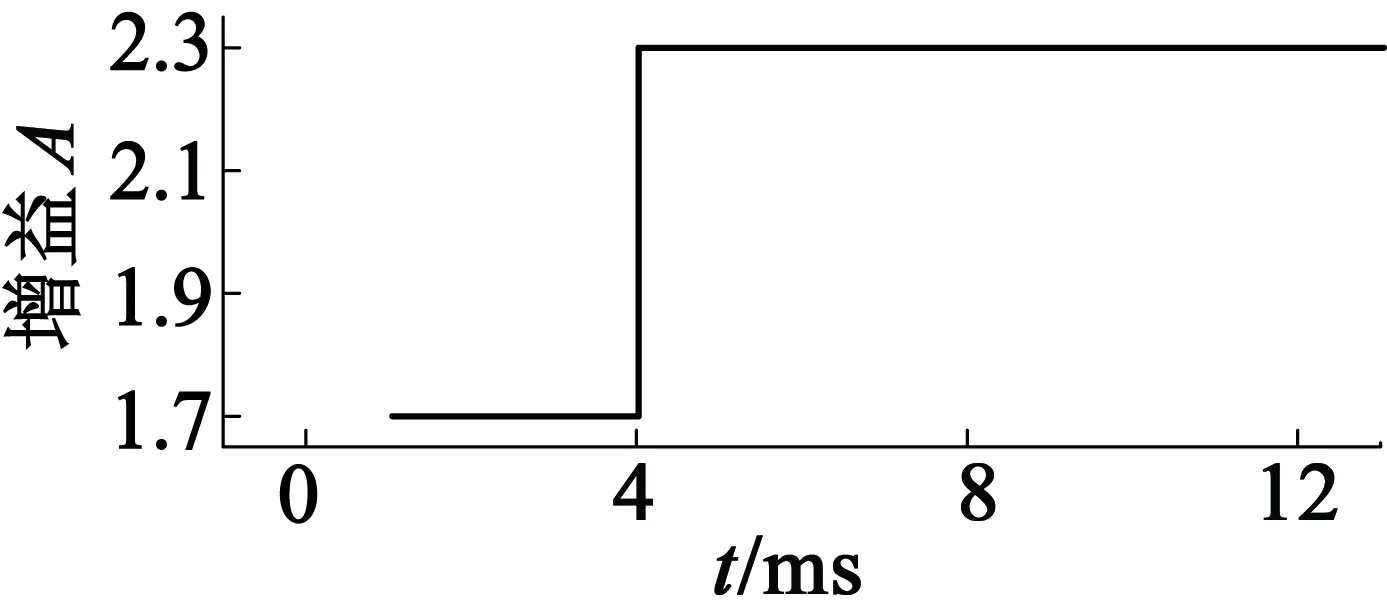
(a) LC谐振电压增益突变过程

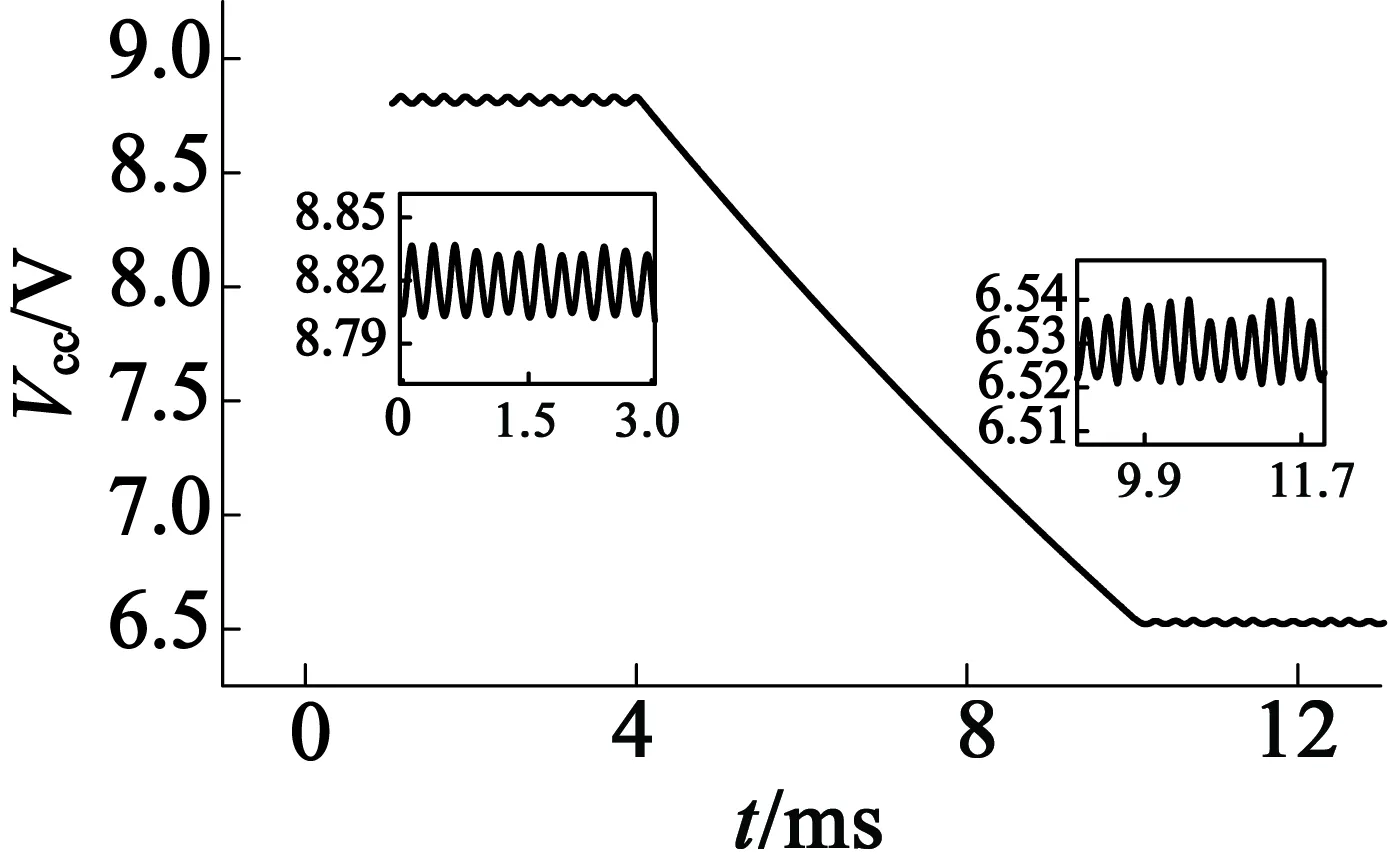
(b) BUCK电路输出电压Vcc

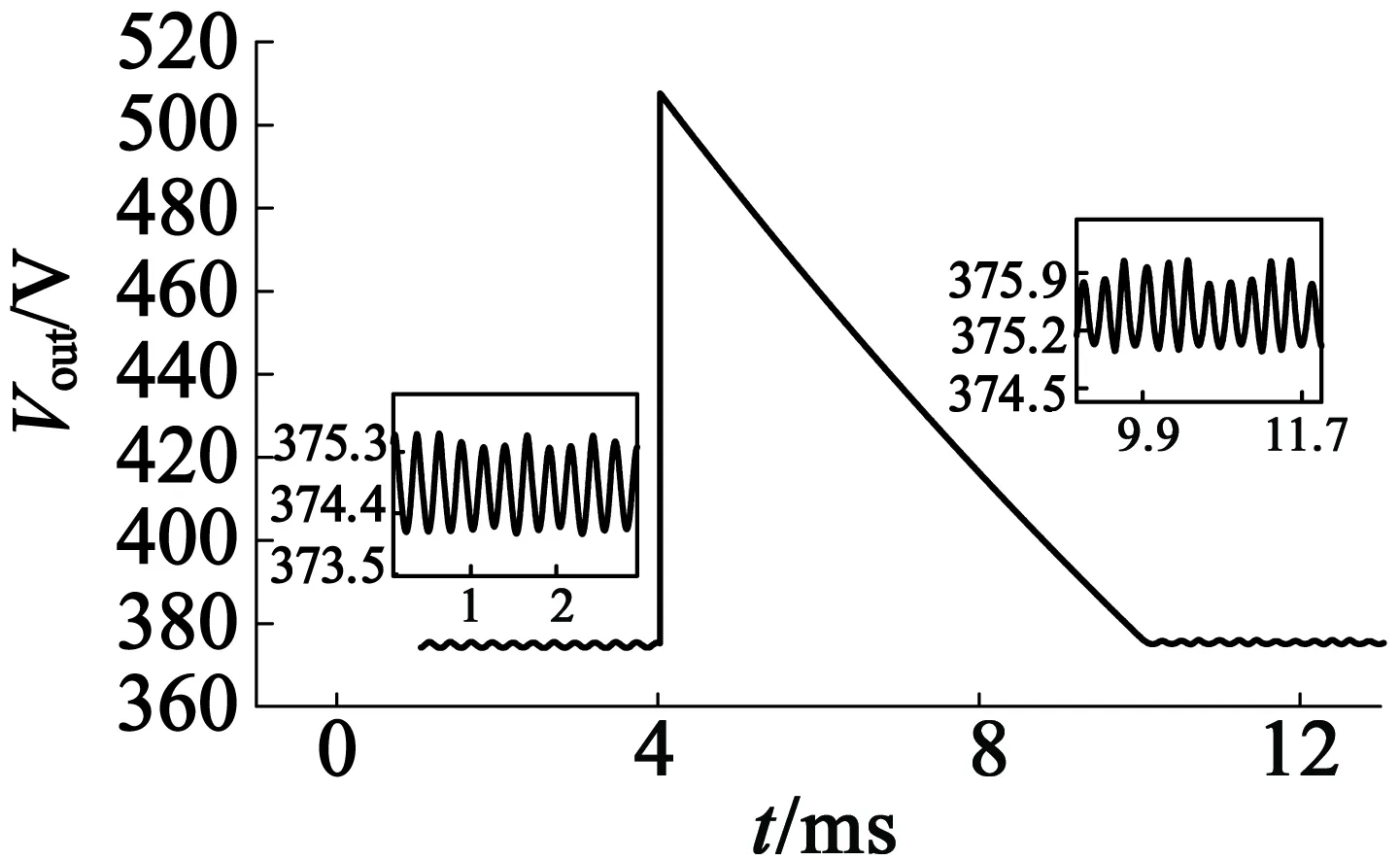
(c) 输出驱动电压幅值Vout调整过程

6 结 语

针对超声波电动机LC匹配电路的电压增益易受驱动信号频率和温度影响，从而造成调频调速方式下的电机转速控制变量耦合的问题，在对LC匹配电路、LCC匹配电路和LLCC匹配电路计算分析和总结的基础上，研究了一种带反馈回路的LC匹配电路，其调节速度快、精度较高，实现了超声波电动机转速控制变量解耦，且电压增益可调，显著降低了超声波电动机控制难度，对超声波电动机的推广与应用具有重要的意义。