考虑车辆续航里程的公交行车计划编制方法研究

陈定芳 （中南大学 交通运输工程学院，湖南 长沙 410075）

CHEN Dingfang (School of Traffic and Transportation Engineering,Central South University,Changsha 410075,China)

0 引言

编制每日行车计划是城市公交运营企业的核心业务，科学合理的行车计划不仅有利于更好地满足乘客需求，还有利于提高行车计划的执行率和调度效率，从而降低运营成本。常规公交行车计划包括发车时刻表、配车计划、排班计划三个部分。

传统编制常规公交行车计划主要采用顺次化的方法，三个部分生成步骤是一个顺序过程，目前针对这三个部分众多学者分别进行了深入研究：对于行车时刻表的研究大多是考虑公交运营成本和乘客满意度对发车间隔进行分析研究[1-2]；对于配车计划是以发车时刻表为基础，综合考虑公共交通企业的经济效益和乘客所得到的服务，协调制定车辆的车次链计划[3-4]；针对排班计划大多以班次最少和运营总成本最小为目标建立数学模型，利用列生成算法或启发式算法求解编制驾驶员排班计划[5]。也有学者针对行车计划一体化编制进行了研究，大多是假定单车场以及人、车数量相同，以客流需求为基础生成发车时刻表，然后利用基于准分配模型的竞拍算法或集合切割算法求解配车排班计划[6]。

以往在排班计划和配车计划编制的研究中是根据行车时刻表求解当日最优的人、车配置及人、车分配计划，并将发车时刻表独立考虑，忽略了行车计划编制过程中各部分之间的相关制约因素。然而，在公交线路营运中，由于浮动变化的客流需求、驾驶员固定的轮休规则及班型限制和车辆续航里程的限制，即使公交企业给公交线路配置好最优的人、车资源，也可能存在某天会出现人、车资源供给小于或大于需求的情况，人、车资源与需求难以每天均实现最优匹配，当人、车资源供给与需求没有达到最优匹配时该如何更合理地编制行车计划是一个实际有待研究与解决的问题。因此本文提出一种综合考虑车辆续行里程、驾驶员的各种班型共存、人车绑定关系等约束的公共交通行车计划一体化编制方法。

本文提出的公交行车计划一体化编制方法是在生成时刻表时综合考虑客流需求和线路现有的人、车资源约束，再将得到的行车时刻表作为营运基础同时考虑包乘制下人、车绑定关系集成调度生成排班计划和配车计划。

1 问题描述与建模

1.1 问题提出

本文研究的是在公交企业现有资源（人、车）约束要求下尽可能的满足客流需求生成行车时刻表，然后以行车时刻表为基础，以满足运营目标和人员、车辆有效工作时间最大化为宗旨，综合考虑驾驶员状态、车辆状态、人车线关系（包乘制）等约束条件，编制配车排班计划。该问题的约束条件有：

（1）每个车次有且仅有一位驾驶员和一辆车执行；

（2）每一位驾驶员和每一辆车同一时间只能执行一个车次工作；

（3）同一个驾驶员的两个连续车次之间发车时间间隔的限制；

（4）驾驶员的班制班型及对应的班型时段（发车时刻需在班型时段内）；

（5）包乘制下的人车关系限制；

（6）所有车都由车场驶至线路首末站开始营运，营运结束后需回到车场。

1.2 模型搭建

行车计划的编制可描述为营运任务（行车时刻表）的生成和分配任务（配车排班）两大部分。

1.2.1 行车时刻表编制模型

行车时刻表的编制实质是确定发车间隔。本文是以公交企业资源一定为约束，尽可能地满足客流需求为目标建立模型，用以确定各时段的发车间隔，是以最大化满足客流需求为目标，即客流需求与公交营运供给之间差值的绝对值最小为目标，如下所示：

式中：ti为i时段的发车间隔；Fmaxi为i时段最大断面小时客流量；C为车容量；ρi为i时段内的期望满载率。

同时需要满足以下约束条件：

（1）为保证公共交通企业的利益，线路时段的小时承载力不得大于线路时段的最大断面小时客流量，以免造成运力的浪费。

（2）每个发车时刻代表一次工作任务的起点，在此问题中所有生成的任务都需要被完成，故根据发车间隔计算出的i时段配车数不得大于i时段线路上班人数。

（3）线路营运任务总里程不得超出所有营运车辆的可营运续航里程总和，反之则有营运任务无法完成。

式中：L1,L2为上、下行营运里程；为i时段上、下行的营运任务数即营运车次数；m为线路时段数；lh为营运车辆h的可营运续航里程；a为所有营运车辆。

式中：hi为i时段的时段长度。

lh由营运车辆h自身的续航里程和其绑定驾驶员的班型共同决定。若车辆h自身的续航里程减去车辆从停车场到首末站的b个往返里程大于其绑定驾驶员的班型总估计最大车次数的总营运里程数（其中b为车辆h绑定的驾驶员人数），且车辆h的营运车次必须由其绑定驾驶员完成，则车辆h的可营运续航里程为其绑定驾驶员的班型总估计最大车次数的总营运里程数；反之，车辆h的可营运续航里程由其自身的续航里程所决定。具体关系如下：

式中：lzh为车辆h自身续航里程；l为车辆从停车场到首末站的1个往返里程；Dh为车辆h绑定驾驶员的班型总估计最大车次数的总营运里程数，每位驾驶员的班型估计最大车次数的总营运里程数由其班型时段和时段上、下行单程行程时长以及上、下行营运里程共同决定。

（4）时段发车间隔应不大于行政法规、标准规定的各地方各时段的最大发车间隔。

式中：tmaxi为i时段的法定最大发车间隔。

1.2.2 配车排班计划编制模型

本文是在行车时刻表的基础上，合理地生成驾驶员的班次链，再根据固定的人车关系生成所有的车次链。此问题中，营运任务一定且完成每一营运任务的成本固定，配车排班计划对营运成本影响不大但对驾驶员的有效工作时间比影响较大，因此本文将总的有效工作时间比最大化作为计划编制的目标：

式中：xjk为决策变量，表示驾驶员j是否选中营运车次k；tdk为营运车次k的单程行程时间长；Tj表示驾驶员j的在班时间，即为上班签到至下班签退的时段长度；K为所有营运车次；Q为所有营运驾驶员。

同时需要满足以下约束条件：

（1）确保每个营运车次k都能且仅能被一位驾驶员、一辆营运车辆所覆盖。

式中：yhk为决策变量，表示营运车辆h是否选中营运车次k；H为所有营运车辆。

（2）每位驾驶员选中的营运车次的总里程数，不得超过驾驶员对应车辆的总续航里程数。

式中：lh为营运车辆h的可营运续航里程数；Lk为营运车次k的营运里程数；H（）j为驾驶员j对应的所有车辆。

（3）每位驾驶员的班次链中的每相邻两车次之间的最小时间间隔约束，以保证每位驾驶员能够在其每一任务开始前到达任务开始地点。

式中：tfc、tfk为营运车次c、k的发车时间；tdk为营运车次k的单程行程时长；xjck为驾驶员j是否完成营运车次k之后又将开始营运车次c；tzk为营运车次k营运结束后的适当驻站时间。

（4）每位驾驶员的所承担的营运车次的发车时刻都应该在其班型时段内。

式中：tfk为营运车次k的发车时间；Tj1、Tj2为驾驶员j的上班时段的开始时间、结束时间。

（5）驾驶员j所承担的营运车次k都能且仅能被与驾驶员j有绑定人车关系的一辆营运车辆选中。

（6）定义决策变量为0-1整数变量，即表示不选中、选中。

2 求解算法

2.1 行车时刻表部分

本文中行车时刻表的编制是在资源一定的情况下尽可能的满足客流需求。在资源充足的情形下，各时段发车间隔是满足客流需求下的最大发车间隔；在资源缺乏的情形下，各时段发车间隔是资源充分使用下的最小发车间隔，可根据需要设定决策目标，本文以乘客总等待时间增加量最小为目标来采取策略调整发车间隔。具体计算步骤如下所示：

Step1：根据数学公式计算满足客流需求下各时段的最大发车间隔。

式中：tigmaxi为满足客流需求下时段i的最大发车间隔。

Step2：判断线路各时段营运驾驶员人数Pi是否大于等于各时段发车间隔为tjgmaxi时各时段所需要的最小营运驾驶员数Pmini，

其中：

（1） 若判断为是，则进入step3；

（2）若判断为否，则表示存在时段i的人车资源不能完全满足客流需求，同时需根据驾驶员资源调整时段i的发车间隔。将不能满足Pi≥Pmini的时段i的发车间隔重新计算，具体如下：

Step3：判断所有营运车辆的可营运续航里程总和是否大于等于各时段发车间隔为tjgmaxi时线路营运任务总里程。

（1）若判断为是，则发车间隔的计算完成，ti=tjgmaxi，并输出发车时刻表。

（2）若判断为否，则采取乘客总等待时间增加量最小为目标来采取策略调整部分时段i的发车间隔。具体调整步骤如下所示：

①计算需要减少的车次数nj。

②假设每个时段都减少nj，各时段的发车间隔将调整为同时判断是否存在tjgtzi≥tmaxi。若判断为是，令tjgtzi≤tmaxi对应的tjgtzi=tmaxi，其余tjgtzi=tjgtzi；若判断为否，令tjgtzi=tjgtzi。③计算（Fi为时段i的乘客人数），令最小的Ttzi对应的i时段的tjgmaxi=tjgtzi，其他时段i对应的tjgmaxi=jgmaxi，并重复step3，直至输出发车时刻表停止。

2.2 配车排班部分

配车、排班问题是一个非常复杂的组合优化问题，且被世界公认为NP难问题，通常采用列生成法和启发式算法求解。本文采用矩阵式编码遗传算法求解该问题，每一行代表一个营运车次，每一列代表一位驾驶员，如此可设定每一个营运车次和每一位驾驶员的相关属性更加简单便捷的添加约束条件，解决多种班型驾驶员共存的问题。目标函数作为适应度值。编码方式如下：

矩阵编码方法是将矩阵整体作为遗传子代个体，不需要将矩阵展开成一串元素，能确保子代个体基因的完整性。

若矩阵Ai为m×n阶矩阵，遗传子代第k代种群Pk个体的数目为｝表示该种群，其中：）称为矩阵染色体的基因元素

3 模拟计算与结果分析

实例数据说明：由客流需求、驾驶员班型及驾驶员绑定的车辆续行里程根据行车时刻表求解算法得到258个营运车次。其中驾驶员人数有31个，驾驶员班型有10个上午班、10个下午班和11个单班三种。

情形1：当驾驶员绑定的车辆续航里程无限大，即车辆的可营运续航里程为其绑定驾驶员的班型总估计最大车次数的总营运里程数时，以已生成的行车时刻表为基础，配车排班算法独立实验10次生成的满意解的最大值与最小值如图1、图2所示。

从图1、图2中可看出在10次独立实验中最后生成的满意解的适应度最大值与最小值的差值为0.00523，在此实例中每位驾驶员的平均在班时间约为8小时，可计算出这两次独立实验中平均每位驾驶员一天的空闲时间差值仅约为2.5min，31位驾驶员一天总的空闲时间相差77.8min，两次独立实验的差异很小。由此可见该算法的鲁棒性较好，结果稳定。

情形2：将此实例中的部分车辆续行里程进行限制，并且此部分车辆的可营运续航里程由其自身的续航里程所决定，但可以完成已生成的258个营运车次，此时算法运算结果的适应度值迭代情况如图3所示。

对比图1和图3可见其最大适应度值相差仅为0.0083，31位驾驶员一天总的空闲时间相差约123.5min，且适应度值有略微下降。这是因为当车辆续航里程受到限制但驾驶员、车辆资源能满足线路整天的营运要求时，与情形1比较这部分驾驶员的营运车次会减少，为保证线路营运高峰时段驾驶员的供给，这部分驾驶员需减少在非高峰时段的营运车次并在首末站做更长等待。

情形3：将部分车辆的续航里程进行限制且不能完成已生成的258个营运车次，本文讨论在完成同样营运车次下车辆续航里程对驾驶员有效工作时间比的影响，故在此对这一部分驾驶员做多绑定一辆车的处理以保证行车时刻表中营运任务的完成，并设定车场与线路首末站之间来回一趟约40min，此时算法运算结果的适应度值迭代情况如图4所示。

对比图1和图4可见其最大适应度值相差为0.0225，31位驾驶员一天总的空闲时间相差约334.8min，且适应度值有较大下降。这是因为本文中讨论的有效工作时间比是参与营运的时间与在班时间的比值，而驾驶员到车场进行换车的这一行为产生的车次为非营运车次，非营运时间的增加会降低驾驶员的有效工作时间比。

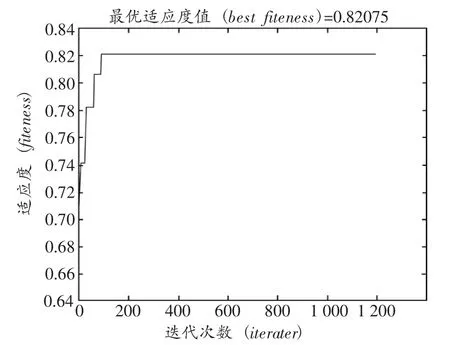
图1 不受车辆续航里程限制时满意解适应度最大值

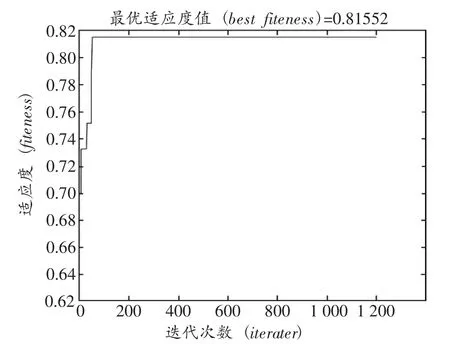
图2 不受车辆续航里程限制时满意解适应度最小值

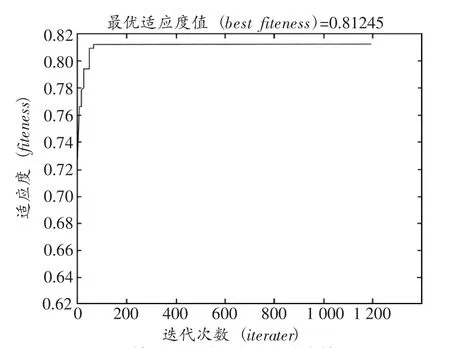
图3 情形2下的适应度值迭代情况

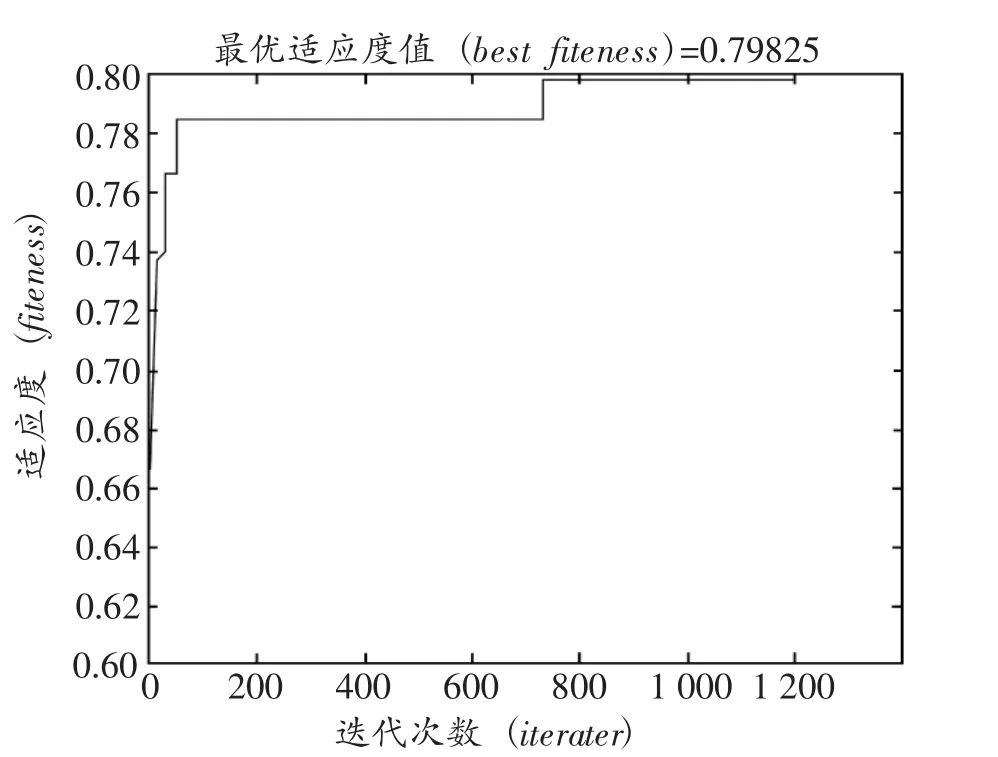
图4 情形3下的适应度值迭代情况

4 结论

本文提出了一种考虑车辆续行里程、驾驶员各种班型、人车绑定关系等约束将行车时刻表、配车计划、排班计划统一协调编制的常规公共交通行车计划一体化编制方法，并分别采用贪婪算法和矩阵编码式遗传算法有效地对行车时刻表、配车排班计划进行求解。能够有效地将公交线路现有资源与客流需求有机统一、协调分配，同时减少驾驶员的空闲休息时间，提高驾驶员有效工作时间比。通过实例对比分析发现车辆的续行里程对驾驶员的有效工作时间比有一定的影响，具体的影响方式和程度，以及考虑此种影响下如何更小营运成本的配置不同续行里程的车辆可进行进一步研究。