废塑料与兰炭混合燃烧动力学分析*
邢相栋 王 莎 张秋利 莫 川 陈云飞 宋英芳
0 引 言
兰炭结构为块状,粒度一般在3mm以上,颜色呈浅黑色。因其固定炭高、灰分低,逐步取代了冶金焦,在铁合金和碳化硅等产品生产中成为一种不可替代的炭素材料,可用于火法精炼粗铜以及用作含碳球团还原剂和高炉喷吹燃料等[1]。近年来,越来越多的塑料制品造成白色污染,引起了世界各国政府的广泛关注和环保科研工作者的极大重视,治理白色污染已刻不容缓。如何实现废塑料高效处理和回收利用得到广泛关注[2-4]。废塑料燃烧特性较好,具有良好的助燃效果,与兰炭混合燃烧能够符合高炉喷吹燃料用料要求。因此,将废塑料添加到兰炭中作为高炉喷吹燃料具有良好的应用前景。
目前,国内外对废塑料和兰炭混合燃烧的燃烧行为研究不够深入,而动力学研究作为燃烧反应过程的基础部分,可以用来深入探索废塑料和兰炭混合燃烧反应过程机理及其燃烧特性[5-8]。混合物燃烧有许多动力学研究方法,大部分为“无模型”或“模型拟合”[9]。在这种方法中,通过实验中的转换曲线估算动力学参数(活化能、指前因子和反应级数),假定某个反应级数,然后假设速率方程的微分或积分形式,对实验中的转化曲线进行线性回归获得直线图。这些方法有两个缺点:一方面,当只采用一种升温速率时,通过同一转换曲线可以得到不同的动力学参数值,得到的结果具有不确定性;另一方面,它通常只计算出一组动力学参数,没有考虑到复杂材料反应过程中的机制。随着计算机计算能力的提高,提出了一种复杂且准确的方法,该方法涉及多个升温速率,是一种非线性最小二乘法优化[10-11]。
本实验采用热重法分析废塑料和兰炭的混合燃烧,计算燃烧过程中的参数,探究混合物的燃烧机理,分析混合物燃烧过程中的动力学参数行为。分别采用体积模型(VM)、随机孔模型(RPM)和未反应核心模型(URCM)三种n阶反应气固模型,对三种模型的模拟结果进行分析,选择比较出最适合模拟废塑料和兰炭混合燃烧的模型,从而获得关于废塑料和兰炭混合燃烧机理,为废塑料和兰炭混合燃烧工业化应用提供理论参考。
1 实验部分
1.1 原料
实验所用的原料为兰炭粉(SC)和矿泉水瓶经处理过后的废塑料粉(WP)。矿泉水瓶的主要成分为聚对苯二甲酸乙二醇酯,为不含氯的无毒塑料。原料的工业分析和元素分析见表1。
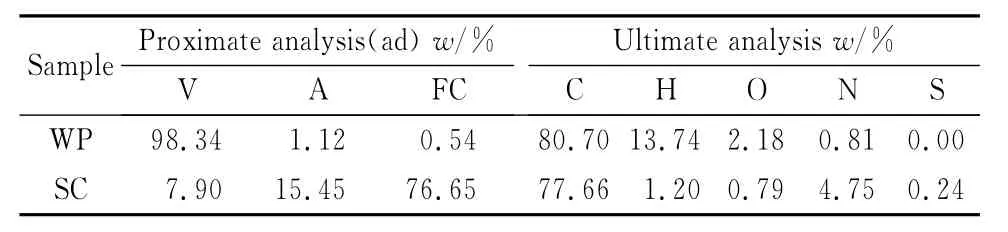
表1 废塑料及兰炭粉的元素分析和工业分析Table 1 Proximate and ultimate analysis of WP and SC
1.2热重实验
废塑料和兰炭混合物的燃烧采用热重法进行,热重分析使用STA449F3综合热分析仪(德国NETZSCH公司)。热分析仪的微量天平灵敏度小于±0.1mg,温度精度为±0.5K。废塑料粉分别以质量比0%,20%,40%,60%,80%和100%加入兰炭粉中。约5mg样品置于Φ5mm×2mm的刚玉坩埚中,坩埚置于TG支架上。实验以空气为燃烧气氛,分别以2.5K/min,5K/min,10K/min和20K/min的升温速率由环境温度升至1 173K,并记录样品的重量损失,实验数据由计算机自动采集。
通过式(1)计算混合物的燃烧率,也称为反应分数。

式中:m0为样品燃烧前的质量,g;mt为燃烧过程中某t时刻样品的质量,g;m∞为样品燃烧结束样品的质量,g。
1.3 动力学模型
假设废塑料和兰炭的混合燃烧是一种气固非催化非均相反应,燃烧速率可表示为式(2):

式中:k(T)为表观气化反应速率常数,取决于温度T,可以根据Arrhenius关系的温度函数表示。

式中:k0,E和R分别为指前因子,活化能和气体常数,T为绝对温度,K。
本实验采用体积模型(VM),随机孔模型(RPM)和未反应核心模型(URCM)三种n阶反应模型描述反应过程。
VM模型是最简单的模型,不考虑传热阻力和扩散阻力,也不考虑反应过程中样品的结构变化,假设反应在燃料颗粒上发生,反应过程中颗粒大小固定,燃料均匀地分布在颗粒的外部和内部;此外,VM模型假设反应表面积随着反应速率的增加而下降。燃烧速率可表示为:
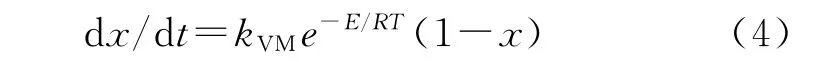
RPM模型广泛应用于碳质材料的气化或燃烧,该模型假设碳质材料含有孔,在反应期间孔表面随机重叠,同时考虑了燃烧初始阶段孔隙生长的影响以及由于相邻孔隙的聚结而导致的孔隙破坏,可以预测反应过程反应性的最大值。当燃烧过程受界面化学反应控制时,燃烧速率可写为:

式中:ψ是与初始样品的孔结构相关的参数。
当燃烧率x=0时,ψ的表达式为:

式中:S0,L0和ε0分别对应于初始孔表面积、孔长度和固体孔隙率。
SZEKELY et al[12]提出的 URCM 模型假设多孔粒子由均匀的无孔球形颗粒组成,并且反应最初发生在颗粒的外表面并且逐渐向内部移动,未反应核心随着反应的进行逐渐向内收缩。在反应过程中假设每一种颗粒均是未反应核心行为,随着反应的进行,仅剩下灰分。当通过界面处的化学反应控制燃烧过程时,燃烧速率描述如式(7):

MIURA et al[13]的研究结果表明,用一个升温速率确定的动力学参数可能会导致参数不可靠,如果仅用一个升温速率,则模型的拟合数据不能很好地验证模型,至少需要三个以上不同升温速率来估算可靠的参数和准确的活化能。因此,在本研究中,动力学参数由四个升温速率确定,分别以2.5K/min,5K/min,10K/min和20K/min的升温速率进行。
非等温热重方法或程序升温反应以恒定速率加热样品。温度T与时间t有关:

式中:β是升温速率,K/min。
将式(8)代入式(4)积分得:
目前,方程式(10)没有简单的解析解。之前的研究人员提出了许多近似解决方案,本实验选用了一个常见的解决方案[14](见式(12)):

这个近似值对于u>10是有效的,式(9)可以写成:
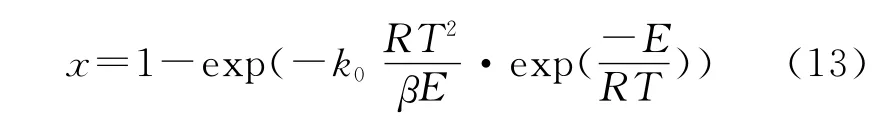
依此类推,式(5)和式(6)可以转化为式(14)和式(15):

通过比较实验和计算的x值,可以进一步测试和验证动力学模型。用式(16)计算实验曲线和计算曲线之间的偏差(xDEV):
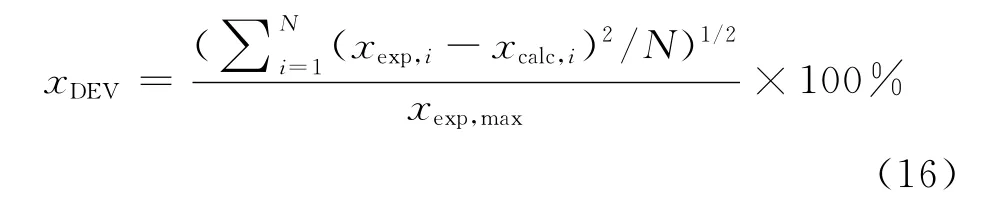
式中:xDEV为相对误差,%;xexp,i为实验数据;xcalc,i为模型计算值;xexp,max为实验曲线的最高值;N为实验的点数。
2 结果与讨论
2.1 热重曲线分析
在20K/min升温速率下,废塑料和兰炭混合物的燃烧率曲线和燃烧速率曲线见图1。
由图1可知,兰炭固定碳含量高,挥发分含量低,所以兰炭的燃烧率曲线只有一个明显的失重阶段,相应地,兰炭的燃烧速率曲线也只有一个明显的质量损失峰。废塑料自身不含水分或者水分含量很少,整个燃烧率曲线显示为多阶段。通过添加废塑料,混合物的燃烧过程可以大致分为三个阶段:第一阶段发生在室温到645K~650K之间,该阶段的质量损失主要为少量水分的蒸发,燃烧速率曲线峰值较小;温度继续升高到741K~763K,燃烧速率曲线的峰值高而尖锐,质量损失最大,此阶段主要是挥发分的析出;之后温度在793K~938K之间,该阶段为第三阶段,燃烧速率曲线的峰值低且宽,主要发生的反应为固定碳的燃烧。

图1 不同配比混合物的燃烧率和燃烧速率曲线Fig.1 Fractional conversion and burning rate curves of mixture at different blend ratio
混合物燃烧过程中的特征参数有:着火温度、燃尽温度,燃烧峰值温度及其对应的燃烧速率等。在DTG曲线上过峰值点A作垂线与TG曲线交于一点B,过B点作TG曲线的切线,该切线与失重开始时水平线的交点所对应的温度即为着火温度,记作Ti。燃尽温度为为混合物失重占总失重量98%时对应的温度,记作Tf。为了进一步研究废塑料对兰炭燃烧过程的影响,引入了燃烧特性指数S和点火指数C进行表征。
燃烧特性指数S定义为:

式中:Ti为着火温度;Tf为燃尽温度;Th为平均温度;Rmax为最大燃烧速率;Rmean为平均燃烧速率。
点火指数C定义为:

式中:S值越大表明燃烧特性越佳,C值越大表示煤粉的可燃性越好,燃烧越稳定。
燃烧过程中的参数如表2所示。由表2可知,废塑料的最大燃烧速率出现741.830K;对于兰炭的燃烧,最大燃烧速率出现在938.210K;而不同比例的混合物在不同温度下呈现出最大燃烧速率,废塑料配加量高的混合物最大燃烧速率出现的温度低于废塑料配加量低的混合物。随着废塑料配加量的增加,混合物的着火温度降低,而平均燃烧速率、点火指数C和燃烧特性指数S均增加。当废塑料配加量由0%增加到100%,C和S分别由1.39×10-8和6.49×10-14增加到5.37×10-8和5.68×10-13,表明通过废塑料添加可以改善兰炭的燃烧特性。

表2 20K/min升温速率混合物燃烧过程参数Table 2 Burning process parameters of mixtire at 20K/min heating rate
2.2 不同升温速率混合物的燃烧过程
当配加40%废塑料时,混合物在不同升温速率下的燃烧率曲线和燃烧速率曲线见图2。
由图2可知,不同升温速率下的燃烧率曲线和燃烧速率曲线彼此相似,随着升温速率的增大,燃烧率曲线、燃烧速率曲线和混合物的质量损失峰均向右偏移,这种现象称为热滞后现象[15]。出现热滞后现象主要有两个原因:一方面,随着升温速率的增加,温度上升更快,单个反应没有足够的时间完成,并且与相邻的高温反应重叠;另一方面,在较高升温速率下样品横截面的温度梯度增加,样品内外温差变大,表层燃烧产物来不及扩散,阻碍了内部可燃物燃烧,影响了热重仪器和样品之间的热传递。

图2 不同升温速率下配加40%废塑料混合物的燃烧率曲线和燃烧速率曲线Fig.2 Fractional conversion curve and burning rate curve of mixture with
由图2还可以看出,当升温速率由2.5K/min增加到20K/min时,混合物的Ti和Tf逐渐增加,其中Ti由456.15K增加到523.31K,Tf由848.17K增加到968.31K。Ti和Tf均升高,意味着燃烧性能的恶化,但是升温速率对燃烧过程的影响不能仅通过燃烧速率或Ti和Tf来判断。本实验还使用点火指数C和综合燃烧特性指数S来探究升温速率对混合物燃烧性能的影响,C和S均随着升温速率的增加而增加。当升温速率由2.5K/min增加到20K/min时,C由4.40×10-8增加到4.81×10-8,S由3.45×10-13增加到4.43×10-13。总之,可以确定,随着升温速率的增加,Ti,Tf,C和S均增加,对混合物燃烧速率具有明显的促进作用,因此,高升温速率可以改善样品的燃烧性能。

表3 配加40%废塑料混合物不同升温速率下燃烧过程参数Table 3 Burning process parameters at different heating rates with 40%waste plastic mixture
2.3 动力学分析
在不同升温速率下,基于前文提到的VM,RPM和URCM三种动力学模型,对废塑料和兰炭混合物燃烧进行分析,结果见图3。计算的动力学参数结果见表4。

表4 5K/min下三种模型下混合物的动力学参数Table 4 Kinetic parameters of mixture with three models at 5K/min
由图3可以看出,VM模型和RPM模型均可以较好地模拟废塑料和兰炭混合物的燃烧,而URCM模型模拟混合物的燃烧效果较差。由表4可知,RPM模型的R2值最高,这表明RPM模型拟合结果最好,当考虑孔重叠时,RPM模型预测燃烧过程中燃烧速率的最大值,在反应过程中,孔形状被假定为圆柱形,没有保持初始值,并且在反应发生时圆柱形径向生长。反应初始阶段,圆柱形逐渐生长导致总反应面积增加,这意味着更高的转化率,随着反应进行,相邻的孔隙重叠,反应结束时,由于孔隙重叠,总反应面积降低,因此反应速率降低。相反地,VM和URCM模型不能预测最大的反应速率,但是预测的反应速率是恒定降低的。
分析RPM模型计算出的动力学参数,可知混合物的活化能在17.86kJ/mol~89.14kJ/mol的范围内,随着WP配加量的增加,活化能先降低后增加,当废塑料配加量为80%时,获得的最低活化能为17.86kJ/mol,这种现象表明废塑料和兰炭混合物燃烧之间存在明显的协同效应。WANG et al[16]发现了类似的规律,在生物质和低阶煤的混燃过程中存在协同效应,在燃烧的第一阶段,挥发物含量的挥发和燃烧受到煤和生物质混合的限制。在燃烧的第二阶段,来自生物质的焦炭促进煤中固定碳的燃烧。由此可知,将生物质和低阶煤混合后,煤的存在限制了生物质中挥发分的挥发,而生物质灰中碱性物质的存在可明显促进煤中固定碳的燃烧。同时发现活化能(E)的增加伴随着指前因子(k0)的增加。活化能越低,相同温度下获得的活化分子越多,反应速度越快,反应速度同时也受指前因子的影响,指前因子表示活化分子的有效碰撞次数,指前因子越大,反应过程中有效碰撞的次数越多,因此反应速度越大。这种现象表明废塑料和兰炭混合物的燃烧存在“补偿效应”[17]。
为了量化三种动力学模型在预测燃烧率时产生的偏差,采用式(16)计算实验曲线和计算曲线之间的偏差(xDEV),计算结果见表5。
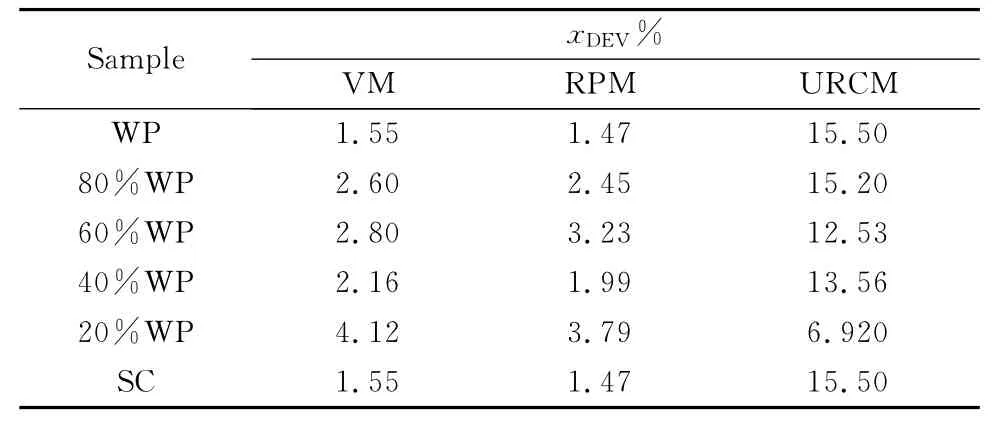
表5 实验曲线和计算曲线之间的偏差Table 5 Deviation between experimental curve and calculated curve
由表5可以看出,RPM模型计算的(DEV)是最小的,再一次验证,RPM模型是三种模型中模拟废塑料、兰炭混合物燃烧最好的模型。通过以上分析,可进一步为设计废塑料和兰炭混合燃烧的数学模型奠定基础。
3 结 论
1)废塑料和兰炭混合物燃烧分为三个阶段,分别为:少量水分蒸发、挥发分析出、固定碳燃烧。随着废塑料添加量的增加,点火指数C和燃烧特性指数S均增加,添加废塑料可以改善兰炭的燃烧特性。
2)升温速率越高,混合物的质量损失峰均向后偏移,出现热滞后现象,Ti,Tf,C和S 均增加,高升温速率对混合物燃烧速率具有明显的促进作用。
3)RPM模型比VM模型和URCM模型更好地描述了废塑料和兰炭混合物的燃烧,使用RPM模型计算混合物的活化能,活化能在17.86kJ/mol~89.14kJ/mol的范围内,随着废塑料添加量的增加,活化能先降低后升高,当废塑料添加量为80%时,得到最低的活化能为17.86kJ/mol。
符号说明
x——混合物的燃烧率,无量纲
m0——样品燃烧前的质量,g
mt——燃烧过程中t时刻样品的质量,g
m∞——样品燃烧结束样品的质量,g
dx/dt——混合物的燃烧率,s-1
k(T)——表观气化反应速率常数,取决于温度(T)
f(x)——反应分数的函数
k0——指前因子,无量纲
E——活化能,kJ/mol
R——气体常数,8.314J/(mol·K)
T——绝对温度,K
kVM——模型VM的指前因子,无量纲
kRPM——模型RPM的指前因子,无量纲
ψ——与初始样品的孔结构相关的参数
S0——初始孔表面积,m2/g
S——燃烧特性指数
C——点火指数
Ti——着火温度,K
Th——燃尽温度,K
Rmax——最大燃烧速率,s-1
Rmean——平均燃烧速率,s-1
T1——最高燃烧速率对应的燃烧温度,K
T2——第二高燃烧速率对应的燃烧温度,K
Tmeam——平均温度,K
Rmax-1——T1的燃烧速率,s-1
Rmax-2——T2的燃烧速率,s-1
L0——初始孔长度,nm
ε0——初始孔的固体孔隙率,%
T0——初始温度,K
B——加热速率,K/min
DEV——相对误差,无量纲
xexp,I——实验数据,无量纲
xcalc,I——模型计算值,无量纲
max(x)exp——实验曲线的最高值,无量纲
N——实验的点数,个

