类比思想巧解大学物理问题

樊炎曦 赵岚月 叶雅婧 叶晴莹,2

(1. 福建师范大学物理与能源学院;福建 福州 350117； 2. 福建省量子调控与新能源材料重点实验室，福建 福州 350117)

高中物理的学习中,方法很重要,这些方法可能就隐藏在各个学科之中,需要我们善于发现并加以利用. 运用类比推理法能很好地解决某些物理解题.这些难题可能超出所学知识范围,但所运用的思想方法并不陌生.笔者将根据高中所学知识，运用类比推理的方法解答一道大学物理中变力做功问题,例题如下.

图1

例1.如图1,在动摩擦因数为μ的桌面上放置一根柔软的链条,长度为L,将链条推出,使其垂直悬挂部分长度为a并由静止开始下落,求链条恰好离开桌面时的速度.

此题难点在于链条所受的摩擦力和重力分别由于链条与桌面间的正压力和竖直端链条质量随着链条下降的高度变化而变化. 假设链条单位长度质量为λ.

若运用大学物理知识,解法如下.

如图1建立坐标系,假设链条垂下部分长度为x.链条所受重力为G=λgx.(x为竖直垂下部分链条长度)链条所受滑动摩擦力:f=μλg(L-x).由牛顿第二定律有

F=G-f=λgx-μλg(L-x)=ma，

(1)

其中

(2)

联立(1)(2)式得

[λgx-μλg(L-x)]dx=λLvdv.

两边同时积分

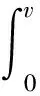
解得

这种方法需要用到高等数学微积分的方法. 我们也可以根据高中物理所学知识试分析一下.

由(1)式可知链条所受的合力并非恒力. 将系统所做的功分为重力功WG与摩擦力做功Wf. 重力为保守力,做功只与竖直悬挂链条始末状态有关,则不难求解.

考虑到链条所受摩擦力:

f=μλg(L-x)=μλgL-μλgx=f1+f2，

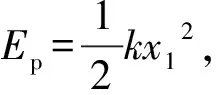
解法如下.

如图1:对于重力做功,只需考虑竖直链条始末状态. 以桌面所在水平面为零势能面,则链条初始状态重力势能:

(3)

末状态重力势能:

(4)

联立(3)(4)式可得

WG=-ΔEp=(Ep1-Ep0)=

(5)

链条受到的摩擦力:

f=μλgL-μλgx=f1+f2.

对于恒力f1有:

Wf1=f1Δx=μλgL(L-a).

(6)

对于变力f2,类比于弹性力:

f2=-μλgx=-kx，其中k=μλg.

其初始位置具有的“势能”:

末位置具有的“势能”:

则

Wf2=-ΔEp=-(Ep1-Ep0)=

(7)

联立(6)(7)式可得此过程摩擦力做功为

Wf=Wf1+Wf2=μλgL(L-a)-

(8)

联立(5)(8) 式,由动能定理:

得

此类变力做功的问题,虽在高中物理课程中并未涉及,但我们根据类比方法,可以解决此类变力做功的问题.