一种自适应滑模临近空间飞行器跟踪制导方法*

刘开封，孟海东，陈奇昌，陈 颖，王长江

(火箭军研究院第六研究所，北京 100090)

0 引言

标准弹道/轨迹制导法(也称跟踪制导法)是在航天飞行器工程领域中得到成功应用的制导方法[1]。由于临近空间的环境复杂性和不确定性，处于临近空间飞行的飞行器实际飞行轨迹可能与参考轨迹存在较大偏差，普通的基于状态方程线性化的跟踪制导方法对于小扰动情况效果较好，但应用于如临近空间之类大扰动跟踪制导时，状态方程线性化可能造成较大的制导方法误差[2]。因此，文中设计了一种具有积分型切换函数的自适应滑模制导方法(adaptive sliding mode guidance with integral switch function, ISFASMG)，该方法基于线性二次型调节器(linear quadratic regulator, LQR)设计反馈增益，并在LQR跟踪制导律表达式中增加了自适应制导项，修正线性化跟踪制导的方法误差，使其具有更强的鲁棒性，适用于大扰动的临近空间跟踪制导。

1 基于ISFASMG的纵向跟踪制导方法

1.1 具有积分型切换函数的滑模控制

考虑如下线性不确定系统:

[B(t)+ΔB(t)]U(t)+[D(t)+ΔD(t)]TL

(1)

式中:ΔA、ΔB和ΔD分别为系统参数和外加干扰的不确定性；TL为外加干扰。

上述系统可转换为:

(2)

式中:E(t)为总不确定项，具体如下:

(3)

式中:B+=(BTB)-1BT。

设计如下积分型切换函数:

(4)

式中:F为正常数矩阵；K为状态反馈增益矩阵。

(5)

由上式可以看出，通过设计状态反馈增益K，可达到理想的控制效果。

设计控制器为[3]:

(6)

由式(4)对t求导，并将式(2)和式(6)代入，得:

Bf·sgn[s(t)]+BE}

(7)

FB{E-f·sgn[s(t)]}

(8)

则:

FB[E·s-f·abs(s)]

(9)

由于f≥abs[Ei(t)]，则:

(10)

说明系统稳定。

由式(6)可以看出，滑模控制器在线性反馈的基础上增加了一项f·sgn[s(t)]，而f≥abs[Ei(t)]。又由式(3)可以看出，Ei(t)反应了系统参数误差和外部干扰，因此滑模控制器可修正状态方程线性化的方法误差和外部干扰，具有更强的鲁棒性。

1.2 自适应控制器设计

由式(6)可以看出，控制器中需要确定E(t)的上界。然而，在实际控制过程中，总不确定项E(t)的上界往往难以确定，因此需采用自适应控制方法，实现对E(t)的上界的自动自适应估计。

(11)

式中:ε为自适应项的增益向量，满足ε>0。

则自适应滑模控制律设计为:

(12)

定义Lyapunov函数:

(13)

则:

(14)

由式(11)，同式(9)推导，得:

(15)

(16)

由式(15)和式(16)，则式(14)可转换为:

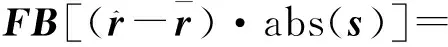
(17)

即证明了自适应滑模控制的稳定性。

1.3 基于LQR的状态反馈增益设计

基于积分型切换函数的滑模控制需要合理的设计状态反馈增益矩阵K，文中基于线性二次型调节理论[4]设计反馈增益。

线性系统描述如下：

(18)

式中:X(t)为系统状态；U(t)为控制变量；Y(t)为系统输出。

如果希望系统的理想输出为Y*(t)，则e=Y*(t)-Y(t)为误差向量。

对于终端时间自由的最优控制问题，通常定义以下形式二次型性能指标:

UT(t)T(t)U(t)]dt

(19)

式中:Q(t)为对称半正定矩阵；T(t)为对称正定矩阵；积分式中eT(t)Q(t)e(t)和UT(t)T(t)U(t)分别为状态误差和控制误差，积分表示过程误差的累积。

当C(t)=I，理想输出Y*(t)=0时，则控制的目的是使Y(t)=X(t)=e(t)=0。即用最小的控制量使状态保持在零值附近，称为线性二次型状态调节问题。

根据Hamilton极小值原理，得上述系统的最优控制为：

U*(t)=-T-1(t)BT(t)P(t)X

(20)

P满足如下Riccati微分方程及边界条件:

(21)

令最优增益矩阵K为：

K=-T-1(t)BT(t)P(t)

(22)

则：

U=KX

(23)

1.4 纵向跟踪制导问题建模

假设地球为不旋转均质圆球，得纵向运动方程为[5-6]：

(24)

由上式可以看出，纵向运动仅与倾侧角大小相关，因此可通过调节攻角和倾侧角大小跟踪纵向轨迹，而通过倾侧角符号控制航向实现侧向轨迹的跟踪。

(25)

式中：

式中:CLv、CLr、CLα为气动升力系数CL对v、r、α的偏导数；CDv、CDr、CDα为气动阻力系数CD对v、r、α的偏导数；ρr为大气密度ρ对地心矢径r的偏导数。

为简化计算，可令二次型性能指标中加权矩阵Q和T为对角矩阵，则二次型性能指标可转换为:

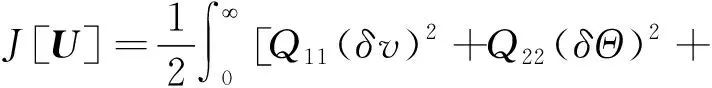
Q33(δr)2+T11(δα)2+T22(δ|γc|)2]dt

(26)

式中:Q11、Q22和Q33分别为矩阵Q的对角线元素，T11和T22分别为T的对角线元素。为反映各参数之间的权重比，参照文献[7-8]，可令：

其中δvmax、δΘmax、δrmax、δαmax和δ|γc|max分别为对v、Θ、r、α和|γc|的跟踪误差最大允许偏差，需根据经验或仿真结果人为设定。

至此，根据式(21)和式(22)，便可计算出LQR反馈增益矩阵K。

(27)

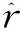
将式(4)变形得:

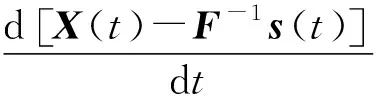
(28)

(29)

由式(27)可以看出，基于积分型切换函数的自适应滑模制导方法较普通LQR跟踪方法，增加了一项自适应项，该项反映了对系统参数和外部干扰不确定性的自适应修正，包括大扰动情况下状态偏差线性化带来的方法误差，增加了制导系统的鲁棒性。

2 基于航向走廊的侧向制导方法

纵向跟踪控制器仅能确定倾侧角γc的大小，不能确定它的符号。因此必须实施侧向制导以确定倾侧角γc的符号，从而获得完整的制导指令。

通常通过定义航向角偏差走廊实现对侧向轨迹的控制。航向角偏差走廊定义为：以单调变量为自变量(通常为速度v或待飞航程Stogo)，航向角偏差ΔΦ的允许范围构成的走廊形区域。当飞行器位于航向角误差走廊中时，代表侧向轨迹在允许偏差范围内，应保持当前倾侧角符号不变；当飞行器超出航向角偏差走廊时，继续保持当前倾侧角符号会导致航向角偏差增大，并越来越超出偏差走廊，此时应改变倾侧角符号，即翻转再入体，使航向角误差减小并使轨迹回到航向角偏差走廊中。

通常[9-10]，航向角偏差走廊设计为“漏斗形”的形状，如图1所示。为提供良好的初始条件，航向角偏差走廊在初始阶段应取较小的允许范围；在中间部分，为避免倾侧角频繁改变符号，导致再入体频繁翻转增加控制系统负担，中间部分取较大的允许范围；在终点时，为保证到达终点的精度，偏差走廊也应取较小的允许范围。

图1 航向角偏差走廊示意图

3 仿真结果及分析

设置初始偏差为：δv=100 m/s、δΘ=1°、δΨ=1°、δr=200 m、δλ=0.1°、δφ=0.1°。纵向最大允许偏差为：δvmax=10m/s、δΘmax=0.05°、δrmax=200 m、δαmax=0.2°、δγcmax=1°。气动系数误差服从均值为0的正态分布，标准差为气动系数值的5%，自适应系数取ε=[5,1,3]T。

分别采用LQR跟踪制导和ISFASMG跟踪参考轨迹，单次仿真结果对比如图2～图10所示。由仿真结果可以看出，使用ISFASMG方法，速度、当地速度倾角和地心距离初始误差能够很快的减小到一定范围，说明文中的反馈增益设计和自适应滑模制导设计合理；中期跟踪轨迹与参考轨迹存在一定的偏差，是由于中期设置了较大的航向角偏差容许值，但在末段由于航向角偏差容许值减小，跟踪轨迹基本与参考轨迹重合；在中期倾侧角仅翻转了一次，在接近终点时为精确控制航向，倾侧角翻转了3次，总翻转次数较少，说明航向误差走廊设计合理。

并且，ISFASMG对纵向轨迹参数的跟踪精度明显优于LQR，由于文中考虑5%的气动参数误差，在再入末期，气动参数值较大，对应气动参数误差也较大时，LQR跟踪制导方法对高度与速度跟踪误差较大，导致跟踪轨迹与参考轨迹偏差较大，而ISFASMG仍能够实现稳定的跟踪，证明了ISFASMG在大参数偏差下的鲁棒性优势。

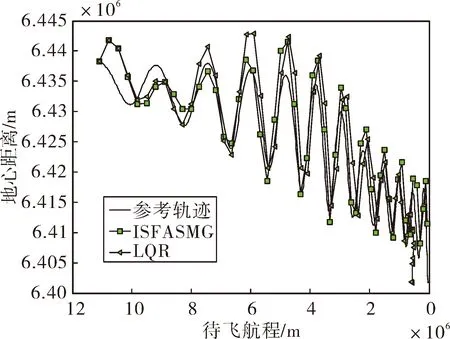
图2 地心距离跟踪对比

图3 速度跟踪对比

图4 当地速度倾角跟踪对比

图5 航向角控制对比

如图11所示，100次跟踪轨迹打靶结果表明，ISFASMG方法能够始终将终点参数偏差控制在合理的范围，经统计ISFASMG制导精度偏差(圆概率偏差，circular error probable, CEP)约为LQR的1/12左右。

图6 指令攻角与参考攻角

图7 指令倾侧角与参考倾侧角

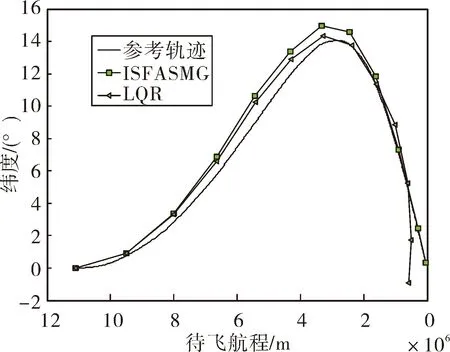
图8 纬度变化对比

图9 经度变化对比

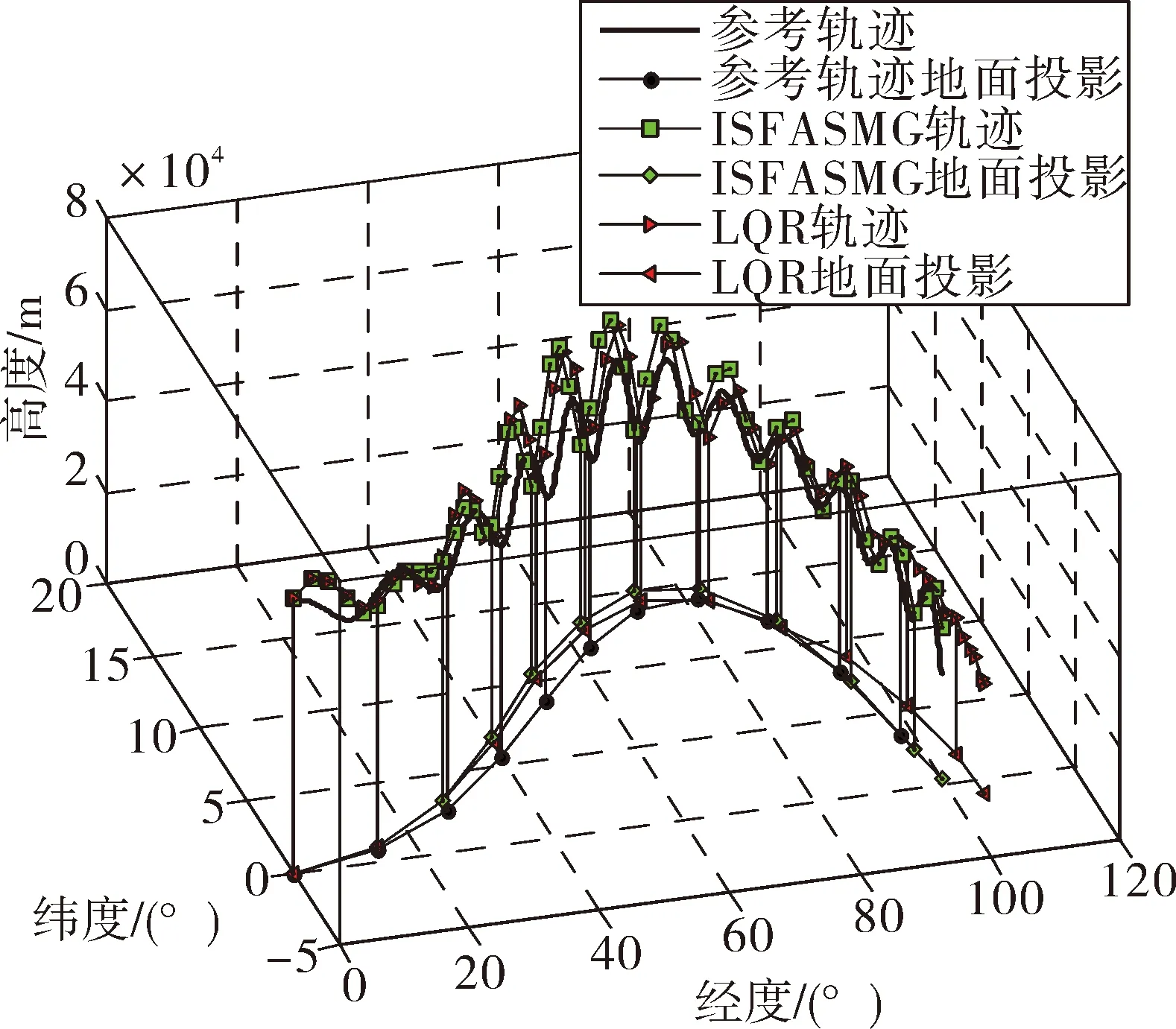
图10 三维轨迹变化对比

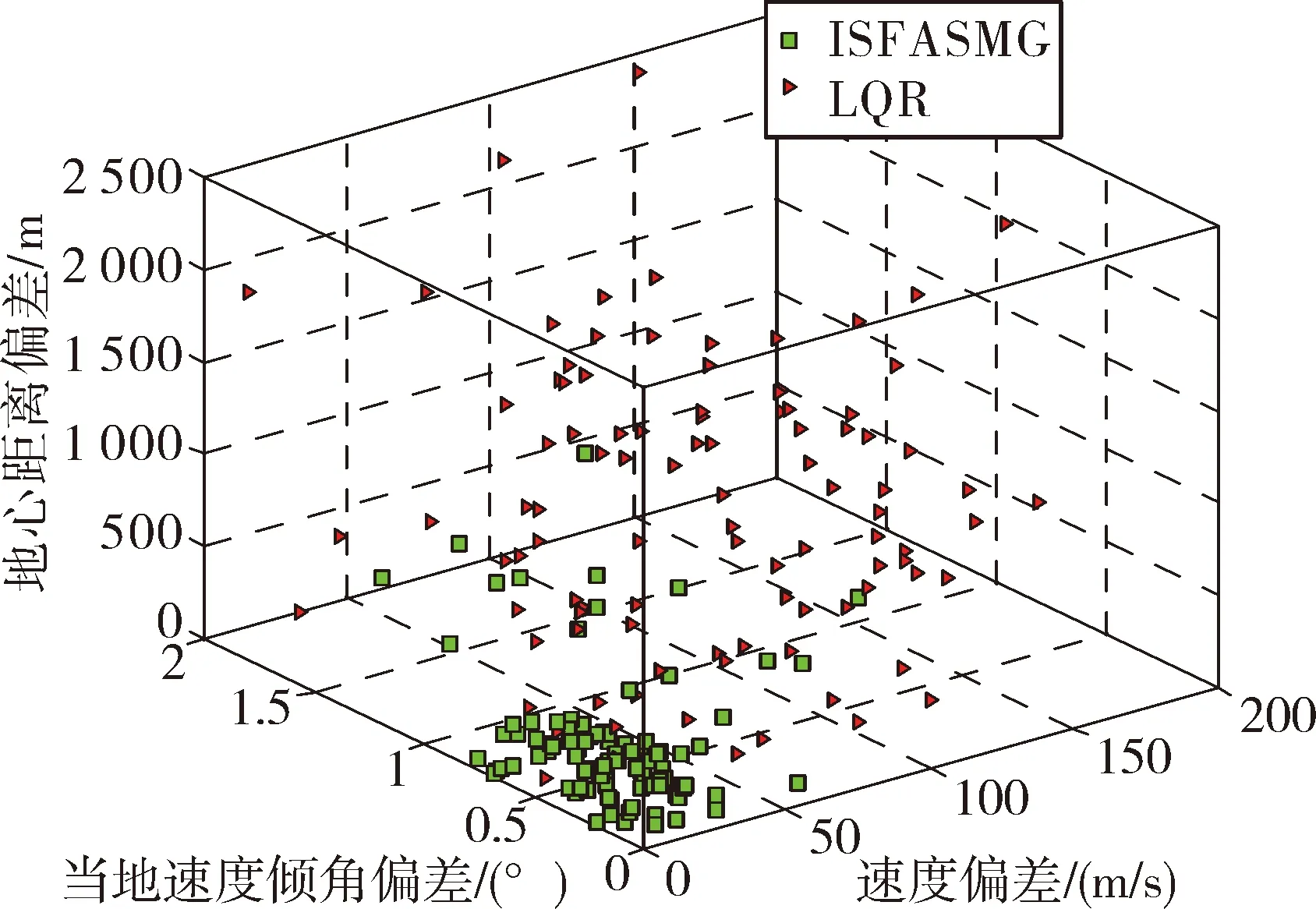
图11 终点状态偏差统计

4 结论

文中设计了一种具有积分型切换函数的自适应滑模制导方法，该方法在LQR跟踪制导律中增加了自适应项，修正了状态方程线性化的方法误差和外部干扰，使其具有更强的鲁棒性，适用于大扰动的临近空间飞行段制导。对比仿真结果表明，ISFASMG方法能够很好地对纵向轨迹参数进行跟踪，大扰动情况下制导精度明显优于LQR跟踪制导。