制动缸用星形密封圈的优化设计
鲍春光 韩红文 朱君华
(中车戚墅堰机车车辆工艺研究所有限公司 江苏 常州 213011)
星形密封圈又称X形密封圈,是有4个密封唇的圆环状橡胶密封圈,可起双向密封作用,在使用上与O形圈工作原理类似,但较O形圈具有更多优点。星形密封圈在往复运动时不会在沟槽内扭曲滚动,比O形圈所需的径向应力小,摩擦力小且寿命长。星形密封圈截面上压力分布均匀,密封效果更佳;由于模具分型面设在2个唇之间,因此飞边不会影响密封效果;在密封唇之间形成的润滑容腔,改善了启动状况[1]。星形密封圈在动态或静态场合密封气体、液体中均应用,适合于往复运动的活塞、活塞杆、柱塞,也能在摆动、螺旋和旋转状况下适用于轴和心轴等。文中介绍了一种应用于停放制动缸中间体径向内周往复动密封的星形密封圈设计应用情况。
1 星形密封圈几何模型设计
结合制动缸密封系统实际结构,建立星形密封圈/中间体沟槽和制动力推套组成的二维轴对称几何模型(见图1)。星形密封圈的截面形状是按照四角对称布置的圆形唇边与两唇间凹陷相切的过渡圆弧边组合成封闭的截面。根据制动力推套与星形密封圈的配合直径105 mm,查阅相关标准及选型手册,确定星形密封圈的截面长度为3.5~5.5 mm,密封圈唇边圆弧和过渡圆弧上下限尺寸与截面长度内在关联;参照O形圈气动动密封压缩率5%~20%,结合截面长度确定密封圈的初始预压缩量;安装状态制动力推套和中间体沟槽间单边间隙取值0.2 mm,间隙处沟槽圆角半径取值0.2 mm;沟槽深度根据星形密封圈初始截面长度、安装过程的预压缩量和装配间隙来确定,沟槽宽度取值6 mm。由于星形密封圈截面长度、圆弧半径尺寸以及压缩率均在一定的范围区间,需要通过设计校核来确定优化方案值以便完成密封系统最终几何尺寸定型,文中通过有限元仿真分析结合正交试验方案设计的方法,以获得能达到最好动、静密封性能的密封圈截面尺寸和预压缩量。

图1 密封结构几何模型
2 星形密封圈仿真分析
2.1 仿真初始几何参数
用于初始仿真的密封圈参数值确定如下,截面长度值4.8 mm,唇边圆弧半径0.6 mm,过渡圆弧半径2 mm,压缩率取10%来确定预压缩量为0.48 mm,密封圈与中间体沟槽和制动力推套的接触摩擦系数取0.2。
2.2 材料特性
中间体沟槽和制动力推套的取材为中碳调质钢,弹性模量E=2.06 GPa,泊松比ν=0.3,密度ρ=7 800 kg/m3。
星形密封圈采用丁腈橡胶,属于超弹性体,具有材料非线性、几何非线性和接触非线性。本文选用Mooney-Revlin模型来描述其力学特性,其应变能函数可表示为:
W=C10(I1-3)+C01(I2-3)
(1)
式中:W为应变能密度;C10、C01为橡胶材料Mooney-Revlin模型系数,本文C10、C01的取值分别为1.87和0.47;I1、I2分别为第一、第二应变张量不变量[2]。
其中应力与应变之间的关系为:
σ=∂W/∂ε
(2)
应力表征为应变能函数对应变的偏导数,式中σ为奥雷-克希霍夫应力;W为单位体积的应变能函数;ε为格林应变张量的分量。
2.3 边界及载荷条件
从静密封、动密封两种工况来分析研究密封圈的力学性能。静密封加载过程分为两步:(1)完成初始预压缩,对制动力推套施加径向位移0.48 mm;(2)对密封圈与气流接触一侧施加1.2 MPa工作压力,实现静密封。在静密封基础上,对制动力推套施加轴向速度载荷完成动密封,运动方向与气流方向相反。
2.4 评价标准
通过密封圈 VonMises 应力及主密封面上的接触应力分布情况,来判断密封圈设计优劣。VonMises 应力是基于剪切应变能的一种等效应力,用来对密封圈的破损失效和疲劳失效进行评价,其值越大,密封圈发生破坏的几率越大[3]。密封圈与其他物体主要起密封作用的接触面上的接触应力大于工作气压时,可实现良好的密封。
2.5 初步分析结果
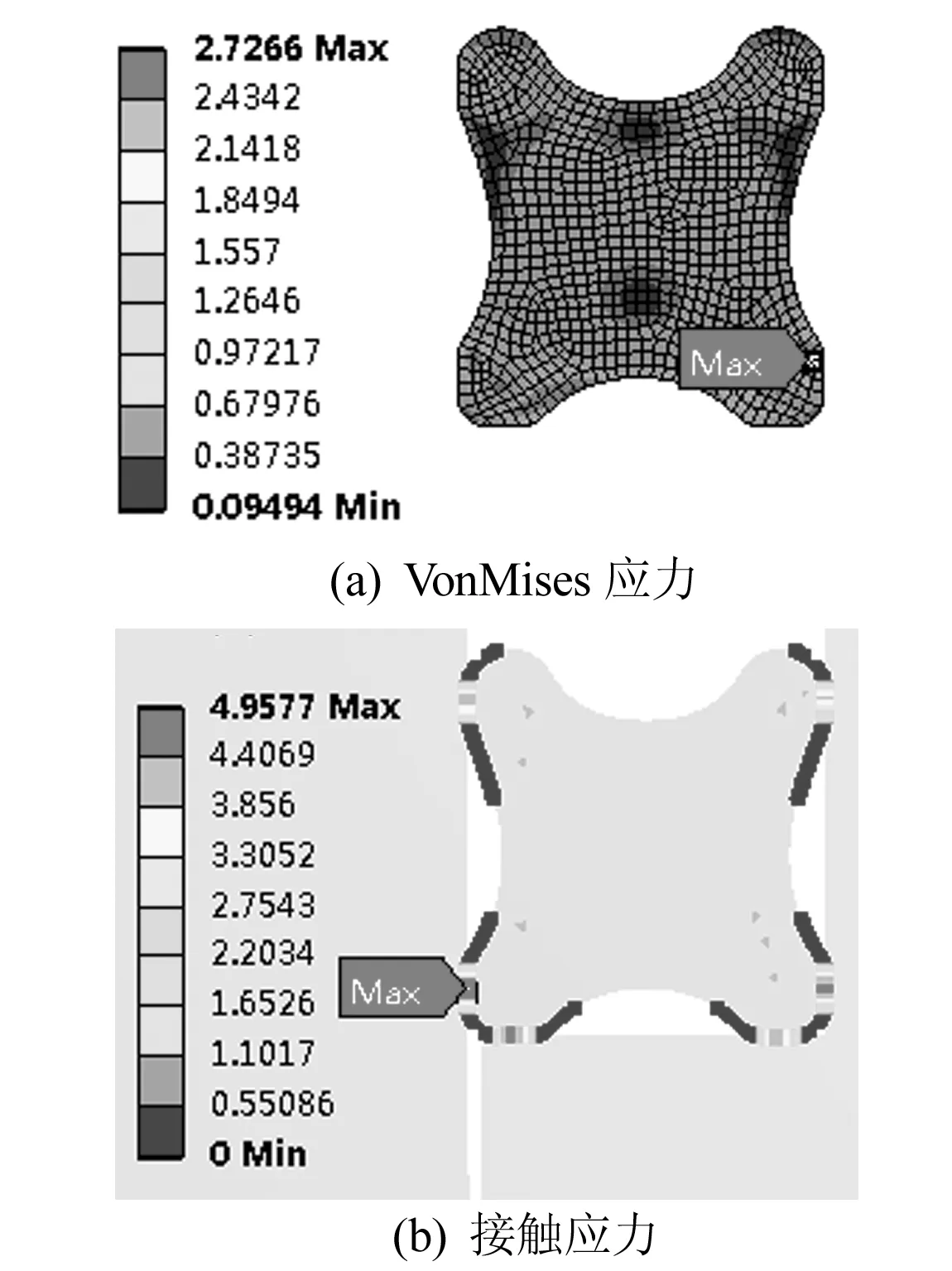
图2 静态密封分析结果
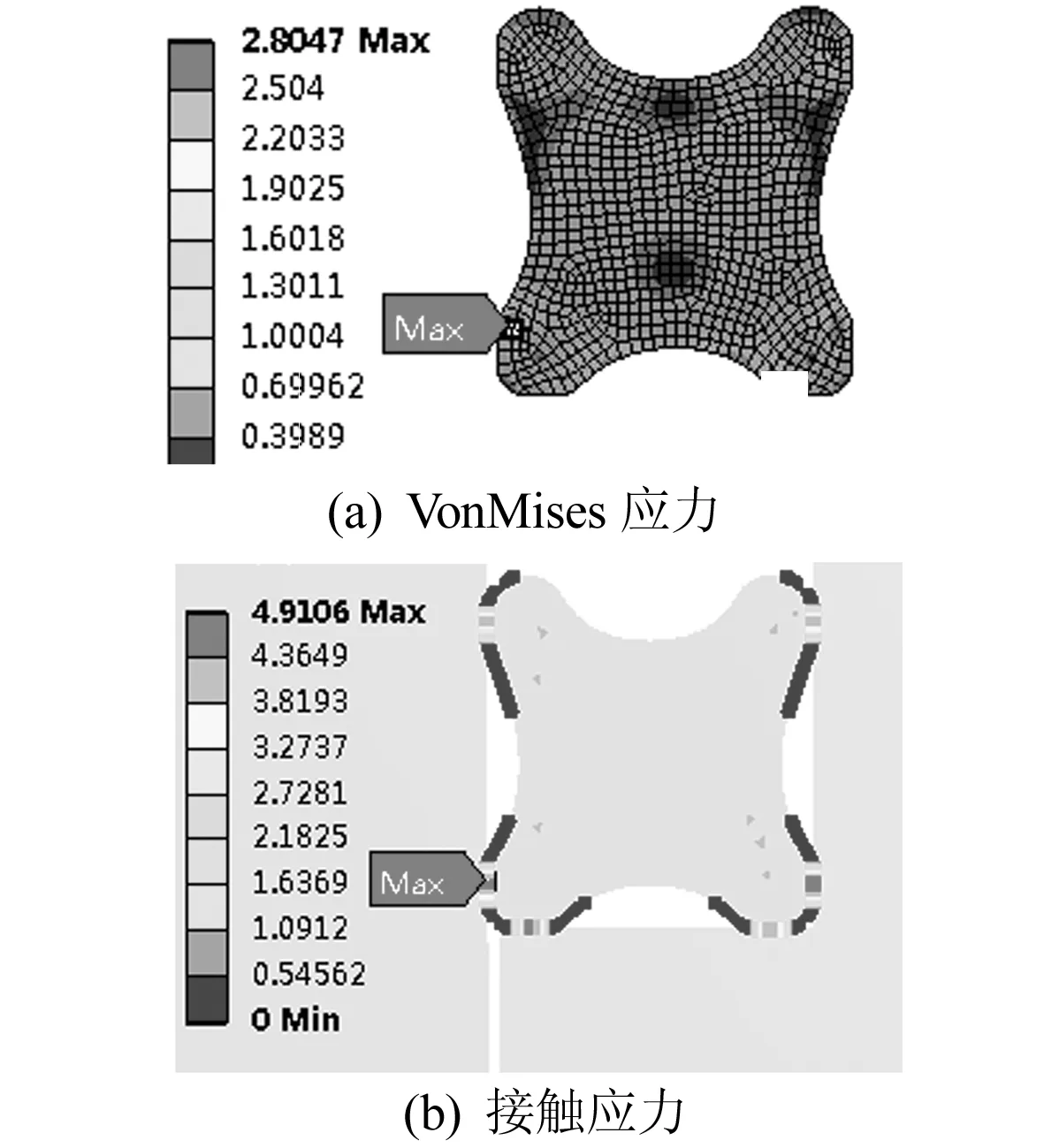
图3 动态密封分析结果
密封圈静态密封分析结果如图2所示,动态密封分析结果如图3所示。根据分析结果,静态和动态密封工况下星形密封圈的VonMises 应力和接触应力变化不大,VonMises 应力均小于3 MPa,低于丁腈橡胶材料抗拉强度,接触应力均在5 MPa左右且均在密封圈与配合零件的接触密封面上,大于工作气压1.2 MPa,能保证良好的密封。
3 星形密封圈优化设计
为了获得星形密封圈截面形状尺寸的优选方案,在初步仿真分析的基础上,以密封圈截面长度、唇边圆弧半径、过渡圆弧半径和预压缩率4个指标作为优化因子,采用响应面优化设计方法来确定最终数值。
根据响应面分析中由2水平正交试验设计方法演化出的中心复合试验设计规则制订了试验方案,试验设计的因素和水平如表1所示。
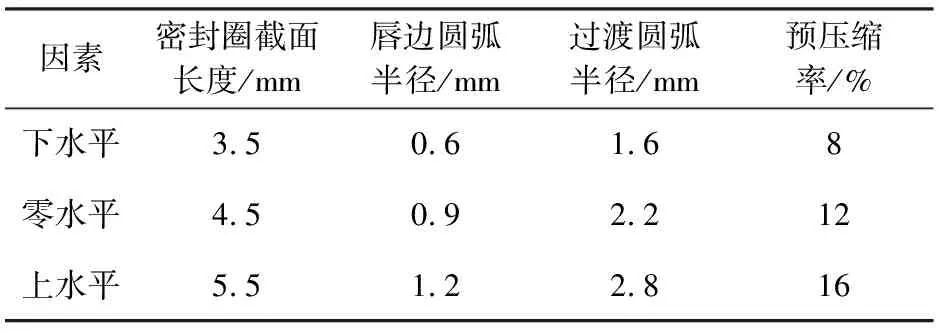
表1 试验设计的因素和水平
对试验方案各组数据逐一进行仿真分析,获得相应的VonMises应力和接触应力数据,采用克里金插值法拟合回归方程模型,绘制响应面曲线,从而建立应力与优化参数之间的函数关系。从试验数据来看,随着变量参数值的变化,VonMises应力和接触应力基本处于同步上升下降趋势;当VonMises应力小于3.5 MPa时,接触应力基本维持在小于6 MPa的水平;当VonMises应力超过3.5 MPa时,接触应力有一个超过10 MPa水平的突变。按照设计要求,原则上以取得VonMises应力极小值,接触应力极大值为最优方案,但是根据初步数据分析来看无法达成上述目标。因此最终确定优化目标的标准为VonMises应力小于4 MPa,接触应力大于10 MPa,按照该原则求解函数,获取最优值。
上述过程均通过专业软件来实现,根据响应面法建立的函数关系抽取10 000组样本数据进行对比分析,最终优选出3组最接近设计目标的数据(见表2)。考虑到低温环境下尺寸变化的影响选取更大预压缩量方案,以及在接触应力相近情况下VonMises应力尽可能低,选择方案2作为最终设计方案,密封圈实物如图4所示。
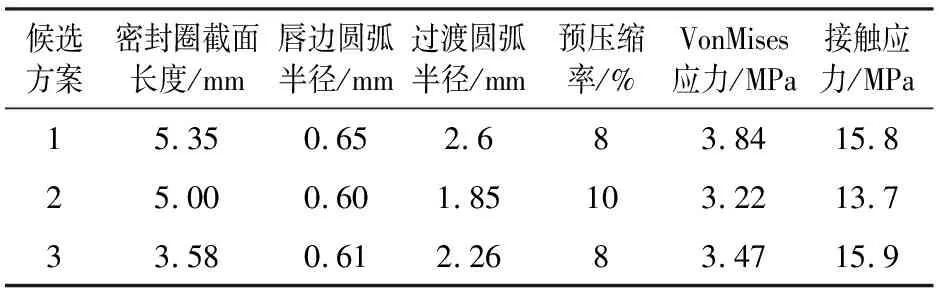
表2 候选设计表

图4 密封圈实物
4 星形密封圈试验情况
采用该密封圈的制动缸经过100万次常用制动缓解动作疲劳试验,10万次停放制动缓解动作疲劳试验,1万次手拉缓解动作疲劳试验,-40 ℃低温动作密封性能试验,IEC 61373标准2类振动冲击试验,各类型式试验后测试制动缸密封性能满足设计要求。
5 结论
通过研究星形圈密封系统,建立了密封圈材料非线性和接触非线性仿真分析模型,结合响应面优化设计方法对密封圈的形状和几何尺寸及装配配合尺寸进行了进一步优化,经过试验证明采用上述方法设计的密封圈能满足制动缸密封要求,对后续产品用星形密封圈的设计应用具有一定的参考借鉴意义。

