视场角限制下导弹协同攻击导引律设计*

赵久奋，史绍琨，尤 浩，杨奇松

(火箭军工程大学 作战保障学院， 陕西 西安 710025)

为有效应对日臻完善的现代导弹防御体系，采取的突防策略之一是控制多枚导弹同时攻击目标[1-2]，实现瞬时饱和攻击；此外，控制多枚导弹以指定角度攻击目标可以实现对目标全方位攻击[3]，提高导弹打击效果。因此，导弹的攻击时间和攻击角度协同控制对实现突防和充分发挥武器效能大有裨益[4]。

目前，关于导弹攻击角度控制的文献已有很多，对导弹攻击角度和时间同时控制的文献则相对较少。文献[5]将建立的导弹运动模型线性化，利用最优控制理论，推导了带有攻击时间和攻击角度约束的制导律。文献[6]通过在比例导引的基础上增加两项偏置项，得到了一种攻击时间和攻击角度控制的偏置比例导引律。文献[7]设计了一种用于角度控制的制导律和一种用于时间控制的滑模制导律，通过制导律的切换实现对攻击时间和攻击角度的同时控制。文献[8]采用模型预测静态规划方法，对用于攻击时间和攻击角度的控制量进行迭代更新，从而满足导弹的攻击时间和攻击角度约束要求。然而上述制导控制方法均未考虑导弹视场角的限制，在末制导段，对导弹攻击时间和攻击角度的控制会使导弹产生大机动，大机动将产生较大的视场角，若不考虑视场角限制，容易导致视场角超过导引头视场角范围而丢失目标。

针对该问题，文献[9]采用多项式函数推导得到了时间控制的导引指令，并以附加反馈项的形式引入一项用于视场角限制的导引指令，实现对导引头视场角的限制和对攻击时间的控制。文献[10]设计了一种可用于攻击角度控制的偏置比例导引律，并将导引律分阶段设计，实现了对导引头视场角的限制。但就考虑导引头视场角限制下协同控制攻击时间和攻击角度的导引律还未见报道。

因此，本文设计了一种新型可用于控制导弹攻击时间和攻击角度的偏置比例导引律，并通过将导引律分阶段设计，使其满足导引头视场角的限制。

1 问题描述

考虑二维平面内导弹攻击静止目标情况，弹目相对运动关系如图1所示。

图1 弹目相对运动关系Fig.1 Relative motion between missile and target

图1中：OXY表示地面惯性坐标系；M和T分别表示导弹和目标；r表示弹目视线；q表示弹目视线角，规定由弹目视线r逆时针旋转到水平基准线时为正；σ表示弹道倾角，规定导弹速度v位于水平基准线上方时弹道倾角为正；φ表示前置角，假设导弹飞行过程中攻角很小可忽略，则导引头视场角近似等于导弹前置角；v表示导弹的速度，假设为常值；an表示导弹法向过载，即导引系统的控制输入。则导引系统模型为：

(1)

(2)

(3)

式(3)中的tgo不能由弹载设备直接测得，需提供一种精准的tgo估计方法。

视场角限制下攻击时间角度控制导引律可以描述为通过设计an，使

(4)

2 攻击角度和攻击时间控制导引律设计

本节针对平面内导弹攻击静止目标问题，设计了一种新型可用于攻击角度和攻击时间同时控制的偏置比例导引律。通过在传统比例导引律的基础上设计两项偏置项，实现对攻击角度和攻击时间的控制，并利用Lyapunov理论证明该导引律下闭环导引系统的稳定性。所设计的攻击角度和攻击时间控制的偏置比例导引律形式为：

(5)

式中，偏置项a1用于对攻击角度的控制，偏置项a2用于调节导弹攻击时间。

2.1 攻击角度控制导引律设计

为使导弹在攻击结束时刻tf以期望角度击中目标，设计导引律结构如下：

(6)

式中，N≥3为比例系数，a1为偏置项用于攻击角度的控制。

式(6)适用于导引系统模型式(1)。将式(6)代入式(1)第四式，得到：

(7)

将式(7)在(t,tf)内积分可得：

(8)

式中，下标f表示攻击结束。当导弹击中目标时，qf=σf。设σd为期望攻击角度，令

σd=σf

(9)

假设a1在(t,tf)内的每一小段时间Δt内均为常值，导弹速度v恒定，则式(8)变为：

(10)

式中，tgo=tf-t为当前时刻的剩余时间。

则攻击角度控制导引律为：

(11)

为方便叙述，将式(11)导引律记为BPN-ACG。在此导引律中，q和σ可通过弹上设备敏感视线角和弹道倾角的变化率积分得到，而tgo不能由弹载设备直接测得[11-12]。由于对攻击角度的控制会使弹道变得弯曲，传统的剩余时间估计方法会产生较大误差[13]。因此，采用文献[14]中的剩余时间估计算法。

(12)

2.2 BPN-ACG下攻击时间控制导引律设计

为使导弹在指定时间以指定角度攻击目标，设计导引律为：

an=anσ+a2

(13)

式中：anσ为前文设计的BPN-ACG，用于使导弹在攻击结束时间tf以指定角度σd攻击目标；a2为将要设计的偏置项，用于调节攻击时间，使导弹的攻击结束时间tf为指定攻击时间td。

将式(13)代入式(11)和式(1)，得到：

(14)

式(3)中的剩余时间tgo将采用BPN-ACG作用下的剩余时间估计式(12)。因为下文将视场角限制在一个小的范围内，所以在小前置角假设下推导的式(12)适用于视场角限制下攻击时间角度控制导引律。

对式(12)求导，并将式(14)和式(1)代入式(12)的求导式，化简后有：

(15)

式中，P(r,v,q,φ,σd,N)为不显含a2的函数。k1和k2的取值为：

P(r,v,q,φ,σd,N)=-1

(16)

对式(2)求导，得到：

(17)

对式(3)求导，并将式(15)～(17)代入式(3)的求导式，得到：

(18)

为使ξ(td)→0，φ(td)→0，考察式(14)和式(18)，设计偏置项a2为：

(19)

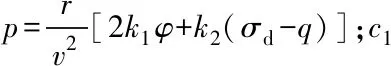
(20)

式中，δ1、δ2都为充分小的正数，且δ2>δ1，δ1、δ2的取值根据计算精度而定。

设计偏置项a2为式(19)的目的是：一方面实现时间控制，另一方面起到限制导弹视场角的作用。当不考虑落角约束时，式(19)将视场角限制在[-φmax,φmax]的范围内，这一特点将在后文设计考虑视场角限制的导弹协同攻击导引律时使用。

至此，得到一种新型攻击角度和攻击时间控制导引律：

(21)

式(21)不能用于对导弹视场角的限制，在实际应用中容易导致视场角超出导引头视场角范围而丢失目标。为方便叙述，记式(21)的导引律为BPN-ATCG。

2.3 稳定性分析

为证明导引律BPN-ATCG能够使r(td)→0，φ(td)→0，ξ(td)→0，构造Lyapunov函数：

(22)

结合式(18)、式(19)对式(22)求导，得到：

(23)

将式(19)代入式(18)得：

(24)

ξ=elnξ0-Ct

(25)

分析式(25)可知，通过调节c1和c2的数值进而调节C的大小，可使t=td时，ξ(td)→0。

考察r的动力学性能：

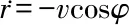
(26)

考察φ的动力学性能：

(27)

参考文献[6]，式(27)中右侧前两项使φ在有限时间内收敛。随着ξ→0，右侧第三项趋于0，即逐渐转为BPN-ACG。所以，在指定攻击时刻td，有φ(td)→0。

3 考虑视场角限制时协同攻击导引律设计

分析BPN-ATCG，假设式(21)中攻击角度控制项为0时可以实现攻击时间控制，并且将视场角限制在[-φmax,φmax]的范围内。因此本节将BPN-ATCG中比例导引项和用于攻击时间控制的偏置项a2一直作用于导弹，始终对攻击时间进行控制；将用于攻击角度控制的偏置项a1设计成三个阶段b1、b2、b3，通过三阶段导引指令的切换，实现对攻击时间和攻击角度控制的同时，将视场角限制在导引头视场角范围内。偏置项a1设计如图2所示。

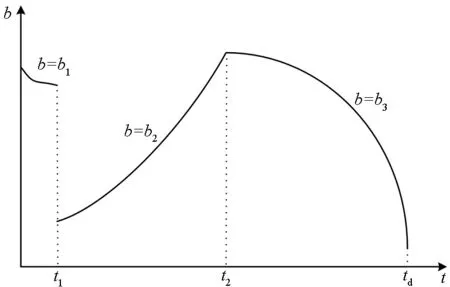
图2 三阶段偏置项示意图Fig.2 Three stage bias terms profile

第一阶段设计导引律an1=an，即导弹按导引律BPN-ATCG飞行。实时判断视场角φ是否超出导引头视场角范围[-φmax,φmax]，若导引过程中视场角φ始终在导引头视场角范围[-φmax,φmax]内，则按导引律式(21)导引直至击中目标；若导引过程中视场角φ在t1时刻达到导引头视场角范围边值，则t=t1时转为第二阶段。

第二阶段设计导引律使视场角φ始终在导引头视场角范围内，导引律形式为：

(28)

将式(28)代入式(1)并求导，得到：

(29)

当φ→±φmax时，式(29)右侧第二项趋于0，该项控制φ∈[-φmax,φmax]。所以只需让式(29)右侧第一项收敛，即

(30)

求解得到：

b2>(1-N)v

(31)

当比例系数N=3时，可取b2=-1.5v。为保证导引指令连续，当t=t2时刻满足b2(t2)=b3(t2)时进入第三阶段。其中b3为第三阶段的偏置项。

第三阶段设计导引律为：

(32)

视场角限制下攻击时间角度控制导引律的导引过程如图3所示。

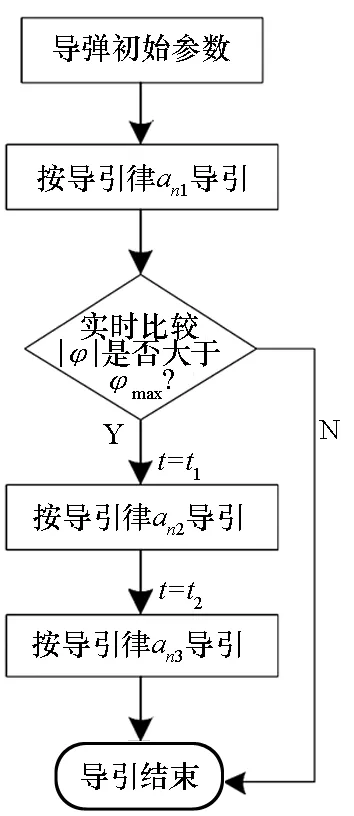
图3 视场角限制下攻击时间角度控制导引流程Fig.3 Impact time and angle control guidance process with field-of-view limit

4 仿真结果与分析

首先分析设计的BPN-TATCG以及提到的其他两种导引律和文献[15]中的导引律的导引效果。参数设置为：导弹初始位置为(-10 000 m,1000 m)，目标位于坐标原点(0 m,0 m)，导弹速度恒为300 m/s，初始弹道倾角为30°，指定攻击角度和攻击时间分别为-90°和43 s，视场角限制为[-45°,45°]，过载限制为8g(取g=9.81 m/s2)，c1=10,c2=2，δ1=0.01,δ2=0.02，仿真步长为0.01 s。分别用BPN-TATCG，BPN-ATCG，BPN-ACG以及文献[15]中带有导引头视场角限制的攻击时间控制导引律BPN-TCG四种导引律进行仿真，得到仿真结果如图4所示。

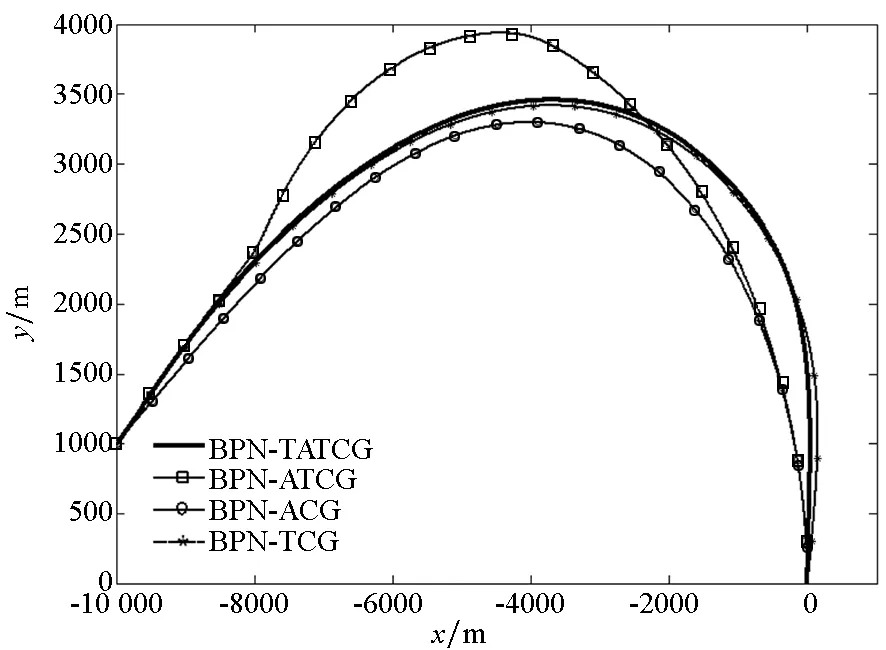
(a) 弹道轨迹(a) Trajectory

(b) 导引指令(b) Guidance law

(c) 视场角(c) Field-of-view

(d) 终端落角(d) Terminal angle图4 四种导引律作用下的仿真结果Fig.4 Simulation results of four guidance laws

从仿真结果可以看出，四种导引律均可以使导弹击中目标，脱靶量都小于0.6 m。BPN-ACG满足落角约束；BPN-TCG满足时间约束；BPN-ATCG同时满足攻击时间和攻击角度约束，但不满足视场角约束；BPN-TATCG可以实现在满足视场角约束下指定时间指定角度攻击目标。

从图4(a)中可以看出，BPN-ATCG作用下的弹道较高，高的弹道会导致大的视场角，这与图4(c)中的结果是一致的。从图4(b)中可以看出，在导引初期除BPN-ACG外的三种导引指令均超过过载限制，这与制导律中的参数c1和c2的取值有关。一般情况下，取一个较大的c1值，调节导引指令使其初期较大，末期较小。从图4(c)中可以看出，相较于BPN-ATCG作用下的视场角超过导引头视场角约束，在BPN-TATCG作用下的视场角到达导引头视场角约束后，通过此时导引指令的切换使视场角始终不超过导引头视场角约束，且收敛至0。从图4(d)中可以看出，除导引律BPN-TCG外，其他三种导引律均满足终端落角约束。

分析多枚导弹协同攻击静止目标的效果，期望多枚导弹在同一时刻以不同落角攻击目标。设置目标位于坐标原点(0 m,0 m)，三枚导弹速度均为280 m/s，因三枚导弹在传统比例导引作用下最长攻击时间为32.3 s，故指定攻击时间为37 s，三枚导弹的初始参数和期望落角如表1所示。

表1三枚导弹初始参数和期望落角

Tab.1 Initial parameters and expected angle of three missiles

导弹初始坐标/m初始弹道倾角/(°)期望落角/(°)M1(-8500,1000)35-90M2(-7000,4000)10-120M3(-5000,7000)-20-150

取g=9.81 m/s2，c1=10,c2=2，δ1=0.01,δ2=0.02，过载限制为8g，视场角限制为[-45°,45°]，仿真步长为0.01 s，则在BPN-TATCG作用下的仿真结果如图5所示。

(a) 弹道轨迹(a) Trajectory

(b) 导引指令(b) Guidance law

(c) 视场角(c) Field-of-view

(d) 终端落角(d) Terminal angle

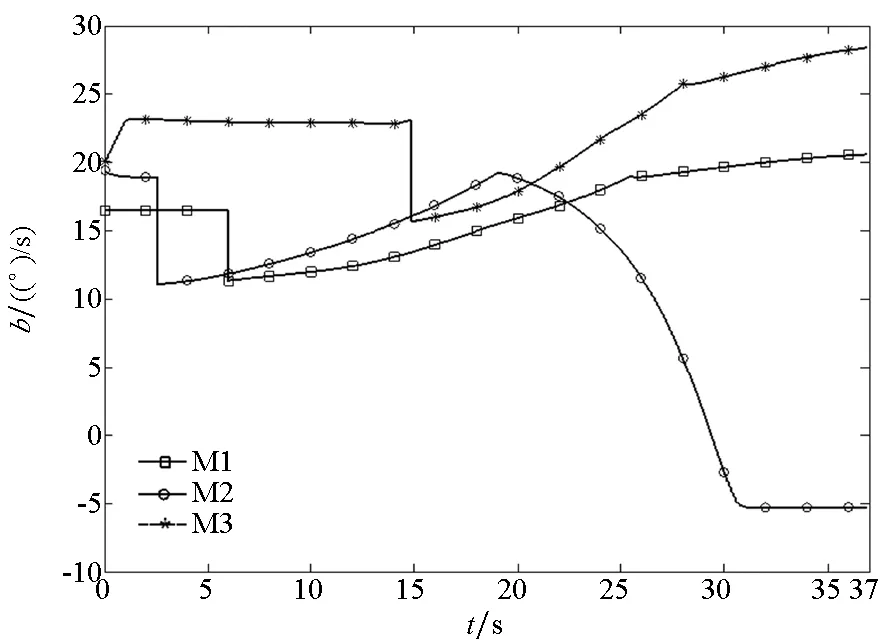
(e) 偏置项(e) Bias term图5 三枚导弹协同攻击目标仿真结果Fig.5 Simulation results of three missiles cooperative attack targets

从图5(a)中可以看出，三枚导弹的攻击时间误差在0.01 s以内，落角误差在0.06°以内，并且都可以击中目标。从图5(b)中可以看出，导弹M3在导引初期导引指令超过过载限制，这是由于M3要求的期望落角较大，为防止在导引末期产生较大过载，通过调节可调参数c1、c2造成的。从图5(c)中可以看出，三枚导弹的视场角在达到导引头视场角约束时，通过导引指令的切换，形成“触底反弹”，从而保证视场角始终在导引头视场角范围内。视场角“触底反弹”的时刻与图5(e)中偏置项的首次切换时刻是一致的。从图5(d)中可以看出，M2、M3导弹分别在导引末段和初段对攻击角度的调节较大，与图5(b)中M2、M3导弹分别在制导末段和初段导引指令变化较大对应。从图5(e)中可以看出，三枚导弹的偏置项各经历了三次切换，第一次切换使导引指令产生了跳变，第二次切换导引指令连续。

5 结论

本文对视场角限制下导弹协同攻击导引律进行了研究。提出了一种新型攻击时间和攻击角度控制的导引律，将导引律分为三阶段，设计视场角限制下的分段导引过程。仿真结果表明：设计的导引律满足导引头视场角约束，制导精度高，对攻击角度和攻击时间的控制能力强。针对不同位置的导弹，可以实现在满足导引头视场角约束下协同作战，具有一定的实际应用价值。但就如何优化过载分布以及如何减弱第一、第二阶段切换时产生的导引指令跳变问题，仍值得进一步研究。