锂电池储能在电磁发射中的应用*

龙鑫林，鲁军勇，魏静波，周 仁，柳应全，吴羿廷

(海军工程大学 舰船综合电力技术国防科技重点实验室， 湖北 武汉 430033)

电磁发射系统连续发射时，脉冲储能系统在顶层控制系统控制下短时大功率向发射装置输送能量，使发射装置在规定长度内加速负载至预定速度[1-4]。如果脉冲储能系统直接从电网取电，对变电站及相应输配电设备要求非常高。以单发总储能100 MJ、射速要求为12发/min的电磁发射系统为例，如果直接从电网取电，其充电需求将达到40 MW，显然舰船平台难以提供如此大的短时脉冲功率，需要通过混合储能技术来解决此问题，与国内普遍采用的、运用于可再生能源的混合储能不同[5-12]，文献[13-15]提出的新型混合储能技术将蓄电池作为脉冲电容器的充电电源。蓄电池在电网与用电设备之间起到能量缓存功率放大作用，有效地降低了大功率连续电磁发射[16-17]对电网的瞬时功率需求的94%。

为了实现蓄电池储能技术应用于电磁发射，本文针对基本储能单元需求进行分析，确定基本储能单元类型为锂电池。在此基础上还需解决：面对舰上不同电磁发射设备电压、电流的需求，需要研究能够实现锂电池组快速灵活串并转换的拓扑结构；由于电磁发射强电磁噪声的复杂条件、放电时序的灵活性和短脉冲大倍率连续放电等特殊工况，导致采用传统算法对单体电池的电池荷电状态(State Of Charge, SOC)估算不准确问题；由于各电池组之间存在不一致性，并联起来放电时可能导致输出电流不均衡，使得本来就处于高倍率放电的电池组超限使用。

1 电磁发射用蓄电池单元需求分析

某电磁发射用蓄电池系统工作过程如图1所示，连续脉冲输出电流，既需要功率也需要能量。

图1 电磁发射系统工作过程Fig.1 Working process of battery system in electromagnetic launch system

因此，在电网与电磁发射设备之间加蓄电池储能环节，主要以满足电磁发射连续工作时巨大能源需求为目的，如图2所示。

图2 电磁发射系统需求示意图Fig.2 Demands of electromagnetic launch system

从图2可以看出，蓄电池在电网与后级用电设备之间起到能量缓存与功率放大的作用。需要高功率密度和高能量密度，初步分析选用锂电池适合此需求。结合实际工程应用对电池的要求如图3所示。

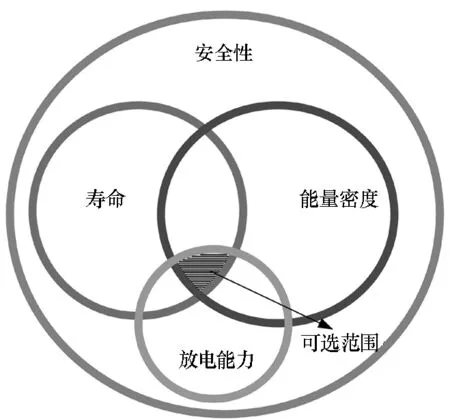
图3 电磁发射系统电池选择范围Fig.3 Range of batteries to be selected for electromagnetic launch system

在安全性的前提下，需兼顾循环寿命、储能密度、放电能力，如果能同时具备四个方面的高指标锂电池，对任何系统都是最理想的储能元件，但实际对比分析四个方面存在一定矛盾，不可能同时具备高指标(见表1)。

表1 几种电池之间的对比

从表1中可以看出：几家公司的放电倍率都较高；三元电池能量密度高于磷酸铁锂电池，但安全性低于后者；能量密度与放电倍率存在矛盾，放电倍率提高时势必降低能量密度。

由于电磁发射用蓄电池每次发射时需要输出较大的瞬时脉冲功率，并不像传统动力汽车注重续航能力，但为了保证一定连续发射次数，在体积重量有限的情况下，需要兼顾一定的能量密度。

通过以上分析，在电磁发射应用背景下侧重于放电能力，因此本文将选用磷酸铁锂路线，开发兼顾能量密度的高放电倍率锂电池。

2 拓扑结构

在电磁发射系统中，采用如图4所示的时序串联电路拓扑，从工作原理、器件参数指标、系统效率、纹波系数等方面都比直流斩波、恒压等拓扑结构更合适[16]。

图4 时序串联放电原理图Fig.4 Scheme of orderly-serial circuit

其中，E1～En为电池组，r0为线路阻抗，r1～rn为蓄电池内阻，K1～Kn为开关，D0为续流二极管，L为限流电感，C为脉冲电容。系统工作原理为：首先闭合第一组蓄电池的开关K11，将第一组蓄电池接入电路中，当脉冲电容C的电压增加到第一组蓄电池E1的输出电压时，充电电流降低。此时，另一组蓄电池E2切换进电路。由于蓄电池组输出电压的增加，充电电流再次增加，直至电容C的充电电压再次和两组触发了的蓄电池总电压相等，此时触发下一组蓄电池，依此类推。本文试验平台所采用的模型参数如表2所示。

表2 试验平台模型参数

仿真的蓄电池时序入网时间计算方法如下。对照图4建立电路方程：

(1)

根据表2，rn=33.3 mΩ，r0=50 mΩ，限流电感L=50 mH。由各已知参数可知，满足：

(2)

电路为欠阻尼，从而求解式(1)得：

I(t)=Ceα1(t-tn)(α1k1+β1k2)cosβ1(t-tn)+

Ceα1(t-tn)(α1k2-β1k1)sinβ1(t-tn)

(3)

u(t)=eα1(t-tn)[k1cosβ1(t-tn)+k2sinβ1(t-tn)]+En

(4)

式中：

k1=u(0)-En

(5)

k2=[I(0)/C-α1(u(0)-En)]/β1

(6)

α1=-(Rn+R0/2L)

(7)

(8)

其中，I(0)，u(0)为当前阶段电路初始状态。任一新阶段的初始条件为上一阶段(每串联一组电池入网为一个新阶段)最后时刻电流、电压值。第一组蓄电池串联入网时，初始值已知为I1(0)=0、u1(0)=0。对式(4)求导得：

(9)

只需通过式(9)求解电流峰值所对应的时间值tmax，从而求解电流峰值Imax，并使蓄电池在串联入网时电流峰值等于370 A即可计算出各电池组的入网时间节点。按上述方法计算得到放电电流电压曲线如图5所示。

(a) 电流曲线(a) Current curve

(b) 电压曲线(b) Voltage curve图5 时序串联放电曲线Fig.5 Current and voltage curves of orderly-serial

观察图4和图5可知，采用此拓扑结构只能实现恒流(每组电池输出最大电流)对脉冲电容线性升压充电，对于不同的用电设备，需要蓄电池输出不同的电流和电压，此结构难以满足要求，需要研究一种能够实现电池组灵活串并的拓扑结构。

图6 改进电路结构Fig.6 Circuit configuration of amelioration scheme

图6为改进电路原理示意图，可实现电池组串并联结构切换，图左边是主正主负母线，E1～En电池组既可以通过开关K21～K2(2n)、K31～K3(n-1)、K41～K42实现时序串联，也可以实现任意组并联，从而满足不同输出电流电压需求。

仍以电容为负载，先两组电池并联，再进行时序串联，采用与前述相同的方法求解电路，得到在此情况下的电容器充电电流I(t)、电压u(t)与电流峰值Imax、各电池入网时序，仿真结果如图7所示。

(a) 电流曲线(a) Current curve

(b) 电压曲线(b) Voltage curve图7 优化方案仿真波形Fig.7 Simulation curve of amelioration scheme

从图7可知，改进后的电路拓扑结构可实现更大放电电流，充到设定电压所需时间可缩短一半。

另外考虑到电池的不一致，容易出现并联不稳定或无法实现的问题，在并联之前采用两步骤来克服：①单体电池不一致性导致电池寿命缩短，甚至扩散影响同组的其他电池。由于单体电池在同一电池组中和其他电池充放电工况一样，即使用一致性可以保证，唯一导致同一电池组内单体电池不一致的是由于电池本身特性和出厂匹配，可以通过出厂质量和工艺控制来降低不一致的概率，实际表明这一方法的有效性，再者通过计算出各节电池的SOC，出现同一电池组内明显不一致的单体电池，需进行均衡充电；②单组电池不一致会导致并联不稳定或无法实现问题，上面已提到正常单体电池SOC基本代表本组电池的SOC，直接反映电池组之间的一致性，如果相差较大，可通过充电机给电池组充电进行均衡，使SOC基本一致，再通过均衡装置进一步均衡后可保证稳定并联。因此下文将围绕准确计算SOC和电池组均衡方法展开研究。

3 蓄电池组SOC估算问题

锂离子电池的SOC作为评估电池剩余电量的重要指标，是实施蓄电池组精确管理的重点，也一直是锂电池行业研究的热点和难点。锂离子电池SOC估算的方法主要有开路电压法[18]、安时积分法[19]、智能算法和组合算法。开路电压法基于开路电压与SOC之间的关系曲线，根据不同的放电倍率和环境温度分别查表，但该方法需在电池静置较长时间后才能采集，且估算精度依赖于电压采集的精度；安时积分法是目前最广泛应用的方法，但该方法存在累积误差，估算精度局限于初始SOC值、电流测量精度和电流平稳性；智能算法很大程度上依赖于精确的数学模型和大量的历史数据进行，可自适应地辨识模型参数之间的非线性关系，有关研究表明，扩展卡尔曼滤波法[20]和神经网络算法[21]可提供较高的估算精度；组合算法是根据SOC区间或使用工况采用两种或者两种以上估算方法进行组合或加权计算的方法，目前在电动汽车用电池管理系统(Battery Management System, BMS)上使用较为广泛的是“开路电压法+安时积分法”。

由于电磁发射环境复杂，电压传感器和电流传感器都不可避免地受到强电磁噪声干扰，且由于电流脉冲短、倍率高、单体数量众多，单纯依靠直接测量方法进行估算存在高频噪声和采集频率受限等问题，使得对单体电池进行电流采集和积分变得异常困难且估算精度堪忧。因此，电磁发射用蓄电池系统的SOC估算应以蓄电池组为管理对象，建立单个蓄电池组的戴维南等效电路模型(见图8)，以实时采集的电池组电压和放电电流作为模型输入，在数学模型基础上进行模型参数的辨识计算。在估算出蓄电池组的SOC后，再结合单体电池的电压差异和内阻差异进行修正，计算出单体电池的SOC。针对单体电池SOC不一致的问题，采用主被动均衡策略，以实现单体电池的状态一致性。

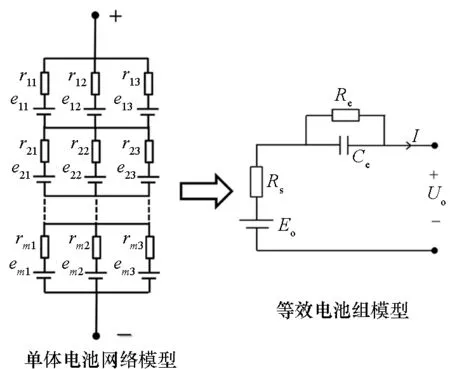
图8 等效电池组模型Fig.8 Equivalent battery group model

等效电池组模型中，Eo为蓄电池组平衡电动势；Uo为电池组端电压；Rs为等效内阻；Re和Ce分别表示等效电阻和等效电容，表征蓄电池组的极化特性。为了更准确地描述蓄电池的容量特性和容量衰减规律，一种较好的建模方法是将其等效为一个容值呈非线性变化的大电容，这种模型即是“新一代汽车合作计划(Partnership for a New Generation of Vehicles, PNGV)”模型[22](见图9)。由于采用先进的拓扑结构和控制策略[16]后，放电电流纹波较小，PNGV模型在电磁发射用瞬时大电流工况下同样适用。

图9 PNGV电池模型Fig.9 PNGV battery model

图9中，Vdcv为蓄电池组的放电截止电压，Cp用于描述负载电流的时间累积产生的开路电压变化。蓄电池组的SOC可用下式表示：

(10)

式中：Cp1和Cp0分别是SOC处于高区间和低区间的等效电容量；Vccv表示蓄电池组的充电截止电压。采用式(10)计算SOC的优势是不需要知道初始SOC是多少，由于Eo可通过静态时直接测量开路电压得到。等效电容量Cp可通过下式在长时间尺度内计算得到：

(11)

采用图4所示的电路拓扑结构进行连续电磁发射仿真分析，以某一蓄电池组为例进行SOC辨识。在2～4 s、6～8 s和10～12 s连续进行三次电容器充电试验，仿真得到的蓄电池组端电压V(t)曲线和放电电流I(t)如图10所示。

图10 蓄电池组端电压曲线和放电电流曲线Fig.10 Terminal voltage curve and discharging current curve of battery group

采用式(11)辨识的某一蓄电池组SOC辨识结果和辨识误差如图11所示。可以看出，采用该方法可较好地辨识蓄电池组的SOC值。

(a) SOC辨识结果(a) SOC identification results

(b) SOC辨识误差(b) SOC identification error图11 SOC辨识结果和误差Fig.11 SOC identification results and error

4 电池组放电不均衡问题

从前文可知，电池组E1～En按顺序接入主回路中放电，每次都是E1放电时间最长，En放电时间最短，因此各电池组存在不均衡状态，如电池组并联放电，势必导致本来就处于高倍率放电的电池组超限使用。假设并联放电的两组蓄电池的端电压分别为250 V和260 V，采用表2中模型参数，仿真可得两组蓄电池的放电电流波形(见图12)。

图12 未均衡之前电池组放电电流波形Fig.12 Current curve of two battery groups before balance circuit is used

由图12可知，未均衡之前两组电池并联放电会存在不均衡现象。前面提到先计算出各组电池SOC，并通过充电机进行均衡充电使SOC基本一致，但还并不能完全保证稳定并联。因此本文提出一种电池组均衡方法来保证电池组之前完全一致，如图13所示。

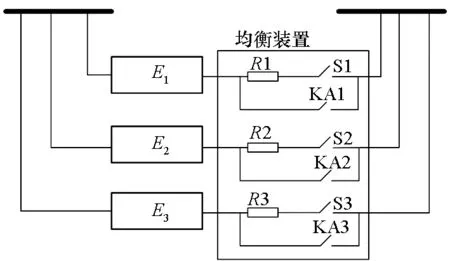
图13 电池组均衡电路Fig.13 Balance circuit of battery groups

在非工作状态下，闭合开关S1、S2、S3，电池组间进行均衡；当防环流工装检测到R1(或R2、R3)两端电压为0 V(小于100 mV)时，自动闭合KA1(或KA2、KA3)；待均衡完成后拆除防环流工装，安装电池组与铜排间的连接电缆。

均衡之后的电池组放电曲线如图14所示，基本吻合一致，消除了放电不均衡现象。

图14 均衡之后电池组放电电流波形Fig.14 Current curve of two battery groups after balance circuit is used

以上相关测试在锂电池测试平台中完成。平台包括了18组260 V锂电池，以及200 mF电容器。

5 结论

为解决电磁发射系统连续工作时巨大电能需求，本文针对锂电池储能关键技术展开研究，首先结合系统需求确定高倍率锂电池研究方向；通过优化系统结构，实现蓄电池组串并转换，满足不同用电设备电压电流输出需求；采用PNGV模型以整个蓄电池组为研究对象，动态辨识蓄电池组SOC；针对蓄电池组并联放电不均衡问题，提出了均衡策略，保证并联电池组输出一致性。随着后期新型蓄电池的研发，配合系统结构的进一步优化，锂电池储能必将在连续大功率电磁发射的储能部分中体现出更强大的优势。