地铁车辆用永磁同步电机的转速控制

(石家庄铁道大学 电气与电子工程学院，河北 石家庄 050043)

随着科学技术的发展，永磁材料从最初在军工、航天领域的应用逐渐转到实际生产生活中。从家用小电器到空调压缩机，以及近年来迅速发展的电动汽车等，都与永磁材料有关。永磁同步电机(permanent magnet synchronous motor，PMSM)具有高功率密度、高转矩密度、高效率等优点，引起了轨道交通领域应用单位和制造商的广泛关注[1-2]。近年来，随着城市轨道交通的发展，地铁车辆驱动系统中的牵引电机越来越多地使用永磁同步电机[3-6]。2011年沈阳地铁2号线某列车装载2台永磁同步电机(1台使用，1台备用)，2016年试运营的长沙地铁1号线某列车，成为我国首列全车装载永磁牵引电机并投入载客运营的地铁列车。将永磁同步电机应用到地铁车辆中，减少了列车的体积和质量，也提高了运营效率。

地铁车辆电机的调速性能直接关系到乘客乘车舒适度。目前关于永磁同步电机调速的研究有很多[7-12]，一些智能控制算法也被提出，比如模糊控制、神经网络以及模糊自抗扰控制等。虽然它们在一定程度上提高了调速性能，但是其缺点和局限也不可忽视[13]，主要表现在，模糊控制依据经验制定模糊规则和选取隶属度函数，缺少相应理论依据，神经网络容易出现效果不稳定、过拟合，应用于工程实际比较困难，模糊自抗扰控制在高阶控制参数优化方面有待深入研究。

传统比例积分控制要求系统模型精确且对负载扰动敏感，已不能满足永磁同步电机的高性能需求[14]，因此使用算法优化比例积分控制器参数是当前研究的热点[15-16]。

本文中使用随机搜索算法优化比例积分控制器参数，步骤简单，能同时优化多个参数并快速逼近最优值，实现了永磁同步电机快速响应和平稳转换。

1 永磁同步电机的数学模型

1.1 坐标变换

矢量控制通过坐标变换将复杂的交流永磁同步电机数学模型等效成直流电机模型，然后用直流电机的控制策略进行控制，最后经过坐标反变换重新得到原来模型。

1.1.1 Clark变换

从三相静止坐标系(abc)到两相静止坐标系(αβ)的变换，其变换矩阵(Tabc-αβ)为

(1)

1.1.2 Park变换

从两相静止坐标系(αβ)到两相旋转坐标系(dq)的变换，其变换矩阵(Tαβ-dq)为

(2)

由式(1)、(2)可得abc坐标系到dq坐标系的变换，其变换矩阵(Tabc-dq)为

(3)

式中θ为转子位置角。

1.2 永磁同步电机的数学模型

永磁同步电机多变量，耦合性强且各变量成非线性关系。为了便于分析，作如下假设以简化永磁同步电机数学模型：

1)不计电机漏磁和涡流损耗；

2)忽略电机铁心饱和；

3)转子上无阻尼绕组；

4)定子各绕组互差120°；

5)无高次谐波。

由于永磁同步电机定子绕组一般采用Y形连接，因此在dq坐标系下，永磁同步电机电流、电压、磁链和转矩方程为

(4)

(5)

φsq=Lsqisq,

(6)

φsd=Lsdisd+φf,

(7)

(8)

式中：usd、usq为dq轴定子电压；isd、isq为dq轴定子电流；φsd、φsq为dq轴定子磁链；Lsd、Lsq为dq轴电感分量；φf为永磁体磁链；pn为极对数。

永磁同步电动机的运动方程为

(9)

式中：J为转动惯量；Te为电磁转矩；TL为负载转矩；B为阻尼系数；wr为电机机械角速度；w=pnwr为电角速度。

2 永磁同步电机控制系统结构图

由永磁同步电机在dq下的数学模型可知，对永磁同步电机的转速控制就转化为对电流分量isd、isq的控制。因为永磁体磁通不变，所以调速系统中将电流励磁分量isd设为0。同时，isd=0也可保证用最小的电流幅值得到最大的输出转矩，并使转矩波动小[17]。当isd=0时，式(8)简化为

(10)

可见，电机的电磁转矩Te只和电流分量isq有关，所以控制isq就可以控制电磁转矩Te。

永磁同步电机矢量控制系统结构图如图1所示，主要包括电机模块、坐标变换和空间矢量脉宽调制(space vector pulse width modulation，SVPWM)模块及比例积分控制模块等。矢量控制系统内环为电流环，外环为速度环，这样可以提高控制精度，减小误差干扰。电流环作为永磁同步电机矢量控制系统的内环，具有抑制启、制动电流，加速电流的相应过程的作用，同时电流闭环还能改造电机对象的模型，实现励磁分量和转矩分量解耦，得到等效的直流电机模型。

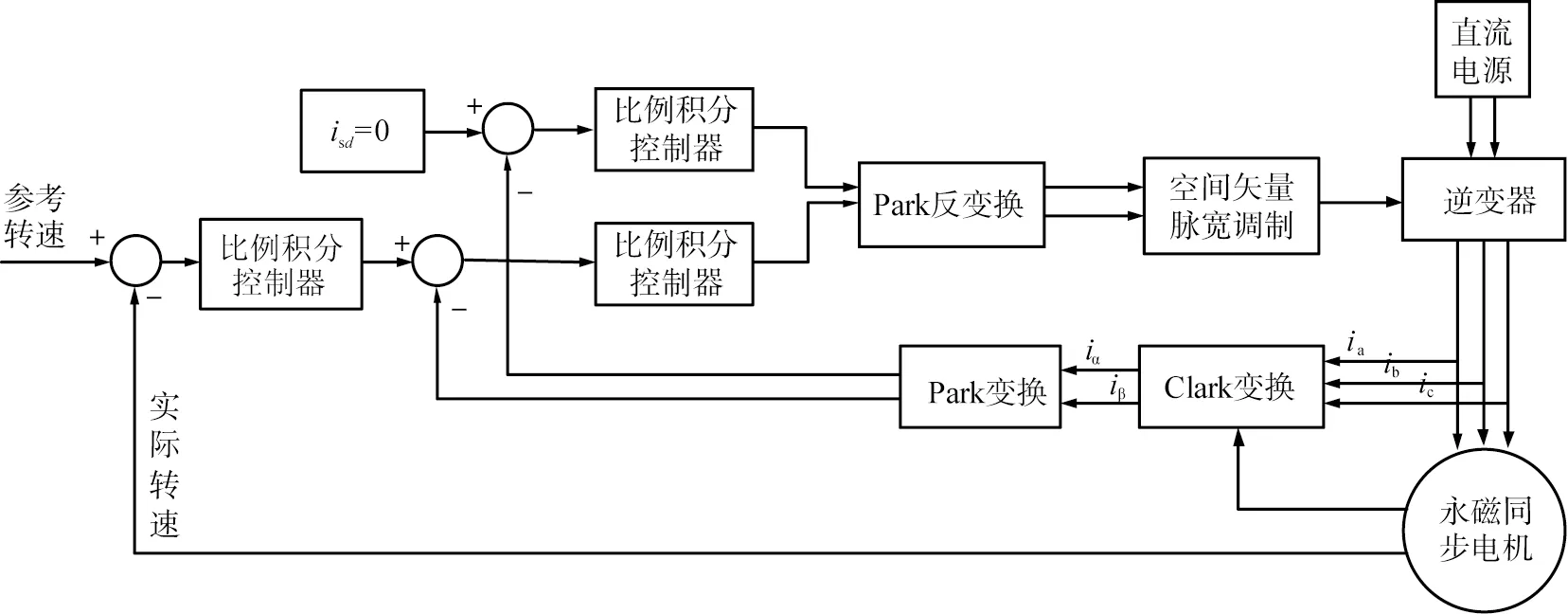
图1 永磁同步电机矢量控制结构图

转速环作为双闭环控制系统的外环，将检测到的电机转速和给定的参考转速相比较，得出两者误差，然后经过速度比例积分控制器进行调节，输出结果作为q轴的电流指令信号isq，d轴的电流指令信号为isd=0。比例积分控制器的传递函数G(s)为

(11)

式中：Kp为比例系数；Ki为积分系数。

3 基于随机搜索算法的控制器参数优化

控制器的参数对控制系统的控制灵敏度和控制精度有很大影响，因此需要用优化算法优化比例积分控制器的参数。随机搜索算法通过在规定的搜索区间内采用随机搜索的方式获取区间次优值，然后把次优值作为下一次寻优的初值进行进一步搜索，直到搜索到满意的结果。该方法简单易行，能同时优化多个参数。

随机搜索算法优化永磁同步电机矢量控制系统中比例积分控制器参数的流程如图2所示。

随机搜索算法优化永磁同步电机控制系统比例积分控制器控制参数的基本步骤如下。

1)将实际转速与参考转速的均方根误差(Re)最小和超调量(δ≤5%)作为性能指标，对控制系统中比例积分控制器的控制参数寻优整定。均方根误差和超调量分别按式(12)、(13)计算。

(12)

式中：Xi表示各采样点的实际转速；X表示参考转速；n为采样点的个数。

(13)

式中：h(tp)表示实际转速中第1个波峰值；h(∞)为参考值；tp为峰值时间。

2)确定控制器参数个数、初值和搜索范围。设转速环、d轴电流环和q轴电流环比例积分控制器的比例、积分系数分别为a(i)，i=1，2，…，6。设a(i)初值为a(0)(i)，在初值a(0)(i)2倍范围搜索。搜索范围记作r(1)(i)，则

r(1)(i)=2a(0)(i)。

(14)

3)随机生成2 000个数，数值在(-0.5，0.5)之间，将其用一个100行20列的矩阵Yk×j表示，其中k=1，2，3，…，100，j=1，2，3，…，20。

首先，从矩阵Y的第1行的20个数里面随机选出6个随机数，记作Y1i，i=1，2，…，6。按式(15)计算待确定的控制参数的值：

a(1)(i)=a(0)(i)+X1i·r(1)(i)。

(15)

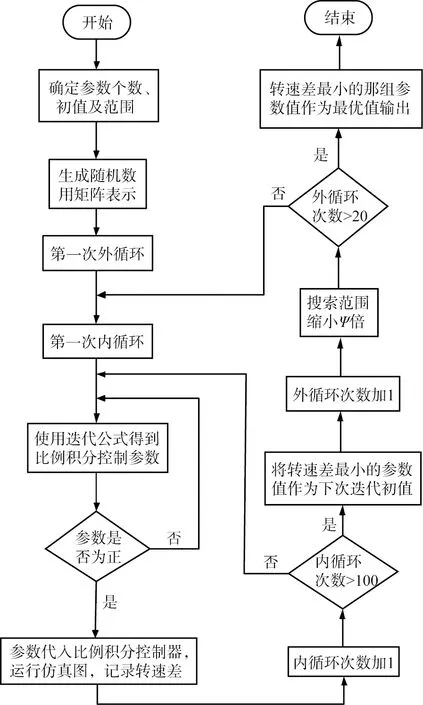
图2 随机搜索算法优化控制器参数流程图

由式(15)分别得到3个比例积分控制器的比例、积分控制系数。

4)将式(15)得到的控制系数作为第2次参数优化的初值，然后从矩阵Y的第2行的20个数里面随机选出6个随机数，记作Y2i，i=1，2，…，6，并按式(15)进行计算，直到k取到100，完成第1次循环，循环20次，从中得到最优结果。

该步骤是一个循环迭代的过程，所以可以用如下通式表示：

(16)

式中：k=1，2，…，100；j为迭代次数，j=1，2，…，20。

5)为了提高收敛速度，节省运算时间，每完成一次迭代后，将搜索范围r(i)缩小ψ倍，即

r(j)(i)=ψr(j-1)(i),

(17)

式中ψ=0.981j1.34。

4 永磁同步电机矢量控制系统仿真与分析

在MATLAB/Simulink平台搭建永磁同步电机矢量控制系统仿真模型，研究系统动态响应。整个系统的仿真模型如图3所示。仿真条件和电机参数的选取分别列于表1、2中。

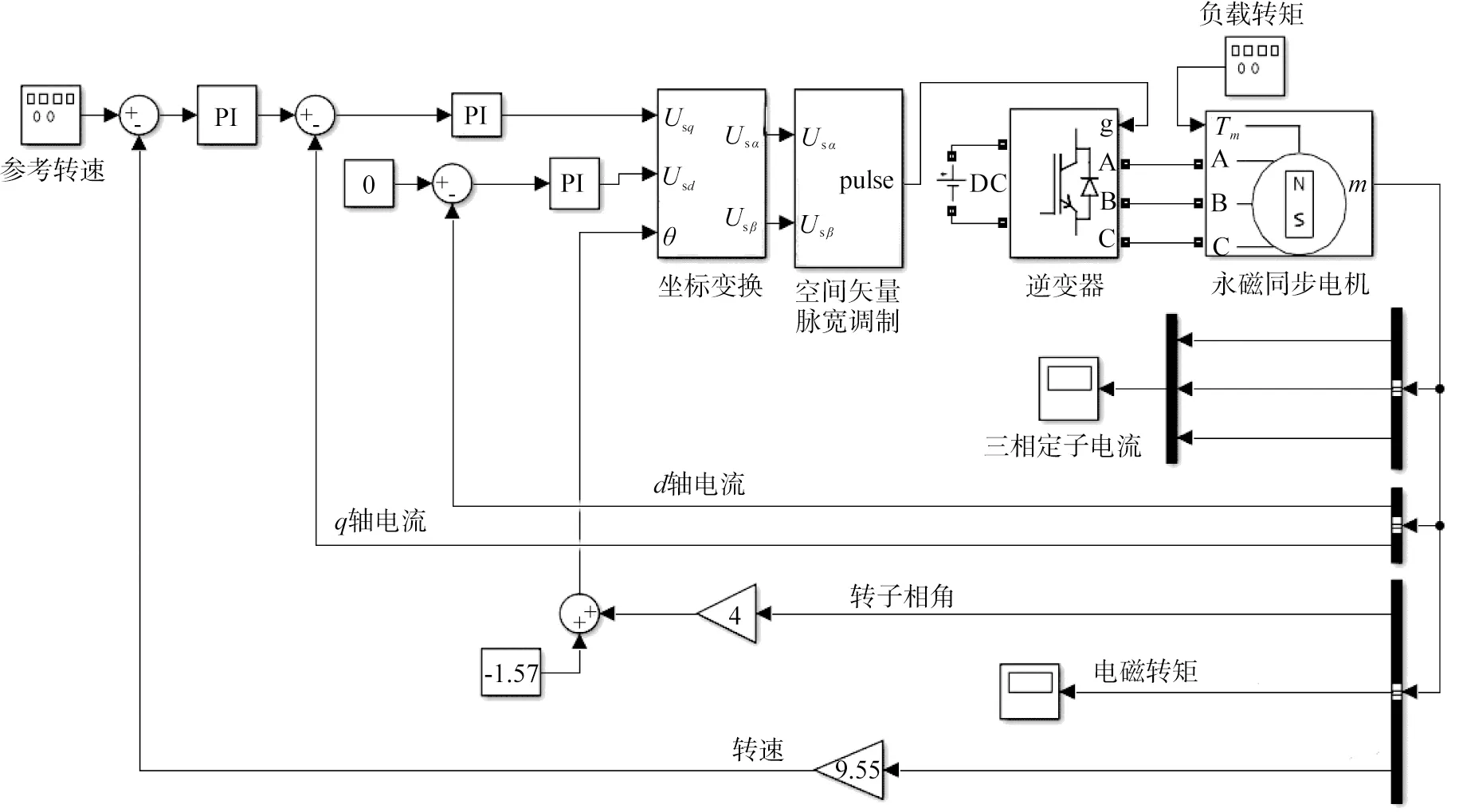
PI表示比例积分控制器；pulse表示脉冲信号；DC表示直流电源；A、B、C表示输入到永磁同步电机的三相电压；Tm表示负载转矩；m表示永磁同步电机的输出量。图3 仿真模型

表1 仿真条件

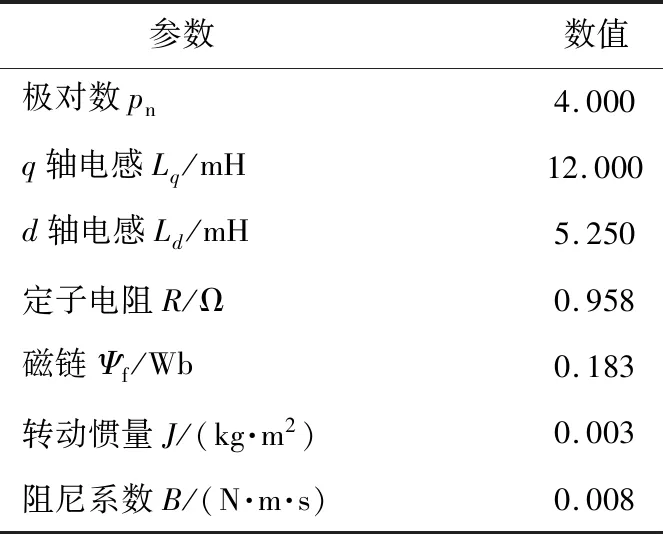
表2 电机参数

给定转速环比例积分调节器的控制参数为Kp1=0.14，Ki1=7；q轴电流环比例积分控制器的参数为Kp2=13.2，Ki2=1 053.8；d轴电流环比例积分控制器的参数为Kp3=57.75，Ki3=1 053.8。将上述参数代入仿真模型里面并运行，得到永磁同步电机空载和负载时的转速波形如图4所示。

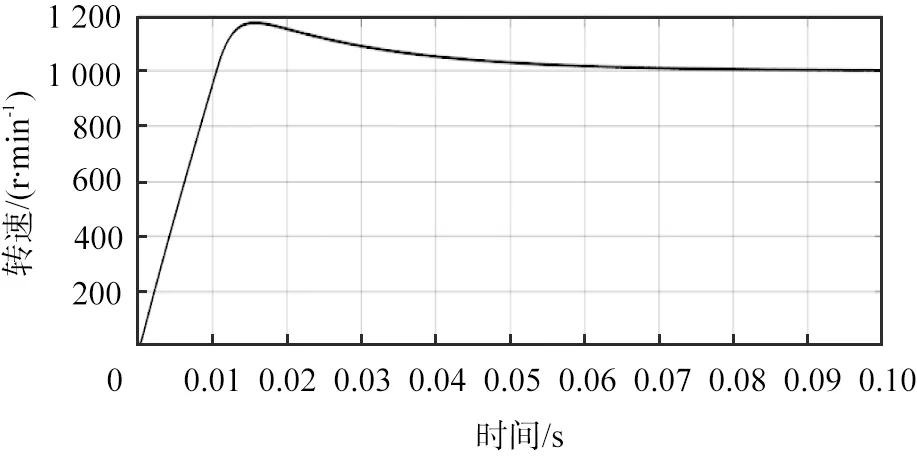
(a)空载时

(b)负载时图4 转速波形仿真结果

虽然电机在启动约0.07 s后稳定到参考转速1 000 r/min，但是转速的超调量达到将近20%，长期如此会降低电机的使用寿命。显然，比例积分调节器的参数并不是最优的，还需要通过优化算法得到新的比例积分控制器的参数，从而获得最优的控制效果。

使用直接搜索算法得到一组转速环、d轴电流环和q轴电流环的比例积分控制器的比例、积分参数分别为Kp1=1.904 0，Ki1=0.169 8；Kp2=13.23，Ki2=1 050.17；Kp3=57.59，Ki3=1 053.18。将参数代入仿真图，得到空载和负载时转速的仿真曲线如图5所示。

(a)空载时

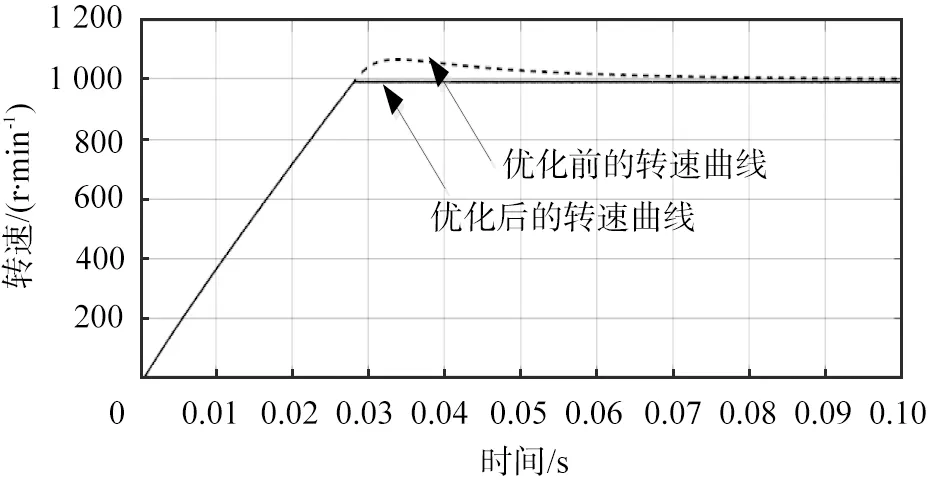
(b)负载时图5 优化后的转速波形

由图5可知，控制系统比例积分控制器控制参数寻优后的转速仿真曲线超调量与之前相比大大降低，几乎为0。空载时，电机启动后在0.01 s时间内快速稳定在参考转速1 000 r/min，比控制系统比例积分控制器控制参数寻优前稳定的时间0.07 s缩短了0.06 s。永磁同步电机加上的负载启动，大约需要0.028 s的时间稳定到给定转速，所用时间也比之前大大减少。如图6所示的参考转速与实际转速差值的曲线也能说明，控制系统比例积分控制器控制参数寻优后的转速曲线要远远好于控制参数寻优前的仿真曲线。

(a)空载时

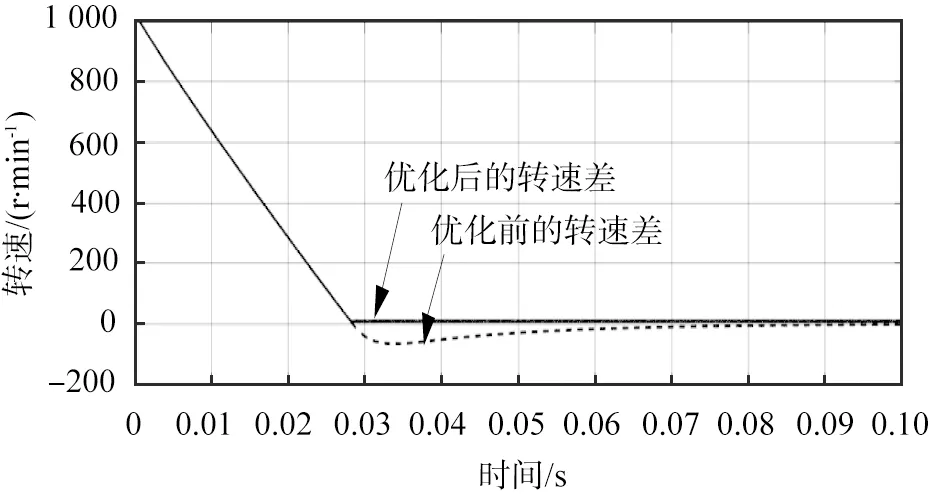
(b)负载时图6 优化后的转速差

如图7所示为永磁同步电机定子三相电流曲线，其中图7(a)为空载时的定子三相电流，图7(b)为负载时的定子三相电流。由图7(a)可知，虽然在启动时电流脉动比较大，但在0.01 s之后就趋于稳定。由图7(b)可知，加入负载后定子电流虽然比空载时稳定时间变长，但在0.03 s也就稳定下来。

(a)空载时

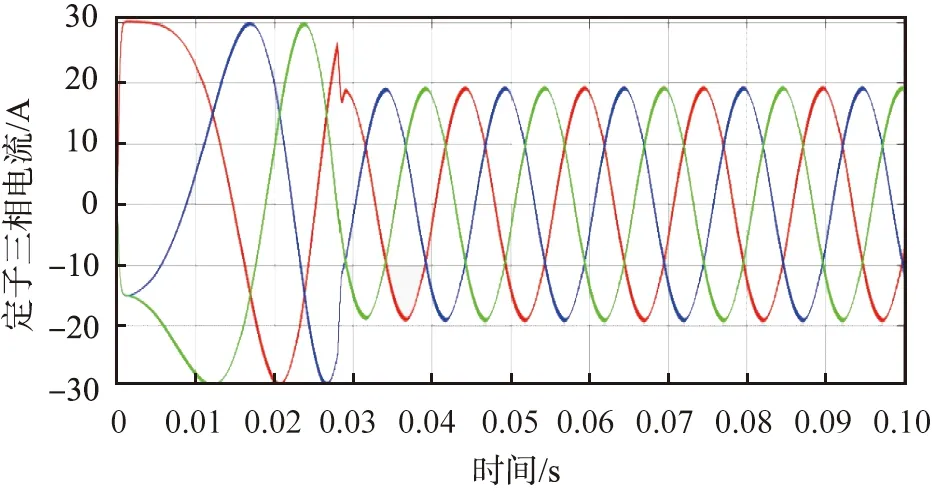
(b)负载时图7 定子三相电流

如图8所示为电磁转矩响应曲线。从图中可以看出，在电机启动初期，电磁转矩有波动，但空载时约0.012 s时电机进入相对稳定状态，负载时大约在0.028 s时就能达到电磁转矩与负载转矩平衡，转矩响应效果良好。

(a)空载时

(b)负载时图8 电磁转矩响应曲线

由以上分析可得，当给定的参考转速为额定转速时，无论是在空载时还是在负载时都能通过使用优化算法得到很好的控制结果。考虑到将永磁同步电机应用到地铁车辆的实际情况，现根据地铁车辆实际运行的工况进行仿真，模拟其启动、匀速行驶、加速行驶以及制动等工况。由于地铁车辆在区间的实际运行时间比较长以及仿真系统的限制，因此将仿真时间缩短。

首先，设置启动转速为1 800 r/min，并在0.05 s时开始加速，达到3 200 r/min时匀速运行，整个过程中空载运行，得到的转速、三相定子电流和电磁转矩响应曲线如图9所示。由图9(a)可以看出，PMSM从转速为0开始启动，经过0.02 s稳定到1 800 r/min，然后匀速行驶。在0.05 s时开始加速，大约在0.068 s时稳定到3 200 r/min，加速时间为0.018 s。与之相对应，由图9(b)、(c)可以看出，三相定子电流也在0.02 s时稳定于某一数值，在加速过程也能体现，以及电磁转矩曲线随着转速的稳定也稳定到0，这与空载情况一致，说明电磁转矩曲线能很好地响应负载转矩。

(a)转速波形

(b)定子电流波形

(c)转矩波形图9 永磁同步电机实际运行时的仿真波形

下面对负载工况下永磁同步电机的运行情况进行仿真。为了使仿真效果明显，仿真时间设为0.4 s，只模拟2个车站及区间的运行。在t=0时，假设负载转矩为15 N·m，规定参考转速为2 500 r/min，稳定后匀速运行到0.12 s，在0.12 s时开始减速，0.135 s时速度减到0。在t=0.2 s时，列车启动，假设此时负载转矩为10 N·m，此区间线路较长，给定参考转速为3 000 r/min，稳定后匀速运行到0.35 s，然后减速到0，得到的仿真波形图如图10所示。由图可知，转速波形无超调，转换平稳，定子三相电流曲线和电磁转矩曲线也根据转速曲线的变化快速响应。

(a)转速波形

(b)定子电流波形

(c)转矩波形图10 负载工况下永磁同步电机运行时的仿真波形

5 结语

采用基于随机搜索算法的矢量控制思想，优化永磁同步电机控制系统中比例积分控制器的参数。将永磁同步电机控制系统的仿真模型在MATLAB/Simulink平台上搭建并仿真。通过分析和比较仿真结果，使用基于随机数直接搜索算法优化控制系统比例积分控制器参数后，仿真系统能够使转速的超调量降低并快速稳定到参考转速。该方法在将永磁同步电机应用到地铁车辆转速控制系统中取得满意的结果。