基于一种新显式时间积分算法的场地 非线性地震反应分析1

赵 密 王亚东 高志懂 段亚伟 杜修力

（北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124）

引言

关于场地地震反应的分析已有大量研究成果（Hashash 等，2010），研究表明土壤在地震作用下会表现出材料非线性效应（Joyner 等，1975；Huang 等，2001；Arslan 等，2006；Hosseini等，2012）。等效线性化方法（Schnabel 等，1972；Idriss 等，1992；Bardet 等，2000；王笃国等，2016）是一种频域方法，通过在不同土体应变条件下选择等效阻尼比和剪切模量，将非线性问题转化为线性问题。当采用材料非线性本构模型描述土体非线性时，需采用时间积分算法求解非线性动力有限元方程。时间积分算法可分为隐式方法和显式方法（Crisfield，1991；Chopra，2009）。隐式算法（栾茂田等，1992；Chopra，2009）每时刻需求解线性代数方程组，计算效率相对较低，如Wilson-θ 法和Newmark 法等。显式算法无需求解线性代数方程组，适合于强非线性和自由度数目较大的问题。研究者已提出多种显式时间积分算法（Chung 等，1994；王进廷等，2002；Belytschko 等，2014）。作者Zhao 等（2019）近期提出一种二阶精度的单步显式算法，该算法适合变时步问题，在线弹性范围内稳定性较好。本文将该算法推广至求解非线性动力有限元方程中，并将其应用于地震波垂直入射时非线性地震反应分析。

1 非线性动力有限元方程的显式时间积分算法

2 地震波垂直入射时场地非线性地震反应分析

本节将上述非线性有限元方程的显式时间积分算法应用于地震波垂直入射时场地非线性地震反应分析中。假定基岩为线弹性半空间，考虑基岩上覆土层的材料非线性，不考虑土体阻尼。在土层下部设置黏性边界条件模拟半空间基岩的辐射阻尼，并在该处以等效结点力的方式实现地震动输入。

计算模型见图2，选取A 点作为观测点。土体非线性材料本构模型选取邓肯-张模型（Duncan 等，1970），土体线弹性参数见表1（杜修力等，2016），杜修力等（2016）未给出配套的非线性参数，故算例中的非线性参数参考实际情况选取，后续研究中将使用更真实表现土体非线性行为的本构模型及真实工程场地参数。算例中的大气压参数取100kPa，内摩擦角增量取0°。入射地震动分别选取狄拉克脉冲和实测地震动（Gilroy Array #3，Coyote Lake, 1979）。入射狄拉克脉冲见图3，观测点结果见图4，实测地震动见图5，观测点结果见图6。图4、图6 中给出采用中心差分法的计算结果作为参考解，由图4、图6 可知，本文算法与中心差分法计算结果吻合较好，说明本文算法的有效性。

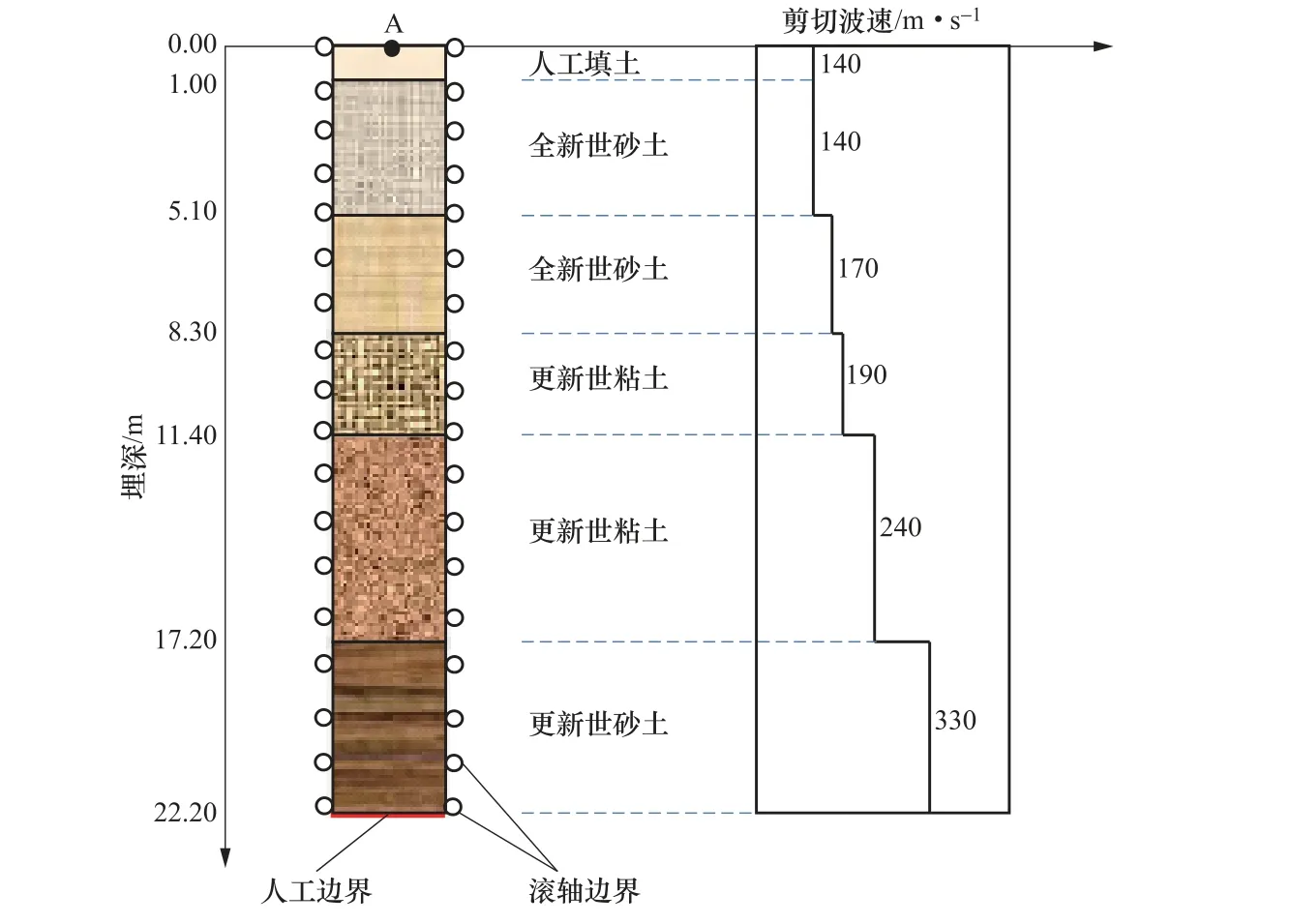
图2 大开车站沿线土层纵断面构造 Fig.2 Site condition of the Daikai subway station in vertical direction

表1 土层参数 Table 1 Parameters of soils

图3 狄拉克脉冲速度和加速度时程图 Fig.3 Velocity and acceleration time history of the Dirac pulse

图4 狄拉克脉冲入射时场地反应分析结果 Fig.4 Results of site analysis under the incident of Dirac pulse

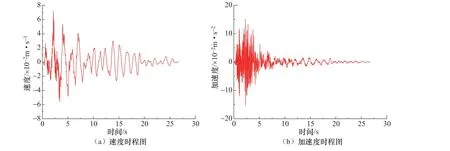
图5 实测地震动速度和加速度时程图 Fig.5 Velocity and acceleration time history of the seismic motion

图6 实测地震动入射时场地反应分析结果 Fig.6 Results of site reaction analysis under the incident of the seismic motion

3 结论

本文发展一种求解材料非线性结构动力学方程的显式时间积分算法，并应用于地震波竖直入射时非线性地震反应分析中，通过算例验证了该方法的有效性。该显式算法具有无需对角阻尼矩阵、单步、稳定性良好等优点。本文考虑了邓肯-张非线性弹性本构模型，下步研究可考虑将该显式算法扩展到弹塑性本构模型及更能反映土层真实变形的本构模型中。