城市轨道交通近轨吸声矮墙降噪量数值仿真分析

周红梅，卜炬鹏，朱万旭，2，高逸豪，罗 涛

(1.广西科技大学土木建筑工程学院，广西柳州 545006；2.广西建筑新能源与节能重点实验室，广西桂林 541004；3.湖南省建筑科学研究院，长沙 410011)

近年来城市轨道交通在我国发展迅猛，截止至2017年12月31日，中国内地累计有34个城市建成投运城轨线路5 021.7 km；2017年新增石家庄、珠海、贵阳、厦门4个运营城市；新增33条运营线路，868.9 km运营线路长度新增线路再创历史新高，比2016 年新增线路534.8 km增加334.1 km，增幅达62.5%[1]。

城市轨道交通的迅猛发展不可避免地带来了严重的噪声污染。轨道交通列车行驶引起的噪声是重污染源，对沿线居民和行人都有很大干扰。世界健康组织(WHO)的报告指出[2-4]，长期生活和工作在噪声源环境下，比如生活在工厂、轨道交通枢纽附近，虽然人的感官感受可能会逐渐适应这种长期的噪声环境，但人体自身并不会对这种日常的噪声环境产生适应。相反，日积月累暴露在噪声中，对于人体会造成更大的损伤。

目前的轨道交通降噪措施(图1)按其基本原理可以大致划分为两类。一是主动降噪，即降低轮轨振动，减少噪声源产生的噪声；二是被动降噪，即在噪声传播的途径和接受处对噪声进行削弱[5]。虽然我国在主动降噪方面的研究也日益成熟，但以被动降噪来降低轨道交通噪声在我国仍是十分经济有效的方式，其中声屏障(图1(a))技术在我国被广泛应用。声屏障是控制传声途径的重要措施，其主要功能是阻挡和吸收噪声，仅留部分噪声绕射过去，而在屏障后形成声影区，从而降低噪声。我国目前使用的声屏障通常高度大于3 m，虽然能有效地降低列车通过时产生的噪声，但是同样带来了一些不便。例如，声屏障体积过大，不论是车内乘客还是沿线两侧的居民，其视线均被高大的声屏障所遮挡，产生不必要的压抑感；由于其体积过大，需要更多的安全距离，通常安装在距离轨道中心4 m的水平距离外，浪费了宝贵的城市空间；声屏障过大的体积，在生产运输过程中需要使用较多的材料，产生较大的生产以及运输成本；轨道沿线的声屏障，在列车出现事故，需要紧急停车疏散车内乘客时，有可能成为乘客逃生的巨大阻碍[6]。

我国迫切需要一款轻巧、体积小的近轨吸声矮墙(图1(b))声屏障填补这一领域的市场空白。为此笔者通过检索大量相关文献，分析了我国轨道噪声的主要组成部分以及频率特性，在此基础上，参考国外设计经验[7]，对近轨吸声矮墙进行设计。以我国目前城轨交通中最宽的A型车作为设计基准，根据相关标准中关于限界的规定，以及隔声量质量定律，依次推导出了近轨吸声矮墙的安装位置、高度以及厚度的设计计算方法，并以此设计了一种近轨吸声矮墙。

图1 降噪措施

本次设计采用复合形式，所设计的近轨吸声矮墙表面为150 mm 厚的陶粒混凝土吸声层，背面为50 mm 厚的自研高性能混凝土隔声层，如图2所示[8]。本文借助Virtual.Lab平台，用声学间接边界元法计算不同顶部形式近轨吸声矮墙，在不同受声点处的降噪能力，为今后在实际工程中的吸声矮墙优化设计提供参考。

图2 近轨吸声矮墙单元模型(单位：mm)

1 Virtual.Lab软件简介

为解决振动噪声方面的问题，比利时LMS公司早年开发的Sysnoise软件被广大工程技术人员接受并应用。随后LMS公司以CATIA V5平台为基础，研发了CAE软件Virtual. Lab，其中包括Acoustic、Motion、Vibration、Durability等模块，可以实现构建几何模型、有限元前处理、有限元分析、结构振动特征分析、结构振动声学分析等一系列仿真运算。

声学模块Virtual. Lab Acoustic基于Sysnoise软件发展而来，它不仅完全继承了Sysnoise的强大功能，并且在其基础上衍生出包括FEM完美匹配层、快速多极BEM、FEM、BEM流体声学等技术。

本文使用的为Virtual. Lab12版本，用到以下几个模块。

(1)几何建模(Geometry)：该模块基于法国达索公司的CATIA V5开发，在软件界面以及使用方法上与CATIA V5保持一致，无需额外安装CATIA软件。

(2)网格划分(Meshing)：网格划分工具具有强大的功能，结合基本的和先进的自动网格划分功能，以及基于线框、曲面及几何实体生成有限元模型。

(3)声学分析(Acoustic)：在本文中，声学有限元(Acoustic Harmonic FEM)以及声学边界元(Acoustic Harmonic BEM)这两个模块将被使用到。

2 不同顶部结构的近轨吸声矮墙的降噪量计算

2.1 近轨吸声矮墙降噪量仿真介绍

近轨吸声矮墙的降噪效果用插入损失IL来评价，即声场内一受声点处，在有近轨吸声矮墙时和没有近轨吸声矮墙时，二者声压级之差，其表达式如下

IL=ΔLd-ΔLt-ΔLr-(ΔLs，ΔLG)max

(1)

式中，ΔLd为吸声矮墙的绕射声损失，dB(A)；ΔLt为吸声矮墙的透射声损失，dB(A)；ΔLr为吸声矮墙的反射声损失，dB(A)；ΔLs为地面障碍物衰减损失，dB(A)；ΔLG为地面吸收衰减损失，dB(A)。

目前国外除了直板式近轨吸声矮墙外，还有少量其他具有不同顶端结构的吸声矮墙。利用Virtual. Lab分析不同的顶部结构近轨吸声矮墙的降噪量(插入损失)，该问题属于外声场问题。利用FEM法进行计算时，将需要分析的声场进行离散化，对于外声场问题而言，这增大了前期建模划分网格的工作量，也增加了计算所需的时间。而间接边界元法(Acoustic Indirect BEM)在分析外声场问题只要在所需的位置建立划分声学面网格，并施与其对应的边界条件，故本文采取该方法来对此问题进行仿真分析。

2.2 仿真模型的建立

(1)声学场点的建立

在现场实测近轨吸声矮墙插入损失时，需要利用麦克风传声器记录受声点在安装矮墙前后的声压级值。在仿真分析中，利用划分场点的方式来记录不同位置的声压级值，每一个场点节点相当于一个麦克风传声器。

以城市轨道交通的轨道为中心的水平半径30 m范围为研究对象，以两根轨道中心为对称轴，取轨道一侧作为分析区域。如图3所示，为了同时得到水平方向和竖直方向上不同点的声压级值，在水平方向上，取34 m×10 m的平面，分别在长宽的方向上以0.5 m为单位长度划分网格，得到1 449个场点节点，该场点代表轨道顶部所在水平面；同时在竖直方向上，也建立34 m×10 m场点，以同样的单位长度划分网格。

图3 场点网格划分示意

(2)声源的选取

根据文献[8]，在水平场点上，距离预定放置近轨吸声矮墙声学模型945 mm处，插入沿场点宽方向上的柱面声源。综合考虑参考相关文献[9-10]中所测得的我国轨道交通噪声源强参数，对该声源激励进行赋值定义，声源参数如图4所示。

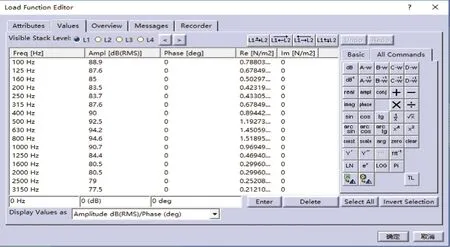
图4 声源源强参数

(3)近轨吸声矮墙声学模型的建立

以平面场点宽度为参照，取所研究的近轨吸声矮墙总长度为10 m；参考声屏障目前几种较常见的顶部结构，分别建立直板式、“倒L”式、“T”式、折板式、“Y”式、圆弧顶式6种不同形式的近轨吸声矮墙模型，其中6种矮墙在竖直方向上的高度均为824 mm，即为前章节所设计的有效高度，模型如图5所示。

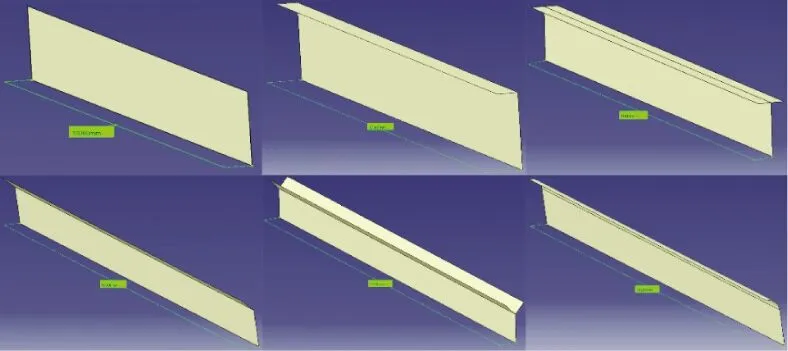
图5 不同顶部形式的近轨吸声矮墙

由于所研究的频域上限为3 150 Hz，分别对所建立的不同矮墙模型进行自由面网格划分，网格单元长度设为17 mm，将所划分网格类型定义为声学网格。并对其进行声学前处理，赋予其流体材料属性。

最后，在水平面场点下插入对称平面(Symmetry Plane)代表刚性地面(图6中绿色部分)。以直板式近轨吸声矮墙为例，所建立声学计算模型如图6所示。插入Acoustic Response Case求解器，设置计算区间为100～3 150 Hz，计算步长设置为区间上16个1/3倍频程中心频率。

图6 BEM插入损失声学仿真模型

2.3 仿真计算结果

(1)不同近轨吸声矮墙在不同受声点处的插入损失

取2组受声点作为研究对象，其中第一组受声点根据国际标准ISO3095选择。该标准指出： 如果被测车辆的上部存在重要声源，则第二网格推荐置于轨道顶部以上3.5 m的高度处距轨道中心线7.5 m处。列车顶部的受电弓在列车行驶时会产生气动噪声，是一个重要声源。除7.5 m处受声点外，分别再取大于和小于7.5 m的受声点各1个。该组有3个受声点，高度均为高出轨道面3.5 m，其中第一个点A距离轨道中心3.5 m，第二个点B距离轨道中心7.5 m，第三个点C距离轨道中心25 m。

第二组取路边行人为研究对象，该组有3个受声点，高度选取为高出轨面0.5 m。其中第一个点A′距离轨道中心3.5 m、第二个点B′距离轨道中心7.5 m，第三个点C′距离轨道中心25 m。

分别提取第一组和第二组节点在不同情况下的声压级值，代入EXCEL进行计算后，分别得到A、B和C三点处不同的降噪量(插入损失)，进行下一小节的结果分析。

(2)针对受声点A、B和C的结果分析

通过分析近场距离受声点A，发现在A受声点处，几种形式近轨吸声矮墙的插入损失值都不太理想，造成这种现象的原因主要是：对于离轨道中心3.5 m时，A点3.5 m的高度已经高出近轨吸声矮墙声影区范围2.35 m以上，极大削弱了近轨吸声矮墙在这个受声点处的降噪能力。针对城市轨道交通噪声峰值频域500～800 Hz，“Y”式近轨吸声矮墙在A点拥有更好的插入损失值。

通过分析中距离场受声点B，发现在B受声点处，近轨吸声矮墙的插入损失有显著提高。且在低频段内的160 Hz处，所有吸声矮墙都有较好的插入损失值。对于直板式近轨吸声矮墙，除了在400，500 Hz处出现较小插入损失值，其余频段波动不大，基本符合插入损失值随频率上升而上升的趋势，且在噪声峰值频率800 Hz处达到了10.28 dB(A)；“倒L”式的矮墙插入损失整体波动同样不大，对于目标频域的降噪能力比直板式有一定的提升，其中800 Hz处达到13.01 dB(A)；折板式矮墙降噪能力随频率波动较大，有一定的频率选择性，其插入损失峰值位于1 250 Hz，达到24.18 dB(A)，次峰位于800 Hz，达到18.32 dB(A)；“Y”式矮墙在500 Hz以及800～2 000 Hz拥有较强的降噪能力，仅次于折板式；而对于“T”式和圆弧顶式矮墙，其综合频段降噪能力与直板式吸声矮墙相差无几。针对城市轨道交通噪声峰值频域500～800 Hz，“倒L”式近轨吸声矮墙在此处拥有更好的插入损失值。

通过分析远场受声点C，所有近轨吸声矮墙在低频段100～315 Hz的降噪能力极弱。但是对于远声场而言，当没有设置吸声矮墙时，所有频段下该点的声压级已经衰减到70 dB(A)以下。

所有形式的吸声矮墙在该受声点的插入损失波动形式基本保持一致，且峰值均在2 000 Hz处，此时倒“L”式矮墙的插入损失最大，为29.61 dB(A)。针对城市轨道交通噪声峰值频域500～800 Hz，所有形式的矮墙降噪量均达到10 dB(A)以上，其中 “Y”式近轨吸声矮墙在此处拥有更好的插入损失值。

(3)针对受声点A′、B′和C′的结果分析

通过分析近场受声点A′，可以发现所有近轨吸声矮墙的降噪效果相对于在A点有显著提升。对于噪声峰值频率800 Hz处，最低的插入损失值为直板式，为13.28 dB(A)，其他形式的近轨吸声矮墙在该处的插入损失均有5 dB(A)以上的提升，且圆弧顶式在该处达到峰值28.05 dB(A)；对于低频部分，“T”式和“Y”式近轨吸声矮墙拥有更大的插入损失值。针对城市轨道交通噪声峰值频域500～800 Hz，圆弧顶式近轨吸声矮墙在此处拥有更好的插入损失值。

通过分析中距离场受声点B′，可以发现所有近轨吸声矮墙的降噪效果相对于在B点有所提升，所有吸声矮墙在160，400，630，1 600 Hz处均有明显的插入损失峰值，其中“倒L”式矮墙在这几个频率拥有最高的插入损失值。对于直板式，除了500 Hz处出现了较低的插入损失值，在400 Hz后基本随频率增加而增加，其在800 Hz的插入损失值为12.926 dB(A)；“倒L”式矮墙的降噪能力具有最强的频率选择特性，该类型在800 Hz处插入损失为11.92 dB(A)，峰值为1 600 Hz处的26.68 dB(A)；“T”式与折板式在全频段与直板式矮墙的降噪能力波动方式基本保持一致，但在大部分频率相比直板式都有提高，且折板式的提高量更多；“Y”式吸声矮墙在2 500 Hz处降噪效果不佳，但其在该处的插入损失值波动最为平缓，在315～2 000 Hz基本保持逐渐上升，该区间内最低插入损失值为10 dB(A)，且“Y”式近轨吸声矮墙在800 Hz拥有最好的降噪能力16.70 dB(A)；圆弧顶式吸声矮墙插入损失值波动模式与直板式类似，在2 500 Hz处获得了峰值48.43 dB(A)，但是在800 Hz处仅有9.65 dB(A) 针对城市轨道交通噪声峰值频域500～800 Hz，“倒L”式近轨吸声矮墙在此处拥有更好的插入损失值。

通过分析远场受声点C′，可以发现与C处相比，所有近轨吸声矮墙在低频段的插入损失值同样不理想，但在250 Hz之后的区间基本都明显有所提高。直板式吸声矮墙在500～800 Hz拥有较好的降噪能力，其中800 Hz处达到17.29 dB(A)；倒“L”式矮墙在此处的降噪能力整体不佳，其降噪量峰值在2 000 Hz处，为29.65 dB (A)，且在该频率远大于其他形式矮墙；“T”式在500～800 Hz拥有最好的整体降噪能力，且800 Hz处达到18.97 dB(A)，大于其他形式矮墙，且在2 500 Hz以后其降噪能力也大于其他形式矮墙；折板式矮墙在500～800 Hz降噪能力与直板式相差无几，其插入损失峰值为21.77 dB(A)，位于1 250 Hz；“Y”式近轨吸声矮墙在630 Hz和1 250 Hz处有较高的插入损失值，均大于21 dB(A)，但在其他频率上的插入损失值较低；圆弧顶式近轨吸声矮墙插入损失值波动平缓，基本随频率增大而增大，其在500～800 Hz处的插入损失值平均在10 dB(A)左右。针对城市轨道交通噪声峰值频域500～800 Hz，“T”式近轨吸声矮墙在此处拥有更好的插入损失值。

3 仿真计算与经验公式计算的结果对比

如图7所述工况，即受声点位于轨道附近，利用经验公式(2)，计算得到所设计直板式近轨吸声矮墙的插入损失，见表1。

式中，δ为声程差，δ=A+B-C，m，其中A为噪声源距离障碍物顶部的直线距离，B为障碍物顶部距离受声点的直线距离，C为噪声源与受声点之间的直线距离，见图7；f为噪声频率，Hz；c为声速，通常取340 m/s。

图7 声程差示意

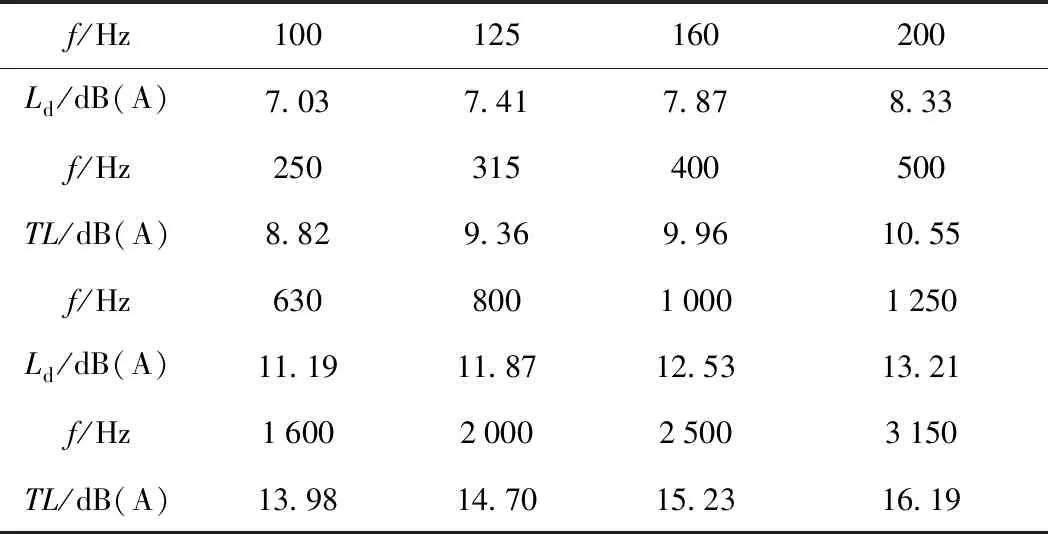
表1 受声点距离轨道中心7.5 m时的绕射声损失

如图8所示，在全频段上，所设计的近轨吸声矮墙降噪量(插入损失)仿真计算结果基本符合随频率上升而上升的趋势。其中在400 Hz频率以上区间，仿真计算结果与公式计算结果吻合度较好，可以认为，利用经验公式法和仿真分析法预测近轨吸声矮墙的降噪量时，在相对较高的频段区域均拥有较高的准确率。

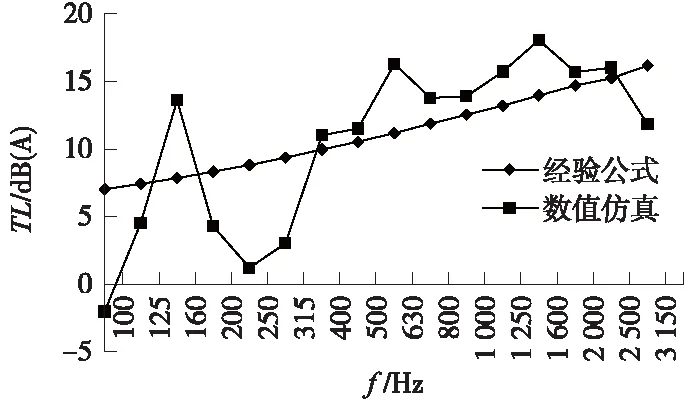
图8 公式计算与仿真计算的结果对比

但在频率低于400 Hz区间，仿真计算结果波动较大，与公式计算结果吻合度较差。造成这种现象的可能原因如下：本次仿真模型将地面作为全反射面处理；而在低频段，噪声波长较长，与地面发生较强的反射现象。在利用经验公式计算插入损失时，通常对于较高频段的降噪量预测更为准确。可以认为，针对低频段区域的降噪量预测，还需要经过后期的实际实验来与公式及仿真结果进行对比，更进一步优化仿真的参数可靠度来获得更加可靠的预测值。

4 结论

(1)对Virtual. Lab软件进行简单介绍，指明本次模拟需要使用到的功能和模块；并系统阐述声学数值仿真的基本原理，即求解Helmholtz方程，以及如何推导该方程，求解该方程所需要的方法和相应的边界条件，以及内外声场、耦合与非耦合问题的分类。

(2)使用声学边界元法计算了所设计的直板式以及5种不同顶部形式的近轨吸声矮墙的插入损失值，分别取6个受声点作为研究对象。结果表明，近轨吸声矮墙对于轨道两侧垂直距离较低的区域，比如行人，拥有更好的保护效果。总的来说，增加顶部形式可以改变近轨吸声矮墙的降噪特性，提升近轨吸声矮墙的降噪能力，且可以增强其降噪的频率针对性。在后期的研究和设计中，可以根据所保护对象不同、线路的噪声频率特点，有针对性地选择不同的顶部形式。

(3)采用边界元法仿真计算近轨吸声矮墙降噪效果时，对于前文所设计的直板式近轨吸声矮墙，对比其仿真计算结果与前文经验公式的计算结果。发现，在400 Hz以下频率段吻合较差，而在高于400 Hz频率段，两种方法的计算结果基本吻合。可以认为在相对较高的频段，比如400 Hz以上频域，利用经验公式法和仿真计算方法来计算近轨吸声矮墙降噪效果(插入损失)其结果均较为可靠；而在较低频域，比如400 Hz以下，噪声的波长较长，与地面不可避免地发生较为复杂的反射吸收等现象。此时还需进一步进行实际试验，得到较为可靠的试验数据，来完善仿真计算的参数可靠性，以获得更为可靠的预测模型。