人类利用质数保护自己
沈叶华

我在上一篇科普小品《质数冥冥中保护着“周期蝉”》(见本刊2019年第2期)谈到一个有趣的生物现象,虽然“周期蝉”天敌无数,但它能从上百万年世世代代活下来,它生存本能的“质数周期法”这个杀手锏功不可没。质数与其他合数、奇数、偶数、整数、自然数、完全数等砌起数学的殿堂,质数更是数学殿堂的特殊石砖。那么,质数特殊在哪里?我们玩个小游戏来看看。
假如我们有7个苹果,怎样把它们摆放开来?我们可以这样摆:
无论怎样,都无法把7个苹果摆整齐,都无法把它们平均地排列(总有一个冒出来),因此我们说:7是质数。但如果我们有1 2个苹果,我们可以这样摆:也可以这样摆:
至少有一种方法能把12个苹果平均地排列,因此我们说:12不是质数,是合数。看明白质数与合数的区别吗?质数是个体,不可平均分割;合数是组合,可以整齐地分切。
因此说,合数是质数与质数的乘积,合数全由质数产生。
2×2×7=28
2×17=34
2×2×2×2× 3= 48
2×2×3×5= 60
5×31=155
2,3,5,7,1 7,3 1不都是质数?28,34,48,60,1 55不都是合数?大家找一找,算一算,有哪一个合数不是数个质数的乘积?
如果将质数、合数比拟为食物,质数像食材,如鸡蛋、猪肉各是一种原材料(质数),鸡蛋不能分解为“鸡”+“蛋”,猪肉不能分解为“猪”+“肉”;相对地,合数像菜式,如鸡蛋饺,就是用鸡蛋浆裹着猪肉末煎炸出来的(合数)。
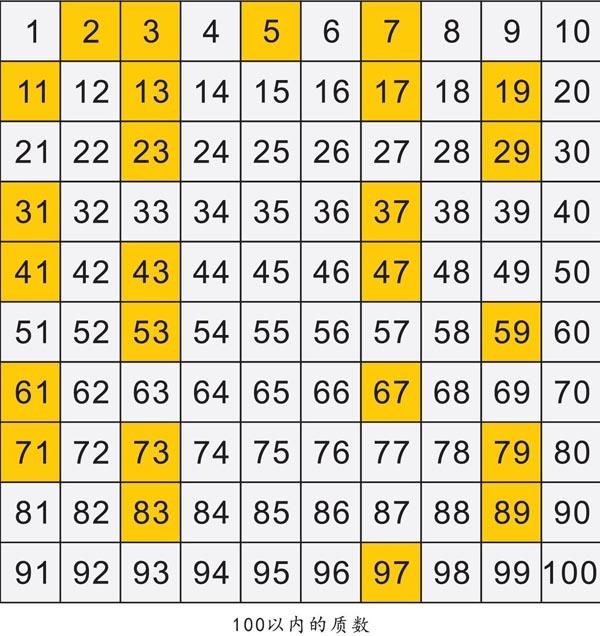
我们知道,奇数、偶数在数轴上排队,一前一后,互相穿插,很有规律。质数藏身数轴中,要找出它,就像在广袤的森林里要找出你所需的树,得一棵棵去找。下圖黄色的为质数,看看:它们有时聚在一块,有时离得远远的,相隔的距离像很随意。
那么,质数在数轴上的分布有规律可循吗?从公元前300年起,人类一直孜孜不倦地寻找质数的分布规律,至今仍未发现。
因此,发现新质数仍是件费时费力的苦差事——即使今天有了电脑,有了互联网,有了搜索质数的专业软件——特别是随着质数趋向无穷大,它们分布得越来越稀疏。
比如,已知的最大质数:2 77232917-1=467 333 183 359 231...730 618 069762 1 79 0 7 1,共有2 3 249 425位,也就是说,如果中间不省略,要写多长?写满9000页纸,约9套《红楼梦》书那么厚。这个质数是一位美国数学发烧友花了14年业余时间,在2018年年初发现的。
人类至今既未发现找质数的快速方法,也未发现整数分解的简捷办法,如此一来,检验一个大数是质数还是合数,就非常费劲了。在1536年,人们以为267-1是质数,直到1903年,才分解出它的因子,证明它是合数:
267-1= 147 573 952 589 676 412 927= 761 838 257 287×1 93 707 72 1
分解267-1足足花了3个多世纪。
质数呀质数,人类研究你已有2 300年,但至今好像仍只看到你的表象,未能完全揭开你的面纱。
人类毕竟是万物之灵,虽对质数的学问还未穷尽,但懂它多少就利用它多少吧,快让它为我们效劳,这没说的。
那就让质数管管我们今天的腰包吧。可能你会说,不懂得质数又如何,还不是一样晓得掏腰包买东西?但当今此言差矣。
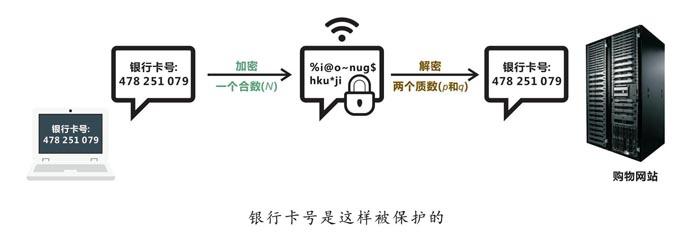
现在我们进行网购,在电脑上输入银行卡号,为什么它不会被黑客盗走?因为经过了电脑的加密与网站的解密。电脑用什么加密,网站用什么解密?两个质数、一个合数:这两个质数的乘积正是这个合数,例如:N =pxq,N是合数,p和q是质数。
我们输入银行卡号,电脑用合数(N)和银行卡号掺合一起,然后发送出去,网站收到这堆混乱信息后,用质数(p和q)进行分解,读出银行卡号。也就是说,必需使用p和q才能分解N,才能解读原信息。这样一来,即使信息在传送途中被黑客盗走,黑客没有p和q,无法分解N,也就无法读取银行卡号。
黑客不会自己动手分解N吗?这就是前面提到的:人类至今未掌握合数分解的简捷办法,仍在使用笨方法。例如:分解合数5609,求出它的两个因子,就没有直接求得的方法,只能从2开始除,5 609÷2=? 5609÷3=? 5609÷5=?……一个个数除上去,一直除到71 (5609÷71=79) 5609才能被整除,才分解出它的两个因子:71和79。
7 1和79不过区区两位,网络加密使用的是数百位、上千位的大质数。为什么是大质数?质数越大,它们被黑客强力分解出来的难度也越高。看看,下面这个合数共617位,是两个质数的乘积,要将它们分解出来?想想就令黑客望而却步了。
这就是保卫着网络通信安全的门神大将:RSA加密算法及其工作原理。RSA加密算法是3位美国数学家在1977年创立的。我们今天之所以能信任互联网:浏览网页,不担心信息被黑客删改;进行网购、电子商务,不操心钱被偷走,资金被转移……多亏了RSA加密算法的严防死守,牢不可破。再细细想:RSA的防守武器不正是利用质数分布的随意性,大质数难以被分解出来这些个大特性吗?

