基于灰色模型的蔬菜农药残留量不确定度评定

程福安 章家岩 冯旭刚 高文斌 钱牧云

(1.安徽工业大学电气与信息工程学院，安徽 马鞍山 243032；2.安徽工业大学机械工程学院，安徽 马鞍山 243032)

农药的使用虽然确保了蔬果的增产，但同时也带来了一系列蔬果污染等负面问题[1-3]。随着蔬果种植条件和气候因素的不断变化，病虫害种类逐年增多，致使过度使用农药，导致农药残留严重超标。近年来，因农药残留超标而引起的中毒事件时有发生。为此，相关政府部门制定的农药残留限量标准日趋严苛，农药残留检测技术也日益完善。但是假如农药残留检测结果准确度不明，其实际意义就会遭受质疑。因此，对农药残留检测结果的准确度进行评定，是蔬果农产品检测中必不可少的一个环节。蔬果农药残留检测数据的不确定度是评判农残量检测结果质量高低的一个重要指标。农残量的不确定度越小，则检测结果与被测量的真值也就越接近。

随着农业科学和计算机技术的发展，众多学者采用气(液)相色谱法对特定食品农药残留量的不确定度评定进行了深入研究[4-6]。崔淑华等[7]使用液相色谱法测定鸡肉中二氯二甲吡啶酚残留量，计算了合成标准不确定度和扩展不确定度。郑怀东等[8]建立气相色谱法测定河蟹中多氯联苯的不确定度评定的数学模型，并对多氯联苯残留量的不确定度进行了评定。潘城等[9]采用高效液相色谱法对蔬菜中异菌脲残留量的不确定度进行评估，并对不确定度分量进行了量化和合成。然而，这些评定方法大多根据以往经验进行假设农药残留检测值的分布类型，并且多采用统计学的方法计算不确定度，其评定速度相对较慢。因此，为解决小样本蔬菜农药残留检测值的统计标准差[10-11]计算速度相对较慢，以及获取检测值的分布类型困难等因素而使得对其不确定度难以准确评定的问题，本研究拟从计量学的角度出发[12-14]，提出一种基于灰色模型的不确定度评定方法，旨在为小样本、分布类型未知的蔬果农残量不确定度的评定提供参考。

1 检测方法及试验步骤

1.1 试剂与仪器

1.1.1 主要试剂

乙腈、正己烷：色谱纯，北京迪马科技有限公司；

丙酮：色谱纯，美国TEDIA公司；

氯化钠：色谱纯，阿拉丁试剂(上海)有限公司；

有机氯农药标准品、拟除虫菊酯类标准品：上海安谱实验科技股份有限公司；

弗罗里硅土柱：美国Agilent公司。

1.1.2 主要仪器与设备

气相色谱仪：GC-2010型，日本岛津公司；

组织捣碎机：FK-A型，常州市金坛区环宇科学仪器厂；

高速匀浆机：FS-1型，常州市金坛区环宇科学仪器厂；

机械振荡器：HY-2A型，常州市金坛区环宇科学仪器厂；

旋转蒸发仪：RV05basic2-B型，德国IKA公司；

氮吹仪：NC-2012型，山东鲁创分析仪器有限公司；

精密电子天平：AR224CN型，奥豪斯仪器(上海)有限公司。

1.2 检测方法

农残样品前处理过程要求在充分提取待测组分的前提下，尽量去除对目标物产生干扰的杂质，以实现下一步的准确检测。前处理过程主要包括提取、分离、净化和浓缩等环节。为此，首先采用乙腈对白菜中的农药成分进行提取，通过匀浆、过滤和浓缩，然后用弗罗里硅土柱进行分离、净化，获得的淋洗液经过浓缩后定容，再将其注入气相色谱仪测定。依据保留时间进行定性，按照标准溶液峰面积和样品溶液峰面积的比值进行定量。

1.3 试验步骤

精确称取25.00 g粉碎均质的待测样品(精确到小数点后两位)置于高型烧杯中，然后加入50 mL乙腈，于高速匀浆机在500 r/min的条件下匀浆2 min后过滤，将滤液转移到装有6 g氯化钠的100 mL具塞量筒中，塞上塞子，剧烈振荡1 min，在25 ℃室温下静置45 min，等待水相和乙腈相充分分层。从具塞量筒中吸取10 mL乙腈提取液，放入25 mL的圆底烧瓶中，在旋转蒸发仪上(55 ℃水浴温度)蒸发近干，加入2 mL正己烷，待净化。依次用5.0 mL 丙酮+正己烷(体积比1∶9)、5.0 mL正己烷对弗罗里硅土柱进行预淋洗，当溶剂液面上升到柱吸附层表面时，立即加入上述待净化溶液，用15 mL刻度离心管接收洗脱液，用5.0 mL丙酮+正己烷(体积比1∶9)冲洗圆底烧瓶后淋洗弗罗里硅土柱，并重复上述操作一次。将装有淋洗液的离心管放置在氮吹仪上，氮吹蒸发至体积<5 mL，并用正己烷准确定容到5 mL。混匀后分别移入2 mL自动进样器样品瓶中，供气相色谱分析。

1.4 农残量计算公式

(1)

式中：

X——试样中9种有机氯和拟除虫菊酯类农残量，mg/L；

V1——提取溶剂的体积，mL；

V2——抽取用于检测的提取溶液的体积，mL；

A——样品溶液中被测农残量的峰面积；

As——农药标准溶液中被测农残量的峰面积；

V3——样品溶液定容体积，mL；

m——称取样品的质量，mg；

c——农药标准液的质量浓度，mg/L。

2 农残量不确定度的灰色评定建模

2.1 理想的农药残留量检测过程

对于理想的农药残留重复检测过程，每一次检测值都是被测农残量的真实值，不存在检测误差(如图1直线L1)。则理想农药残留检测值数列为：

X(0)={x(0)(i),i=1,2,……,n}，

(2)

式中：

x(0)(i)——理想农残量检测值[x(0)(i)=d]，mg/L；

d——被测农残量的真值，mg/L；

n——农残量检测总次数；

i——第i次检测。

逐次计算式(2)数列X(0)的前n项和，得到理想的农残量累加数列X(1)：

X(1)={x(1)(i),i=1,2,……,n}={d,2d,……,nd}。

(3)

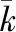
图1 原始检测序列Figure 1 Original detection sequence

(4)

由于不存在检测误差，则理论的农药残留检测过程是一条经过原点(0,0)的直线S1，如图2所示。

2.2 实际的农药残留量检测过程

在实际的农药残留重复检测过程中，由于环境和检测方法等各种影响因素的存在，导致检测值存在误差，使得每一次的农药残留检测值都接近于真实值，且在真实值上下波动(如图1曲线L2)。将农残量检测值中的离群值剔除后，按从小到大的顺序排列，可以得到实际农药残留检测值数列：

Y(0)={y(0)(i),i=1,2,……,n}={d+δ(i),i=1,2,……,n}，

(5)

式中：

y(0)(i)——实际农残量检测值，mg/L；

δ(i)——检测误差，mg/L；

其中：y(0)(i)≤y(0)(i+1)，δ(i)≤δ(i+1)。

逐次计算式(5)数列Y(0)的前n项和，得到实际的农残量累加数列Y(1)：

Y(1)={y(1)(i),i=1,2,……,n}={y(0)(1),y(0)(1)+y(0)(2),……,y(0)(1)+y(0)(2)+……+y(0)(n)}={d+δ(1),2d+δ(1)+δ(2),……,nd+δ(1)+δ(2)+……+δ(n)}。

(6)

如果将农药残留检测次数i作为横坐标，将前n项和y(1)(i)作为纵坐标作图，可得y(1)(i)-i曲线S2，如图2所示。

2.3 检测分散性及不确定度

在图2中，直线S1和曲线S2沿纵坐标轴方向上的差异Δ(i)，直观地反映了蔬菜农残量重复检测时由于各种误差因素的存在产生的被检测值的分散性，根据式(4)和式(6)可得：

图2 累加检测序列Figure 2 Cumulative detection sequence

(7)

通常以最大距离Δmax表示理想农药残留检测过程与实际农药残留检测过程的分散性：

Δmax=max[Δ(i),i=1,2,……,n]。

(8)

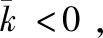
则式(8)可转化为：

(9)

一般地，最大距离Δmax越大，蔬菜农药残留检测数据越分散，相应的标准差越大，其不确定度也越大。

定义灰色标准差SGrey，SGrey表示蔬菜农药残留检测数据的分散程度：

(10)

式中：

c——灰色系数。

研究[15]表明，农残量的分布类型与灰色系数c的相关性较小。通常灰色系数c为2.5。可用灰色标准差近似代替蔬菜农药残留量不确定度：

(11)

3 蔬菜农药残留量不确定度的评定

3.1 蔬菜中9种农药残留量的测定

通过气相色谱法进行6次重复测定试验并根据式(1)，可以得到9种有机氯类和拟除虫菊酯类农药残留量的测定数据，检测结果从小到大排序，结果如表1所示。

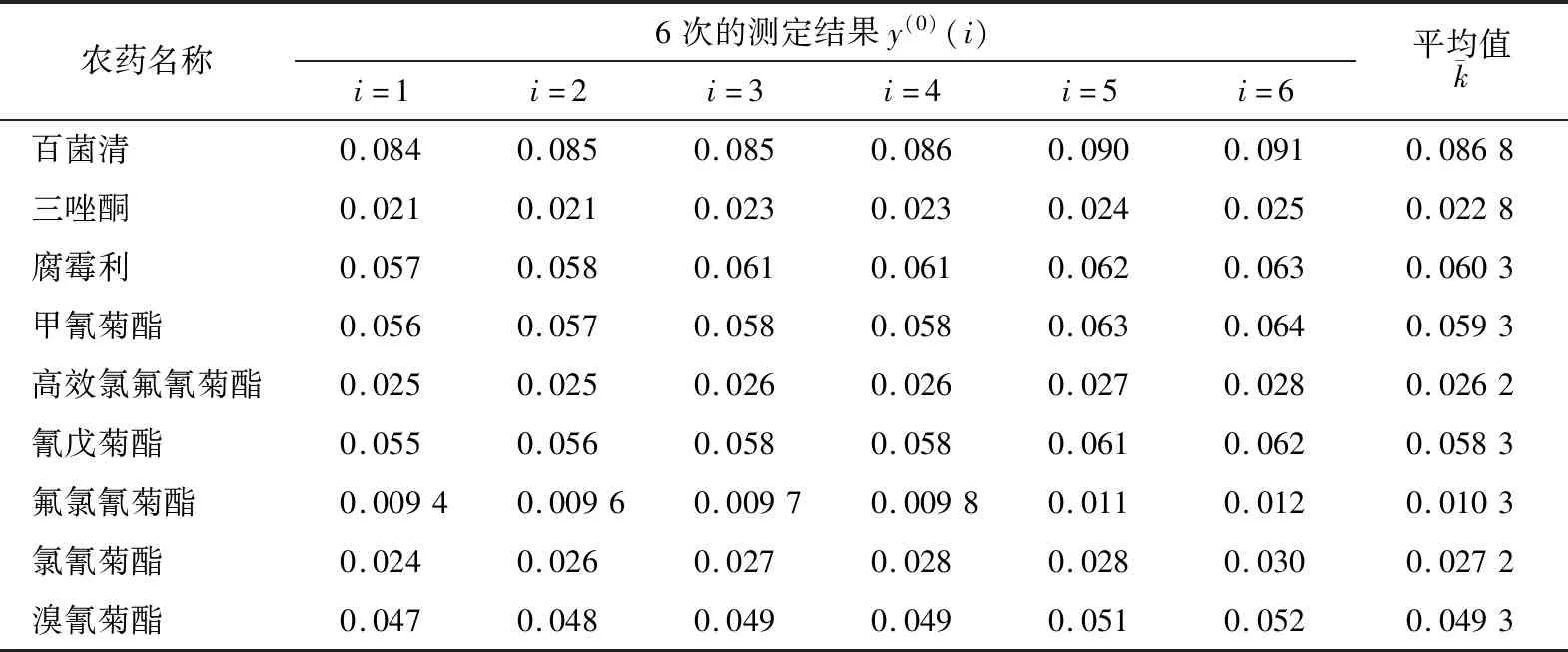
表1 9种农药的测定数据Table 1 Measurement data of nine pesticides mg/L

3.2 百菌清农药检测值不确定度的灰色计算

以农药百菌清为例，采用灰色模型评定方法求其不确定度。

表格2呈现了Δmax计算的具体过程，然而步骤稍显繁杂。通常在蔬菜农残量平均值计算出以后，相应的直接寻找小于平均值的全部检测值，并根据式(9)计算Δmax。

不难发现在计算百菌清农药的Δmax时，仅使用了小于平均值的4次测定值，表明基于灰色模型的评定方法能够较快地评定小样本蔬菜农残量的不确定度。

3.3 9种农药检测值不确定度的评定与比较

3.3.1 农残量不确定度的灰色评定 根据百菌清农药检测值不确定度的灰色评定步骤，采用灰色模型评定方法分别对9种有机氯类和拟除虫菊酯类蔬菜农残量不确定度进行评定，结果见表3。

表2百菌清农药检测值不确定度的灰色计算
Table 2Grey calculation of uncertainty of detection value of chlorothalonil pesticide

mg/L

表39种农药检测值的不确定度灰色评定结果
Table 3Grey evaluation results of uncertainty of nine pesticide detection values

mg/L

3.3.2 农残量不确定度的统计评定 蔬菜农残量不确定度的统计评定方法，主要是根据式(12)、(13)和(14)计算农药残留标准差以表征其不确定度。

算术平均值：

(12)

残余误差：

(13)

农药残留检测值的标准差：

(14)

式中：

n——蔬菜农药残留量试验测定次数；

SBessel——农药残留量试验数据的标准差，mg/L。

采用上述统计学方法计算9种有机氯类和拟除虫菊酯类蔬菜农残量的标准差，结果见表4。

表4 9种农药检测值的标准差Table 4 Standard deviation of nine pesticide detection values mg/L

3.3.3 两种评定结果比较 根据表3和表4的评定结果进行绘制对比曲线图，如图3所示。利用Pearson相关系数公式可计算得到两条曲线的相关系数为0.997，表明采用灰色模型对9种有机氯类和拟除虫菊酯类农药的不确定度评定值和统计标准差的计算值之间无显著性差异。

综上，基于灰色模型的评定方法具有一定的可行性，可用于蔬菜农药残留量的不确定度评定。

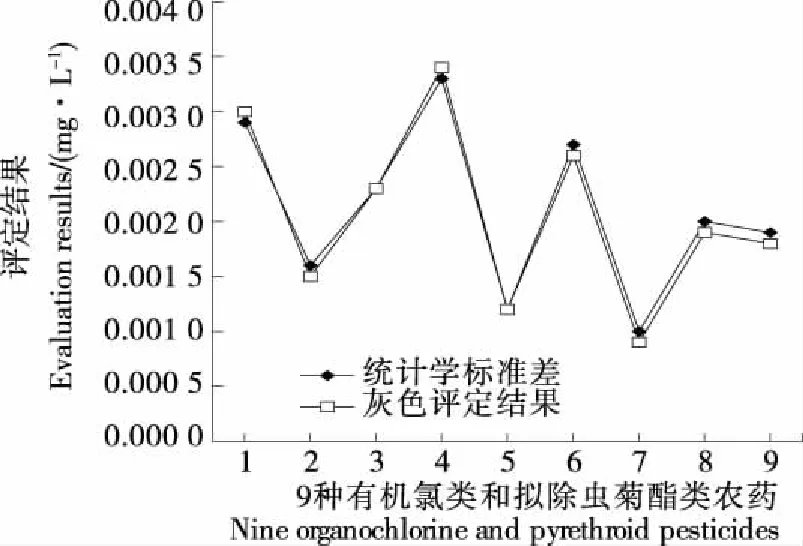
1.百菌清 2.三唑酮 3.腐霉利 4.甲氰菊酯 5.高效氯氟氰菊酯 6.氯氟菊酯 7.氯氰菊酯 8.氰戊菊酯 9.溴氰菊酯
图3 两种评定方法的结果对比
Figure 3 Comparison of the results of the two assessment methods

4 结论

本研究基于计量技术提出了蔬菜农残量不确定度的灰色模型评定方法，对9种有机氯类和拟除虫菊酯类农药的不确定度进行了评定，结果表明：蔬菜农残量不确定度的灰色评定值与统计学标准差计算值之间无显著性差异，两者相关系数为0.997。验证了灰色模型在评定蔬菜农残量的不确定度问题上是科学可行的。这种基于灰色模型的评定方法，解决了小样本、检测值的分布函数未知时蔬菜农残量不确定度的评定难题。通过对比评定过程可以发现，基于灰色模型的评定方法比前人给出的统计学方法计算速度更快。此外，通过其他先验信息和试验手段对检测过程的不确定度来源信息进行深入研究，可以合理有据地缩小检测结果的不确定度，进一步提升评定方法的应用价值，这将是后续的研究工作。